Рис.1.48. Трехмерный график

Для практики, решим уравнение ∂²u/∂x²+∂²u/∂y²=-x-y в области G(-1≤x≤1; -1≤y≤1) при u(x,y)=0 на границе области. Построим область, в которой будем искать решение.

Затем, помня что канонический вид уравнения A(x,y)∂²u/∂x² + 2B(x,y)∂²u/∂x∂y + C(x,y)∂²u/∂y² + D(x,y)∂u/∂x + E(x,y)∂u/∂y + G(x,y)u = F(x,y), и посмотрев повнимательней на то уравнение, которое решаем, приходим к выводу, что коэффициенты A=1, B=0, C=1, D=0, E=0, G=0, F=x+y, а само уравнение эллиптическое, так как В²-АС<0.

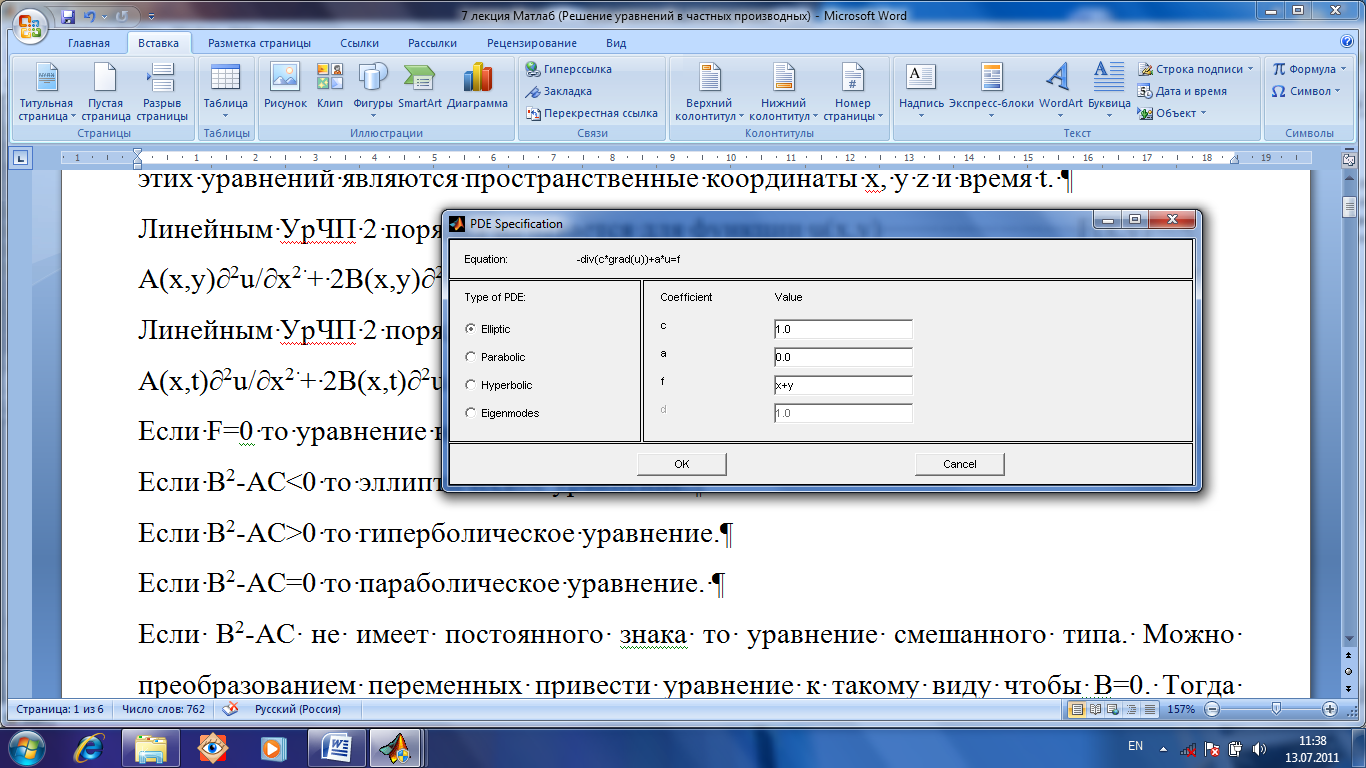
Вводим в окне PDE Specification значения (Рис.1.49) коэффициентов.

Рис.1.49. Вводим в окне PDE Specification значения коэффициентов.

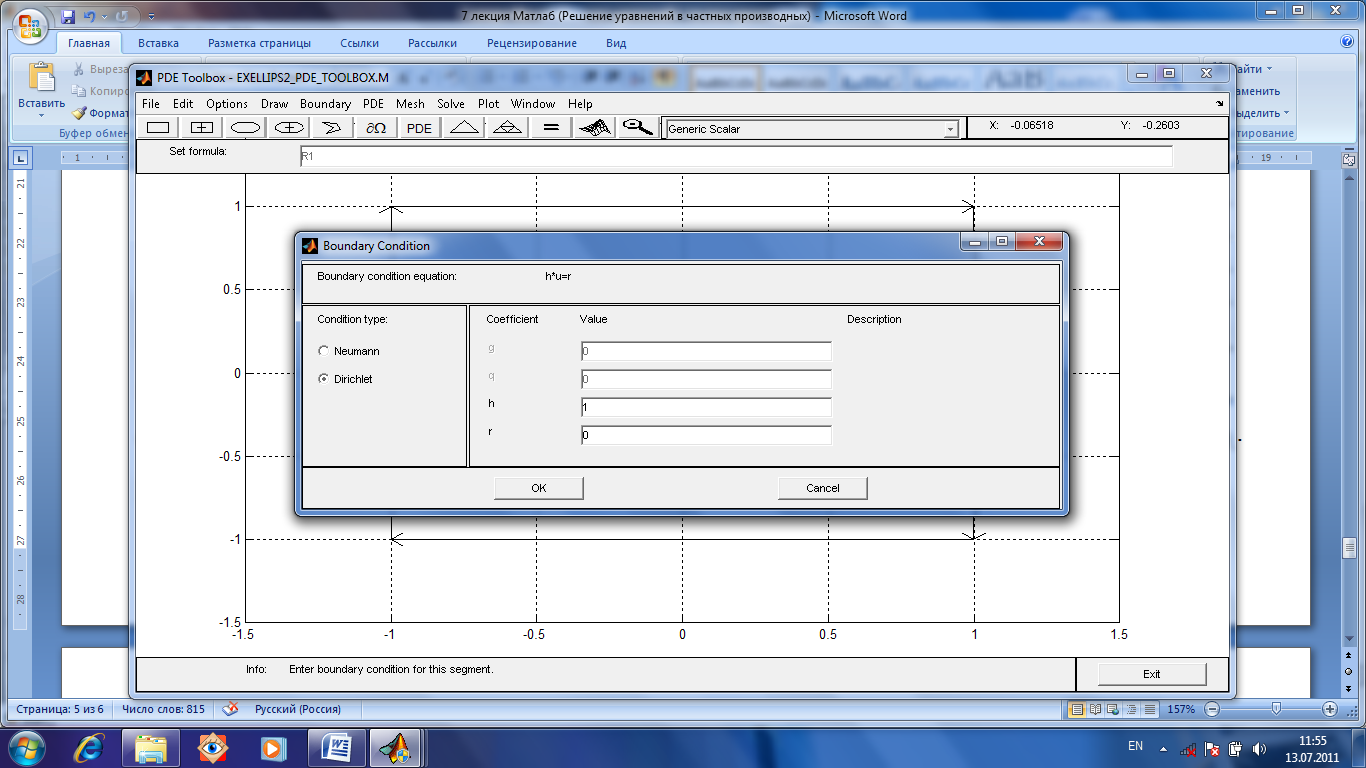
Затем выделить стороны (границы области) и определим на них граничные условия. Зная что u(x,y)=0 на границе области, введем соответствующие значения коэффициентов в окне Boundary Condition (рис.1.50).

После этого произвести триангуляцию области.

Затем запустить расчеты и получить график решения.

Отредактировать его хорошенько, повернуть поудобнее, наложить сетку и так далее.

Рис.1.50. Введем соответствующие значения коэффициентов в окне Boundary Condition

Решение нестационарных задач (гиперболических и параболических уравнений). Рассмотрим задачу о колебаниях прямоугольной мембраны (Рис.1.51, Рис.1.52, Рис.1.53). Уравнение ее колебаний имеет вид ∂²u/∂t²=a²(∂²u/∂x²+∂²u/∂y²) при условиях u(0,y,t)=u(l₁,y,t)=u(x,0,t)=u(x,l₂,t)=0, а также при u(x,y,0)=Axy(l₁-x)(l₂-y), и при u_t(x,y,0)=0. Пусть например l₁=2, l₂=3, A=1, a=2.

Рис.1.51. Рассмотрим задачу о колебаниях прямоугольной мембраны

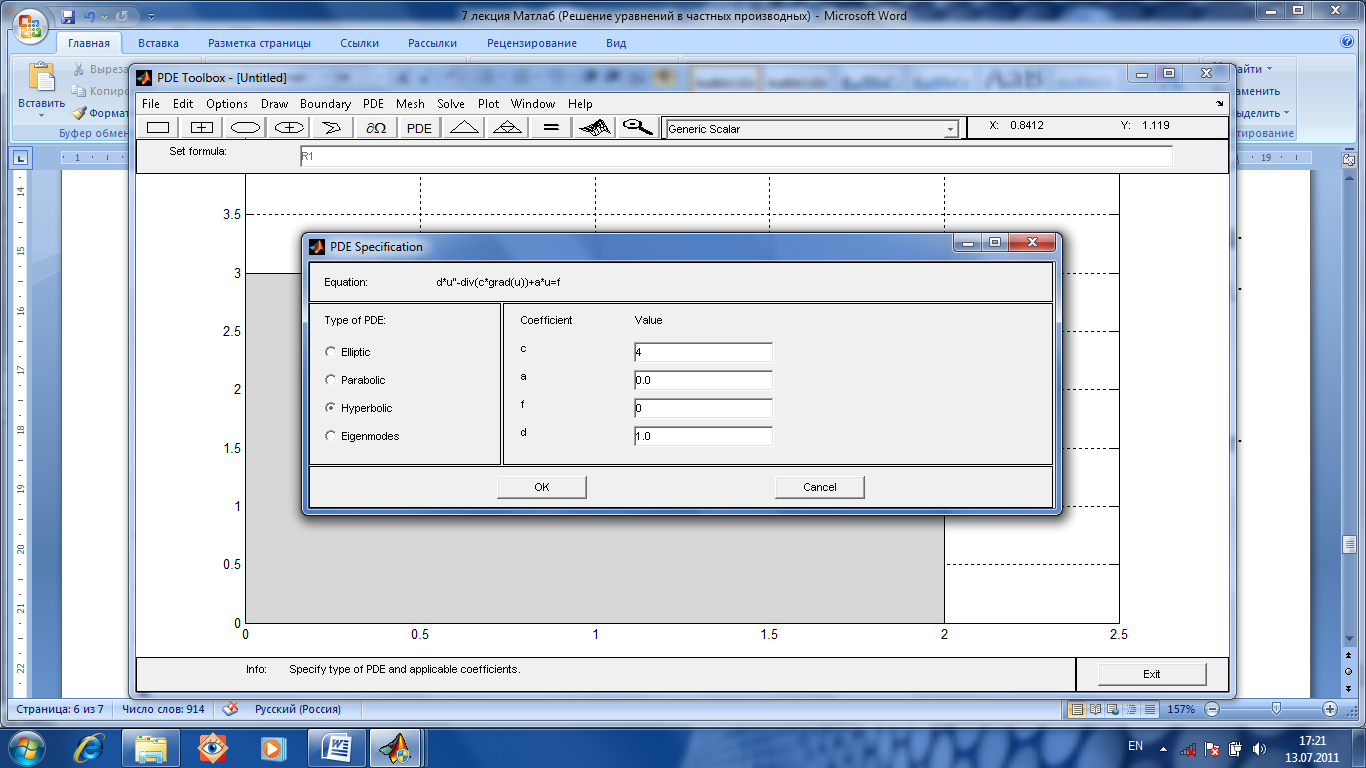
Зададим область решения по х(0, 2) и по у(0, 3). Затем определяем гиперболическое уравнение и его коэффициенты.

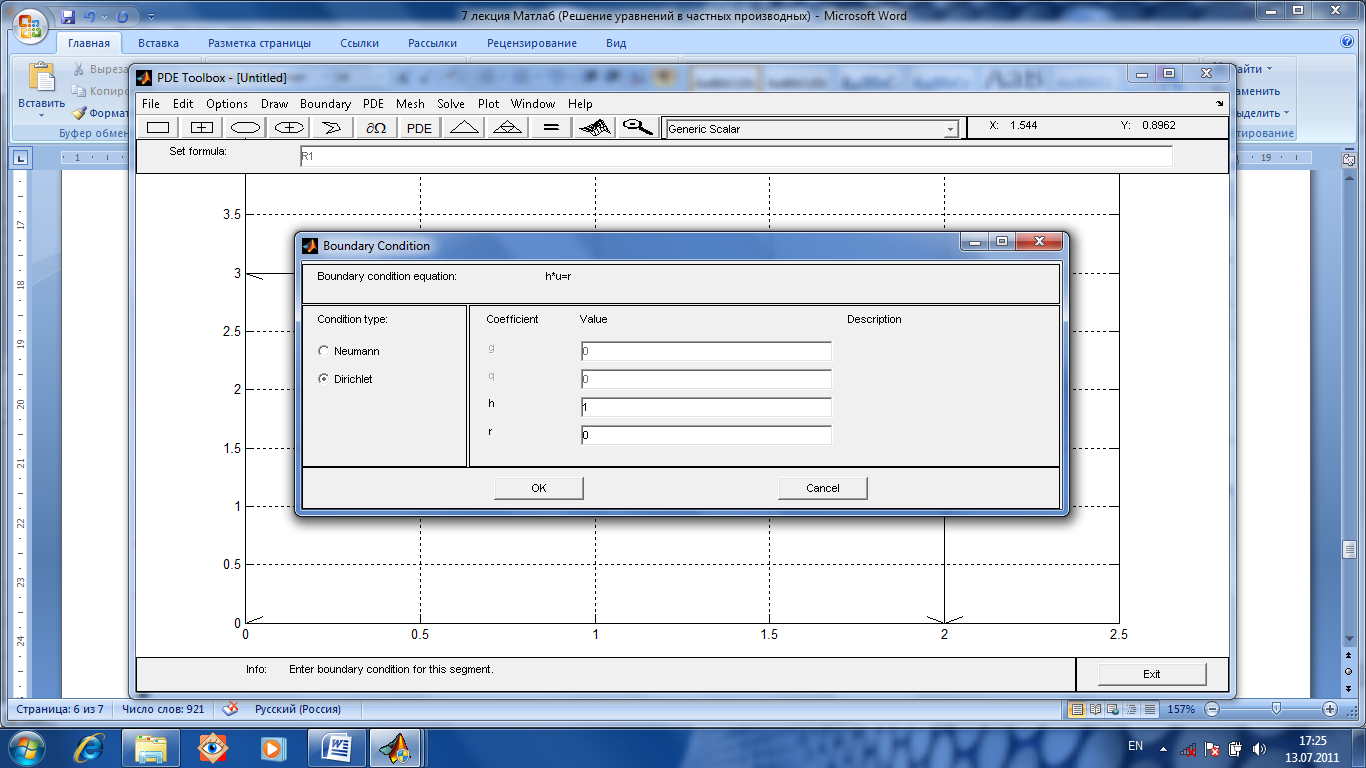
После этого определяем нулевые условия на границе (рис.1.52)

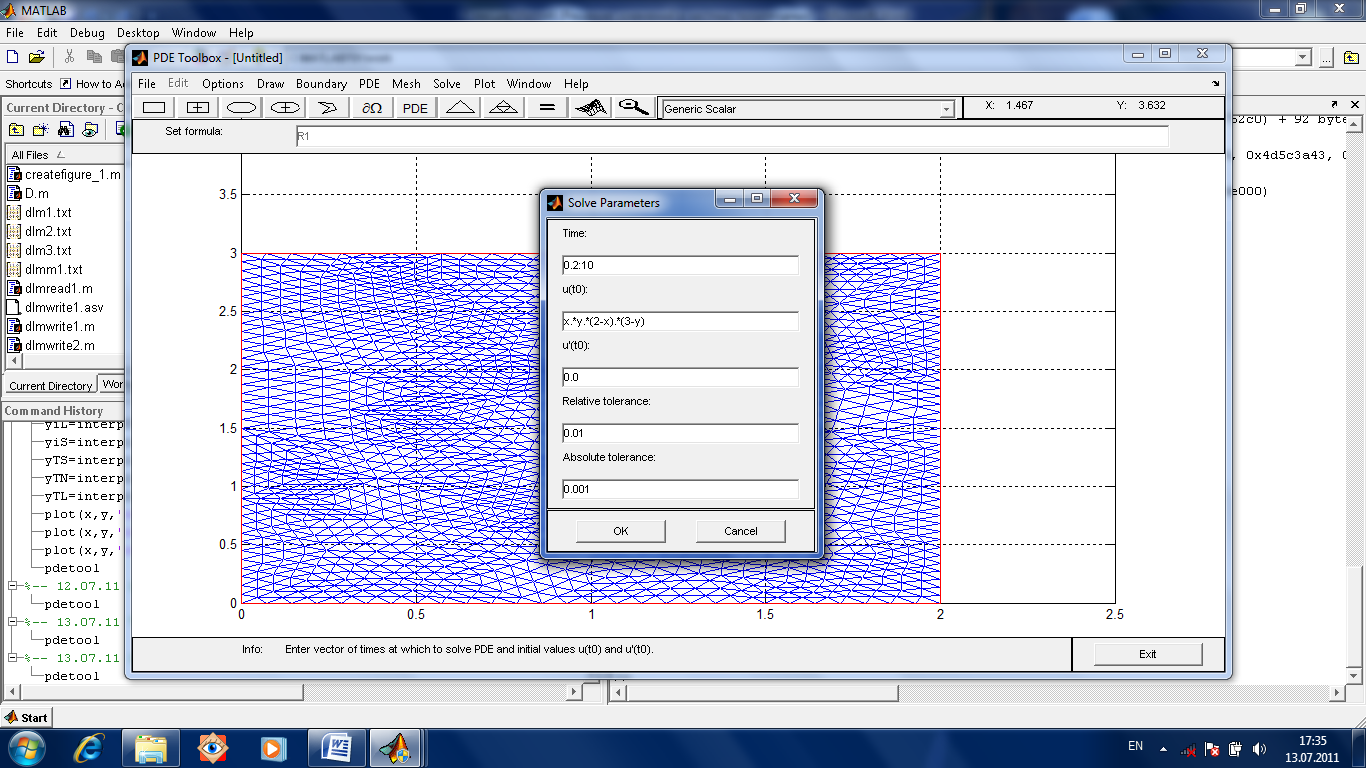
В отличие от рассмотренных ранее эллиптических уравнений, необходимо определить интервал изменения времени, начальные условия и точность решения. Для этого есть пункт меню Solve-Solve Parameters.