2020-10-10
148
f=inline(‘<функция>');
x=a:h:b;
plot(x,f(x),'k-')
Площадь S можно вычислить как сумму элементарных площадей определенных для соответствующих элементарных отрезков длиной h: S = s0+s1+s2+…si+…..+sn–1 Произвольную площадь si можно вычислить, как определенный интеграл на отрезке [xi;xi+1] от более простой функции φi(x), которой заменим реальную функцию f(x): 
Вид функции φi(x) будет определять название метода.
Методы прямоугольников. Значение функции φi(x) на отрезке [xi;xi+1] принимается константой
Метод прямоугольников вперед. Для функции φi(x) = yi значения элементарной si и общей S площади можно вычислить как: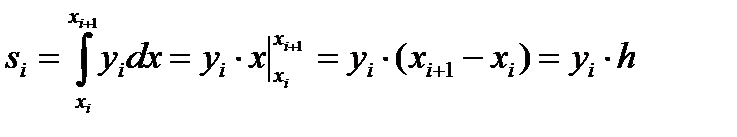 
, тогда 
x=a:h:b-h;
S=h*sum(f(x));
Метод прямоугольников назад. Для функции φi(x) = yi значения элементарной si и общей S площади можно вычислить как: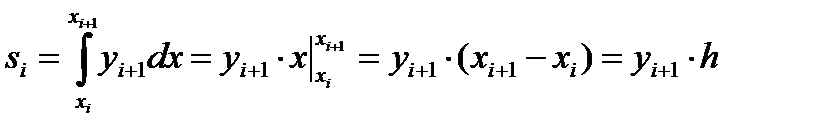 
, тогда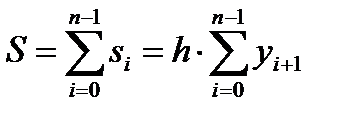 
x=a+h:h:b;
S=h*sum(f(x));
Метод прямоугольников в среднем. Вычислим 
и значение функции 
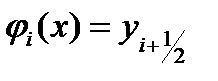Тогда значения элементарной si и общей S площади можно вычислить как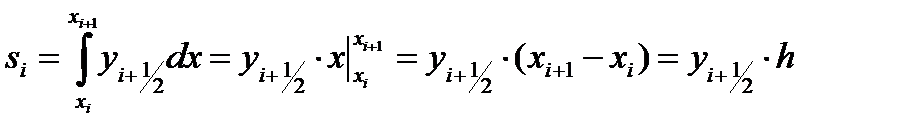 
x=a+h/2:h:b;
S=h*sum(f(x));
Метод трапеций. Функцию φi(x) будем определять как линейную на отрезке [xi;xi+1], т.е. ее график должен проходить через две смежные точки (xi,yi) и (xi+1,yi+1). Функцию φi(x) можно будет представить как интерполяционный многочлен Лагранжа, построенный по двум точкам (xi,yi) и (xi+1,yi+1): 
тогда значения элементарной si площади можно вычислить как: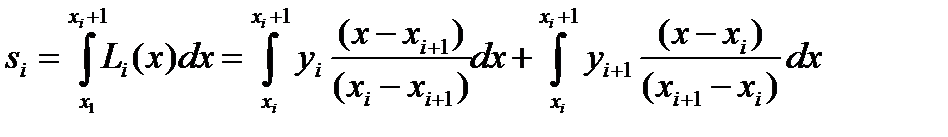 
Введем переменную 
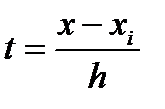Тогда x = xi + h·t и dx = h·dt. Значениям x, равным x, xi+1 соответствуют значения t, равные 0, 1. Значение (x-xi) = xi–xi + h·t = h·t. Значение (x-xi+1) = xi – xi+1+ h·t = h(t-1). Элементарную площадь si с использованием новой переменной определим как:
|
|
|
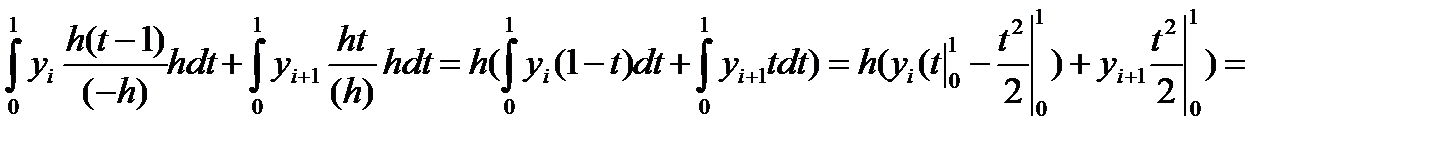
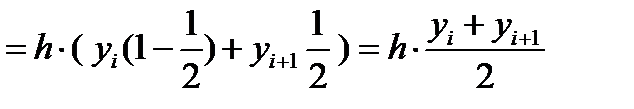
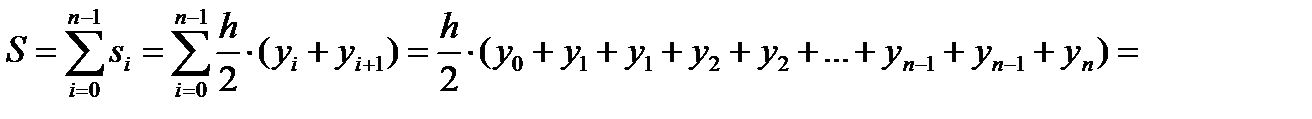
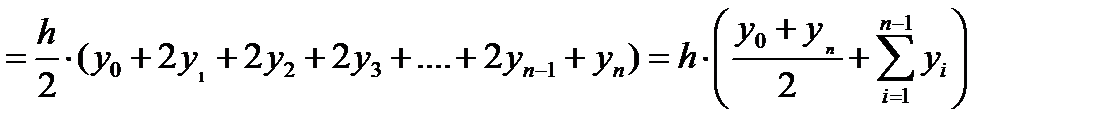
| x=a:h:b-h; S=h*sum((f(x)+f(x+h))/2); | x=a:h:b; S=trapz(x,f(x)); | x=a:h:b; S=h*trapz(f(x)); |
Метод Симпсона. Определим точку xi+½ = xi+½·h в середине элементарного отрезка [xi;xi+1] и значение функции в этой точке yi+½ Функцию φi(x) будем определять как квадратичную на отрезке [xi;xi+1], т.е. её график должен проходить через три смежные точки (xi,yi),(xi+½ , yi+½) и (xi+1,yi+1). Функцию φi(x) можно будет представить как интерполяционный многочлен Лагранжа, построенный по трём точкам xi, xi+½ и xi+1:
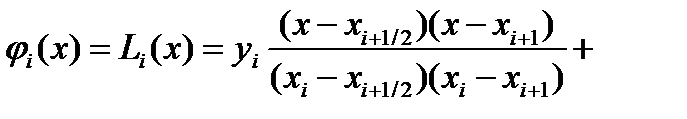
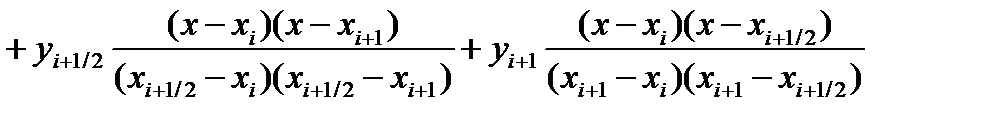Тогда значения элементарной si площади можно вычислить как:
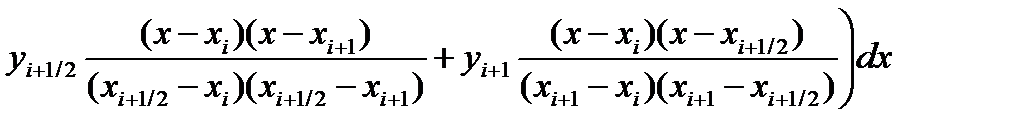Введем переменную 
тогда x = xi + h·t и dx = h·dt. Значениям x, равным xi, xi+½, xi+1 соответствуют значения t, равные 0,½,1 Значение (x-xi) = xi–xi + h·t = h·t. Значение (x-xi+½) = xi – xi+½ + h·t = h(t- ½) Значение (x-xi+1) = xi – xi+1+ h·t = h(t-1) Элементарную площадь si с использование новой переменной определим как:
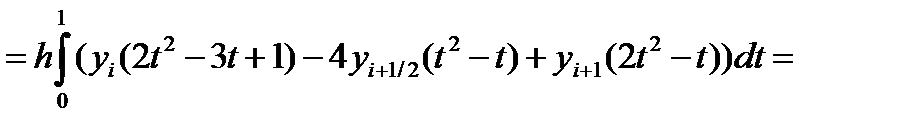
Тогда значения общей S площади можно вычислить как:
| x=a+h:h:b-h; xs=a+h/2:h:b; S=h/6*(f(a)+f(b)+2*sum(f(x))+4*sum(f(xs))); | S=quad(f,a,b); |
Программа. Интегрирование. Сравнение погрешностей методов при одинаковом числе шагов
function DATA
global a b n;
a=-1;
b=4;
n=50;
end
function [ fx ] = f(x)
|
|
|
fx=x.^2-5;
end
function [ Integr ] = Pramougoln_Vpered(a,b,n)
disp('Pramougoln_Vpered');
h=(b-a)/n;
for i=1:n+1
if i==1
x(i)=a;
else
x(i)=x(i-1)+h;
end%if
y(i)=f(x(i));
end%for i
sum=0;
for i=1:n
sum=sum+y(i);
end%for i
Integr=h*sum;
end
function [ Integr ] = Pramougoln_Nazad(a,b,n)
disp('Pramougoln_Nazad');
h=(b-a)/n;
for i=1:n+1
if i==1
x(i)=a;
else
x(i)=x(i-1)+h;
end%if
y(i)=f(x(i));
end%for i
sum=0;
for i=2:n+1
sum=sum+y(i);
end%for i
Integr=h*sum;
end
function [ Integr ] = Pramougoln_Sredn(a,b,n)
disp('Pramougoln_Sredn');
h=(b-a)/n;
for i=1:n
if i==1
x(i)=a+h/2;
else
x(i)=x(i-1)+h;
end%if
y(i)=f(x(i));
end%for i
sum=0;
for i=1:n
sum=sum+y(i);
end%for i
Integr=h*sum;
end
function [ Integr ] = Trapez(a,b,n)
disp('Trapez');
h=(b-a)/n;
for i=1:n+1
if i==1
x(i)=a;
else
x(i)=x(i-1)+h;
end%if
y(i)=f(x(i));
end%for i
sum=0;
sum=(y(1)+y(n+1))/2;
for i=2:n
sum=sum+y(i);
end%for i
Integr=h*sum;
end
function [ Integr ] = Symps(a,b,n)
disp('Symps');
h=(b-a)/n;
for i=1:n+1
if i==1
x(i)=a;
else
x(i)=x(i-1)+h;
end%if
y(i)=f(x(i));
end%for i
for i=1:n
if i==1
xsr(i)=a+h/2;
else
xsr(i)=xsr(i-1)+h;
end%if
ysr(i)=f(xsr(i));
end%for i
sum=0;
for i=1:n
sum=sum+y(i)+4*ysr(i)+y(i+1);
end%for i
Integr=h*sum/6;
end
function GLAV_Integr
global a b n Integral;
DATA;
[ Integral(1) ] = Pramougoln_Vpered(a,b,n);
[ Integral(2) ] = Pramougoln_Nazad(a,b,n);
[ Integral(3) ] = Pramougoln_Sredn(a,b,n);
[ Integral(4) ] = Trapez(a,b,n);
[ Integral(5) ] = Symps(a,b,n);
REPORT;
end
function REPORT
global a b n Integral;
disp('Arguments f(x)=x^2-5');
disp(['left board a = ' num2str(a,'%10.5f') ]);
disp(['right board b = ' num2str(b,'%10.5f') ]);
disp(['Number of steps n = ' num2str(n,'%10.5f') ]);
disp(['Pramougoln_Vpered = ' num2str(Integral(1),'%10.5f') ]);
disp(['Pramougoln_Nazad = ' num2str(Integral(2),'%10.5f') ]);
disp(['Pramougoln_Sredn = ' num2str(Integral(3),'%10.5f') ]);
disp(['Trapez = ' num2str(Integral(4),'%10.5f') ]);
disp(['Symps = ' num2str(Integral(5),'%10.5f') ]);
end
