Выведите формулу Тейлора с остаточным членом в форме Лагранжа

36. Выведите формулу Тейлора с остаточным членом в форме Лагранжа.

37. Выведите формулу Тейлора с остаточным членом в форме Пеано.

38. Выведите формулу Маклорена для функции y= exс остаточным членом

в форме Лагранжа.

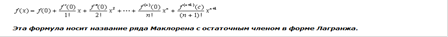
39. Выведите формулу Маклорена для функции y= sin x с остаточным

членом в форме Лагранжа.

40. Выведите формулу Маклорена для функции y= cosxс остаточным

Членом в форме Лагранжа.

41. Выведите формулу Маклорена для функции y= ln(1 + x) с остаточным

Членом в форме Лагранжа.

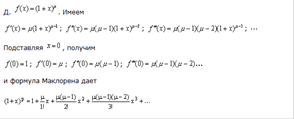
42. Выведите формулу Маклорена для функции y= (1 + x)μс остаточным

Членом в форме Лагранжа.

Сформулируйте и докажите необходимое и достаточное условие

неубывания дифференцируемой функции.

 

Из условия монотонности функции следует, что f(x) не убывает наІ. Пусть

Сформулируйте и докажите необходимое и достаточное условие

Невозрастания дифференцируемой функции.

Теорема (необходимое и достаточное словия убывания дифференцируемой

функции на промежутке). Пусть функция непрерывна на промежутке I и

дифференцируема вовсех его точках, за исключением, может быть конечного их

числа. Если производная f’(x) отрицательна всюду где определена и не равна

тождественно 0 ни на одном интервале I1 принадлежащем I, то функция убывает на I

Из условия монотонности функции следует, что f(x) убывает на І. Пустьдля

некоторых точек х1 и х2, x1<x2, этого промежутка f(x1)=f(x2). Тогда для любой

точки х𝜖(х1,х2) имеем f(x1)≥f(x)≥(x2). Это означает, что функция постоянна на

(х1,х2), и следовательно, f’(x) тождественно равна 0 на этом интервале, что

противоречит условию теоремы. Таким образомf(x1)≠f(x2), а тогда f(x1)>f(x2)и

функция возрастает на I. Теорема доказана.

45. Сформулируйте и докажите достаточное условие возрастания

Дифференцируемой функции.

 

Из условия монотонности функции следует, что f(x) не убывает наІ. Пусть