Пример БД, обладающей свойством соединения без потерь

R =(A, B, C)

ρ =(AB, AC)=(R 1, R 2)

F =(A → B)

Возьмём тот же экземпляр:

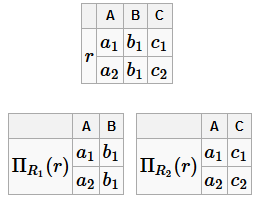
Полученное соединение будет равняться r:

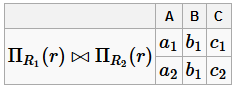
Но это не доказательство, а только один пример, просто чтобы показать, в чём разница.

Алгоритм проверки схемы БД на свойство соединения без потерь

ρ =(R 1... Rn)

R =(A 1... An)

1) построить таблицу T:

И заполнить таблицу T по правилу: если Aj ∈ Ri, то Tij = a, иначе Tij = bi

2) изменить таблицу T - циклически просматривать ФЗ из F в любом порядке, и для очередной ФЗ X → Y ∈ F выполнить следующие действия:

• найти в таблице T строки, совпадающие по атрибутам X (по левой части);
• если хотя бы в одной такой строке значение атрибута Am ∈ Y = a, то во всех найденных строках присвоить Am = a, иначе присвоить Am = bi (i - номер одной из найденных строк), bi должно быть одинаково во всех указанных строках);
• выполнить предыдущие два пункта для всех атрибутов Al ∈ Y;
• выполнить предыдущие три пункта для всех ФЗ из F, циклически их просматривая.

3) алгоритм останавливается, если при очередном просмотре ФЗ из F:

• не произошло никаких изменений в таблице T;
• какая-нибудь строка в T не стала состоять сплошь из символов a (наличие такой строки и говорит о выполнении свойства соединения без потерь).

Пример

Пусть R =(A, B, C)

ρ =(AB, AC)=(R 1, R 2)

F =(A → B)

Доказать, что ρ обладает свойством соединения без потерь.

1)

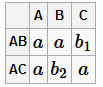
2)

Получили строку, сплошь состоящую из a. Значит ρ обладает свойством соединения без потерь.

Другой пример

Пусть R =(A, B, C, D, E, F, P, S)

ρ =(AB, ACDPS, BCPS, DEF)=(R 1, R 2, R 3, R 4)

F =(B → C, D → EF, B → PS, A → CDPS, AP → S)

Доказать, что ρ обладает свойством соединения без потерь.

1)

2)

первый просмотр:

второй просмотр:

Вот и получили строку, сплошь состоящую из a. Значит ρ обладает свойством соединения без потерь.

 

Лекция №4 - Хорошая схема БД - Сохранение ФЗ

 

Свойства "хорошей" схемы БД

Соединение без потерь

Теорема о свойстве соединения без потерь

Пусть ρ =(R 1, R 2) и F - множество ФЗ.

ρ обладает свойством соединения без потерь тогда и только тогда, когда выполняется хотя бы одно из:

• R 1⋂ R 2→ R 1− R 2 (1)
• R 1⋂ R 2→ R 2− R 1 (2)

Доказательство

1)

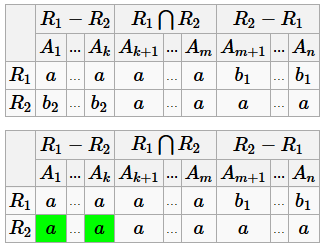
Получили строку, сплошь состоящую из a.

2)

Теперь докажем обратное, что если ρ обладает соединением без потерь, то имеет место одна из ФЗ: (1) или (2).

r =Π R 1(r)⋈Π R 2(r) (3)

r - это R 1⋃ R 2 (экземпляр универсальной схемы отношений)

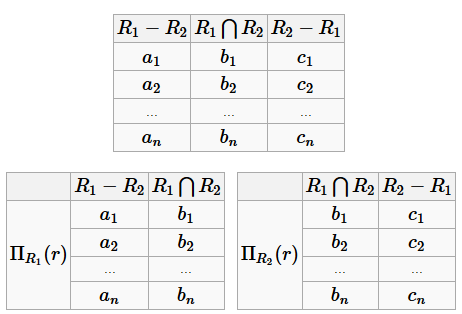
Если выполняется равенство (3), то возможны два варианта:

1) bi ≠ bj, i ≠ j;

2) некоторые bi совпадают, b 1= b 2.

Тогда для выполнения равенства (3) необходимо, чтобы выполнялось одно из двух:

· a 1= a 2;

· c 1= c 2.

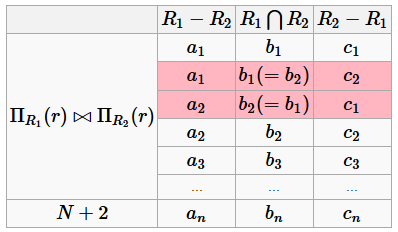
2 и 3 кортежи - лишние. Чтобы они не были лишними, они должны совпадать с одним из других кортежей, чтобы их можно было вычеркнуть.

Предположим, a 1= a 2, тогда что-то там насовпадало и 2 и 3 кортежи можно вычеркнуть.

Аналогичные рассуждения можно провести для случая, когда c 1= c 2, но тогда получаем:

· для варианта bi ≠ bj имеют место обе ФЗ: (1) и (2);

· для варианта с некоторыми совпадающими bi работает либо (1), либо (2).

Всё, теорема доказана.

Следствие из теоремы

Пусть R 1 и R 2 - это сущности БД и они связаны между собой. Тогда схема БД обладает соединением без потерь, если общий атрибут R 1 и R 2 содержит ключ одной из этих схем отношений.

R 1⋂ R 2= A

R 1− R 2= B

R 1⋂ R 2→ R 1− R 2, потому что A → B, так как является ключом.