Функциональные зависимости

Пусть R =(A 1... An) является функциональной схемой отношения и X, Y - некоторые подмножества атрибутов этой схемы. Говорят, что X функционально определяет Y (X → Y), если в любом экземпляре отношения со схемой R не существует двух кортежей, совпадающих по подмножеству X и не совпадающих по подмножеству Y

Иначе говоря, если два кортежа совпадают по X, то они должны совпадать и по Y

Например, R =(A 1, A 2, A 3, A 4), есть зависимости:

A 1→ A 2 (1)
A 1 A 3→ A 4 (2)

Предположим, что имеет место один экземпляр отношения со схемой R

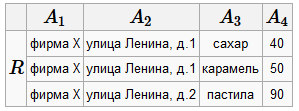
Вторая ФЗ (2) имеет место быть, так как нет двух кортежей, совпадающих по этой паре (по крайней мере, в приведённом экземпляре схемы отношения, а других мы не знаем).

А первая ФЗ (1) не имеет место быть (в третьей строке другой номер дома портит всю картину).

Замыкание множества функциональных зависимостей

Пусть R - универсальная схема отношения, а F - исходное множество функциональных зависимостей на этой схеме. Замыканием F называется всё множество функциональных зависимостей, которое логически следует из F - обозначается как F +

Функциональная зависимость логически следует из F, если её можно вывести (получить) с помощью аксиом Армстронга.

Аксиомы Армстронга

Или правила вывода функциональной зависимости. Существуют различные интерпретации аксиом, но все эквивалентны. Потому приведём только один вариант.

Аксиомы Армстронга являются надёжными и полными.

Надёжность - если ФЗ выводится с помощью аксиом Армстронга, то она справедлива во всех экземплярах отношения, где справедливы исходные ФЗ F

Полнота - если имеет место какая-либо ФЗ, то она обязательно может быть выведена с помощью аксиом Армстронга.

Рефлексивность

Если Y ⊆ X ⊆ R

то X → Y. Тривиальная аксиома.

Дополнение

Если X → Y и Z ⊆ R (Z может быть пустым),

тогда X ⋃ Z → Y ⋃ Z или XZ → YZ

Транзитивность

Если X → Y, а Y → Z,

то X → Z

Пример построения множества ФЗ

Пусть задана УСО (универсальная схема отношения) R =(A, B, C) и зависимости F =(A → B, B → C)

A → A, B → B, C → C, AB → A, AB → B, AC → A, AC → C, BC → B, BC → C, ABC → A, ABC → C, AB → AB, AC → AC, BC → BC, ABC → AB, ABC → AC, ABC → BC, ABC → ABC
A → AB (1ФЗ и пополняем A), AC → BC, B → BC (2 ФЗ и пополняем B), AB → AC, AC → ABC, AB → ABC, AB → BC, A → AC
A → C (1 и 2 ФЗ), A → ABC

Всё, замыкание (F +) построено. Все перечисленные зависимости образуют замыкание.

Лемма

Справедливы следующие правила. Для их доказательства необходимо пополнить ФЗ так, чтобы можно было использовать аксиомы.

Правило объединения

Если X → Y и X → Z, то X → YZ

Доказательство:

X → XY (1 ФЗ и пополняем X);
XY → YZ (2 ФЗ и пополняем Y);
X → YZ (по аксиоме транзитивности).

Правило декомпозиции

Если X → Y, а Z ⊆ Y, то X → Z

Доказательство:

X → Y (по условию);
Y → Z (по аксиоме рефлексивности);
X → Z (по аксиоме транзитивности).

Правило псевдотранзитивности

Если X → Y и WY → Z, то WX → Z

Доказательство:

WX → WY (1 ФЗ и пополняем W);
WY → Z (по условию);
WX → Z (по аксиоме транзитивности).

Замыкание множества атрибутов

Замыкание F + может включать в себя очень большое количество ФЗ. Например:

F =(X → A 1, X → A 2... X → An)

X → Y ⊆ F +

Y ⊆(A 1, A 2... An) и таких подмножеств может быть 2 n

Поэтому "в лоб" замыкание F + никто не строит. Но необходимо найти какой-то метод, который достаточно просто позволял бы выяснять, принадлежит ли произвольная ФЗ X → Y к F +

Для этого применяется замыкание множества атрибутов.

Пусть R - универсальная схема отношения, а X - некоторое подмножество атрибутов. Тогда замыканием множества атрибутов X + называется совокупность атрибутов Ai 1, Ai 2... Aik таких, что X → Ai 1, X → Ai 2... X → Aik

Алгоритм построения

Алгоритм является итерационной процедурой.

полагаем i =0 и X +0= X, а X + i - замыкание множества атрибутов на i-том шаге;
X + i +1= X + i ⋃ V, где V - такое множество атрибутов в F, что существует ФЗ Y → Z, где Y ⊆ X + i, V ⊆ Z;
если X + i +1= X + i, то X += X + i, иначе i = i +1 и возвращаемся в пункт 2.