| 1. Вероятностные распределения | ||
| № задания | Вопросы или задачи | Предлагаемые ответы |
| 1.1 | Распределение вероятностей непрерывной случайной величины, которое описывается плотностью
 , называется , называется
| 1) Эмпирическим 2) Нормальным (*) 3) Равномерным 4) Вероятным 5) Невероятным |
| 1.2 | Распределение относительных частот называется | 1) Показательным 2) Теоретическим 3) Эмпирическим (*) 4) Вероятным 5) Невероятным |
| 1.3 | Распределение вероятностей непрерывной случайной величины Х, которое описывается плотностью  , называется , называется
| 1) Равномерным 2) Нормальным 3) Неравномерным 4) Показательным (*) 5) Биномиальным |
| 1.4 | Распределение вероятностей непрерывной случайной величины Х, которое описывается плотностью. 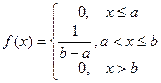 , называется , называется
| 1) Нормальным 2) Неравномерным 3) Показательным 4) Биномиальным 5) Равномерным (*) |
| 1.5 | Формула 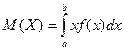 для непрерывной случайной величины выражает для непрерывной случайной величины выражает
| 1) Дисперсию 2) Среднее квадратическое отклонение 3) Генеральное среднее 4) Математическое ожидание (*) 5) Выборочное среднее |
| 1.6 | Формула  для непрерывной случайной величины выражает для непрерывной случайной величины выражает
| 1) Дисперсию (*) 2) Математическое ожидание 3) Вероятность 4) Частоту 5) Относительную частоту |
| 1.7 | Через моменты какого порядка находится асимметрия случайной величины? | 1) 3; 2) 1,2,4; 3) 1,2,3 (*) |
| 1.8 | Через моменты какого порядка находится эксцесс случайной величины? | 1) 3; 2) 1,2,4; (*) 3) 1,2,3 |
| 1.9 | Численная мера объективной возможности появления события в данном испытании называется | 1) Вероятностью (*) 2) Опытом 3) Исходом 4) Результатом 5) Событием |
| 1.10 | Сумма вероятностей противоположных событий равна | 1) 1 (*) 2) 0 3) 2 4) 0,5 5) -1 |
| 1.11 | Вероятность события В, вычисленную в предположении, что событие А уже наступило, называют | 1) Определенной 2) Несовместной 3) Условной (*) 4) Неопределенной 5) Равной |
| 2. Основные понятия математической статистики | ||
| № задания | Вопросы или задачи | Предлагаемые ответы |
| 2.1 | Отрасль знаний, объединяющая принципы и методы работы с числовыми данными, характеризующими массовые явлениями, называется | 1) Математикой 2) Экономикой 3) Эконометрикой 4) Статистикой 5) Макроэкономикой |
| 2.2 | Статистическая оценка, математическое ожидание которой равно оцениваемому параметру при любом объеме выборки, называется | 1) Вероятной 2) Несмещенной 3) Невероятной 4) Прямой 5) Обратной |
| 2.3 | Статистическая оценка, которая (при заданном объеме выборки) имеет наименьшую возможную дисперсию, называется | 1) Нормальной 2) Вероятной 3) Невероятной 4) Прямой 5) Эффективной |
| 2.4 | Статистическая оценка, которая при. 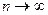 стремится по вероятности к оцениваемому параметру, называется стремится по вероятности к оцениваемому параметру, называется
| 1)Прямой 2) Вероятной 3) Невероятной 4) Состоятельной 5) Нормальной |
| 2.5 | Среднее арифметическое квадратов отклонений значений признака генеральной совокупности от их среднего значения, называется | 1) Генеральной дисперсией 2) Средней 3) Математическим ожиданием 4) Среднеквадратическим отклонением 5) Частотой |
| 2.6 | Дисперсию, взвешенную по объемам групп, называют | 1) Внутригрупповой 2) Генеральной 3) Средней 4) Взвешенной 5) Прямой |
| 2.7 | Можно ли использовать в качестве критерия согласия хи-квадрат критерий Пирсона? | 1) Да; 2) Нет; 3) Требует модификации |
| 2.8 | Проведено 5 измерений (без систематических ошибок) некоторой случайной величины: 6, 7, 8, 10, 11. Тогда несмещенная оценка математического ожидания равна… | 1) 8.2 2) 10.5 3) 8 4) 8.4 |
| 2.9 | В результате измерений некоторой физической величины одним прибором (без систематических ошибок) получены следующие результаты (в мм): 8, 11, 11. Тогда несмещенная оценка дисперсии измерений равна… | 1) 12 2) 9 3) 3 4) 6 |
| 2.10 | Точечная оценка параметра распределения равна 21. Тогда его интервальная оценка может иметь вид… | 1) [20 21]; 2) [21 22]; 3) [0 21]; 4) [20 22] |
| 2.11 | В результате измерений некоторой физической величины одним прибором (без систематических ошибок) получены следующие результаты (в мм): 8, 11, 11. Известно, что теоретическое среднее равно 10. Тогда несмещенная оценка дисперсии измерений равна… | 1) 12 2) 9 3) 2 4) 3 |
| 3. Основные характеристики законов распределения и их эмпирические аналоги | ||
| № задания | Вопросы или задачи | Предлагаемые ответы |
| 3.1 | Случайная величина x принимает значения 0, 1, 2, 3 с вероятностями, соответственно, 0.3, 0.4, 0.2, 0.1. Чему равно ее математическое ожидание? | 1) 0.15 2) 0.9 3) 0.11 (*) |
| 3.2 | Плотность распределения случайной величины X
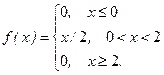 Чему равна ее медиана?
Чему равна ее медиана?
| 1) 1
2) 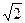 (*)
3) 3/4
4) 0.5
5) 1.5 (*)
3) 3/4
4) 0.5
5) 1.5
|
| 3.3 | Дана случайная выборка x 1,…, xn. Известно, что теоретическое распределение имеет конечные моменты до 4-го порядка. Теоретическое среднее известно и равно a. Как вычислить оценку теоретической дисперсии? | 1) 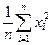 2)
2) 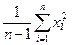 3)
3) 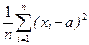 (*)
4) (*)
4) 
|
| 3.4 | Дана случайная выборка x 1,…, xn. Известно, что теоретическое распределение имеет конечные моменты до 4-го порядка. Как вычислить оценку теоретической дисперсии? | 1) 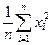 2)
2) 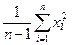 3)
3) 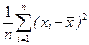 4)
4) 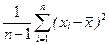 (*) (*)
|
| 3.5 | Одномерная случайная величина X распределена дискретно с рядом распределения xk -1 1 2 pk 0.2 0.5 0.3 Найти закон распределения случайной величины Y = X2 | 1. yk 2 3 5 qk 0.2 0.5 0.3 2. yk 1 4 qk 0.7 0.3 (*) 3. yk 1 3 qk 0.6 0.4 |
| 4. Системы случайных величин | ||
| № задания | Вопросы или задачи | Предлагаемые ответы |
| 4.1 | Дан случайный вектор  с вероятностной плотностью f (x, y). При выполнении какого условия его компоненты являются независимыми случайными величинами? с вероятностной плотностью f (x, y). При выполнении какого условия его компоненты являются независимыми случайными величинами?
| 1) f (x, y)= =fξ (x). fη (y); (*) 2) cov(ξη)=0; 3) corr(ξη)=0 |
| 4.2 | Дан случайный вектор  с вероятностной плотностью f (x, y). При выполнении какого условия его компоненты являются некоррелированными случайными величинами? с вероятностной плотностью f (x, y). При выполнении какого условия его компоненты являются некоррелированными случайными величинами?
| 1) cov(ξη)=0; (*) 2) f (x, y) симметрична по x и по y 3) M(ξη)= M(ξ) M(η) |
| 4.3 | Даны случайные величины ξ, η. При каком условии D(ξη)= D(ξ) +D(η)? | 1) f (x, y) симметрична по x и по y 2) cov(ξ,η)=0; (*) 3) M(ξη)= M(ξ) M(η) |
| 4.4 | Дан случайный вектор  . По какой формуле вычисляется его ковариационная матрица? . По какой формуле вычисляется его ковариационная матрица?
| 1) M[(ξ- M ξ)(η -M η)] 2) M[ ξη)] 3) M[(X -M X)(X -M X)T] (*) |
| 5. Многомерный нормальный закон | ||
| № задания | Вопросы или задачи | Предлагаемые ответы |
| 5.1 |  – гауссов случайный вектор с вероятностной плотностью z = f (x, y). Какое из следующих утверждений справедливо? – гауссов случайный вектор с вероятностной плотностью z = f (x, y). Какое из следующих утверждений справедливо?
| 1) ξ и η – гауссовы случайные величины; (*) 2) ξ и η – гауссовы, если cov(ξ,η)=0; 3) ξ и η – гауссовы, если M(ξη)= M(ξ) M(η) |
| 5.2 |  – гауссов случайный вектор с вероятностной плотностью z = f (x, y). Какой класс кривых получается при сечении поверхности z = f (x, y) плоскостями z = const? – гауссов случайный вектор с вероятностной плотностью z = f (x, y). Какой класс кривых получается при сечении поверхности z = f (x, y) плоскостями z = const?
| 1) Гиперболы; 2) Эллипсы; (*) 3) Параболы |
| 5.3 |  – гауссов случайный вектор, – гауссов случайный вектор, 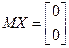 , ,  Ф(х) – функция Лапласа. Чему равна вероятность попадания Х в полосу Ф(х) – функция Лапласа. Чему равна вероятность попадания Х в полосу 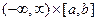 ? ?
| 1) Ф(b)-Ф(a) 2) [Ф(b)-Ф(a)]/2 3) Ф(b /2)-Ф(a /2) (*) |
| 5.4 |  – гауссов случайный вектор, – гауссов случайный вектор,  Какая из осей эллипса рассеяния больше? Какая из осей эллипса рассеяния больше?
| 1) Та, которая параллельна оси Ox; 2) Та, которая параллельна оси Oy; 3) Оси равны |
| 5.5 | Как называется параметр “n” в распределении Пирсона

| 1. Математическое ожидание 2. Число степеней свободы (*) 3. Дисперсия |
| 6. Функции от случайных величин | ||
| № задания | Вопросы или задачи | Предлагаемые ответы |
| 6.1 | Дана случайная величина ξ с вероятностной плотностью f (x). Чему равно математическое ожидание величины ξ 2? | 1)  (*)
2) (*)
2)  3)
3) 
|
| 6.2 | Дана случайная величина ξ с функцией распределения F (x). Чему равна функция распределения величины 2 ξ? | 1) F (2 x) 2) F (x /2) (*) 3) F (x)- F (- x) |
| 6.3 | Дана непрерывная случайная величина ξ с функцией распределения F (x). Чему равна функция распределения величины 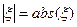 ? ?
| 1) F (2 x) 2) F (x /2) 3) F (x)- F (- x) (*) |
| 6.4 |  – случайный вектор, – случайный вектор,  Чему равна дисперсия величины 2 ξ + η? Чему равна дисперсия величины 2 ξ + η?
| 1) 8; 2) 12; 3) 4; 4) 2 (*) |
| 7. Основные распределения, связанные с нормальным законом | ||
| № задания | Вопросы или задачи | Предлагаемые ответы |
| 7.1 | Даны независимые одинаково распределенные случайные величины x 1,…, xn с известными общими математическим ожиданием a и дисперсией σ2.
 Какому закону подчиняется случайная величина
Какому закону подчиняется случайная величина
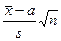 ? ?
| 1) N (0,1) 2) Стьюдента с n степенями свободы (*) 3) Стьюдента с (n -1) степенью свободы 4) Хи-квадрат с n степенями свободы 5) Хи-квадрат с (n -1) степенью свободы |
| 7.2 | Даны независимые одинаково распределенные случайные величины x 1,…, xn с известными общими математическим ожиданием a и дисперсией σ2.
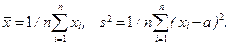 Какому закону подчиняется случайная величина
Какому закону подчиняется случайная величина
 ? ?
| 1) N (0,1) (*) 2) Стьюдента с n степенями свободы 3) Стьюдента с (n -1) степенью свободы 4) Хи-квадрат с n степенями свободы 5) Хи-квадрат с (n -1) степенью свободы |
| 7.3 | Даны независимые одинаково распределенные случайные величины x 1,…, xn с известными общими математическим ожиданием a и дисперсией σ2.
 Какому закону подчиняется случайная величина
Какому закону подчиняется случайная величина
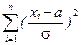 ? ?
| 1) Стьюдента с n степенями свободы 2) Стьюдента с (n -1) степенью свободы 3) Хи-квадрат с n степенями свободы (*) 4) Хи-квадрат с (n -1) степенью свободы |
| 7.4 | Даны независимые одинаково распределенные случайные величины x 1,…, xn с известными общими математическим ожиданием a и дисперсией σ2.
 Какому закону подчиняется случайная величина
Какому закону подчиняется случайная величина
 ? ?
| 1) Стьюдента с n степенями свободы 2) Стьюдента с (n -1) степенью свободы 3) Хи-квадрат с n степенями свободы 4) Хи-квадрат с (n -1) степенью свободы (*) |
| 8. Основные понятия математической статистики. Основные задачи | ||
| № задания | Вопросы или задачи | Предлагаемые ответы |
| 8.1 | Выборка x 1,…, xn представлена в виде вариационного ряда x( 1),…, x(n). Как определяется x( 1)? | 1) x( 1)=min{ x(i )} (*) 2) x( 1)=max{ x(i )} 3) x( 1)=(x 1+ xn)/2 |
| 8.2 | Выборка x 1,…, x 21 представлена в виде вариационного ряда x( 1),…, x(21). Как найти оценку  медианы m генеральной совокупности? медианы m генеральной совокупности?
| 1)  = x (11) (*)
2) = x (11) (*)
2)  =(x (10)+ x (11))/2
3) =(x (10)+ x (11))/2
3)  =(x (1)+ x (21))/2 =(x (1)+ x (21))/2
|
| 8.3 | По выборке x 1,…, xn с теоретической плотностью f (x) вычислены статистики
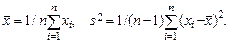 При каком условии s 2 является состоятельной оценкой теоретической дисперсии?
При каком условии s 2 является состоятельной оценкой теоретической дисперсии?
| 1) Всегда
2) Если f (x) симметрична
3) Если  (*)
(*)
|
| 8.4 | Выборочные значения x 1,…, xn – н.о.р.  В каком случае статистика В каком случае статистика  является несмещенной оценкой параметра является несмещенной оценкой параметра  ? ?
| 1) Если 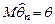 (*)
2) Если (*)
2) Если 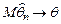 при при 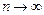 3) Если
3) Если 
|
| 8.5 | Выборочные значения x 1,…, xn – н.о.р.  Имеются две асимптотически несмещенные оценки параметра Имеются две асимптотически несмещенные оценки параметра  , ,  и и 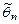 . Как вычисляется асимптотическая эффективность . Как вычисляется асимптотическая эффективность  по отношению к по отношению к 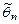 ? ?
| 1) 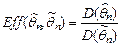 2) (*)
2) (*)  3)
3) 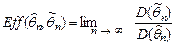
|
| 9. Оценивание центра симметричного распределения: асимптотическая нормальность, неравенство Рао-Крамера, метод максимального правдоподобия | ||
| № задания | Вопросы или задачи | Предлагаемые ответы |
| 9.1 | Выборочные значения x 1,…, xn – н.о.р.  , f (x) симметрична. Имеется подозрение на наличие в выборке нескольких грубых ошибок. Какую оценку параметра , f (x) симметрична. Имеется подозрение на наличие в выборке нескольких грубых ошибок. Какую оценку параметра  следует предпочесть? следует предпочесть?
| 1) Выборочное среднее
2) Выборочную медиану (*)
3) Середину размаха

|
| 9.2 | Что устанавливает неравенство Рао-Крамера? | 1) Нижнюю границу асимптотической дисперсии оценки 2) Верхнюю границу асимптотической дисперсии оценки (*) 3) Верхнюю границу асимптотического смещения оценки |
| 9.3 | x 1,…, xn – выборка из равномерного распределения U ( - l, - l,  + l). Какая из оценок параметра + l). Какая из оценок параметра  имеет наибольшую эффективность и является оценкой максимального правдоподобия? имеет наибольшую эффективность и является оценкой максимального правдоподобия?
| 1) Выборочное среднее
2) Выборочная медиана
3) Середина размаха
 (*) (*)
|
| 9.4 | x 1,…, xn – выборка из равномерного распределения U ( - l, - l,  + l). Какая из приведенных оценок теоретической дисперсии имеет наибольшую эффективность и является оценкой максимального правдоподобия? + l). Какая из приведенных оценок теоретической дисперсии имеет наибольшую эффективность и является оценкой максимального правдоподобия?
| 1) Выборочная дисперсия s 2
2) Медианный размах med{ xi -med(xi)}
3) Выборочный размах
 (*) (*)
|
| 9.5 | x 1,…, xn – выборка из нормального распределения N ( ,s2). Какая из оценок параметра ,s2). Какая из оценок параметра  имеет наибольшую эффективность и является оценкой максимального правдоподобия? имеет наибольшую эффективность и является оценкой максимального правдоподобия?
| 1) Выборочное среднее (*)
2) Выборочная медиана
3) Середина размаха

|
| 10. Принципы проверки гипотез | ||
| № задания | Вопросы или задачи | Предлагаемые ответы |
| 10.1 | На основе выборки x 1,…, xn – н.о.р. 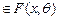 проверяется гипотеза H 0: проверяется гипотеза H 0:  = =  0 против альтернативы H 1: 0 против альтернативы H 1:  = =  1. Что контролирует ошибку первого рода? 1. Что контролирует ошибку первого рода?
| 1) Выбор статистики критерия 2) Выбор границы критической зоны (*) |
| 10.2 | На основе выборки x 1,…, xn – н.о.р. 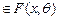 проверяется гипотеза H 0: проверяется гипотеза H 0:  = =  0 против альтернативы H 1: 0 против альтернативы H 1:  = =  1. Что контролирует ошибку второго рода? 1. Что контролирует ошибку второго рода?
| 1) Выбор статистики критерия (*) 2) Выбор границы критической зоны |
| 10.3 | a - вероятность ошибки 1-го рода (вероятность пропуска цели), b - вероятность ошибки 2-го рода (вероятность ложной тревоги). Как определяется уровень значимости критерия? | 1) 1- a (*) 2) 1- b |
| 10.4 | a - вероятность ошибки 1-го рода (вероятность пропуска цели), b - вероятность ошибки 2-го рода (вероятность ложной тревоги). Как определяется мощность критерия? | 1) 1- a 2) 1- b (*) |
| 11. Основные критерии нормальной теории | ||
| № задания | Вопросы или задачи | Предлагаемые ответы |
| 11.1 | На основе выборки x 1,…, xn – н.о.р.  при неизвестной дисперсии проверяется гипотеза H 0: a = a 0 против альтернативы H 1: a = a 1. Какую статистику T следует использовать в решающем правиле для достижения наибольшей мощности? при неизвестной дисперсии проверяется гипотеза H 0: a = a 0 против альтернативы H 1: a = a 1. Какую статистику T следует использовать в решающем правиле для достижения наибольшей мощности?
| 1) 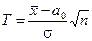 2)
2)  (*)
3) (*)
3) 
|
| 11.2 | На основе выборки x 1,…, xn – н.о.р.  при известной дисперсии проверяется гипотеза H 0: a = a 0 против альтернативы H 1: a = a 1. Решающее правило основано на статистике при известной дисперсии проверяется гипотеза H 0: a = a 0 против альтернативы H 1: a = a 1. Решающее правило основано на статистике 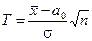 . Какому закону распределения подчиняется эта статистика при условии справедливости H 0? . Какому закону распределения подчиняется эта статистика при условии справедливости H 0?
| 1) Нормальному N (0,1) 2) Распределению Стьюдента с n степенями свободы 3) Распределению Стьюдента с n -1 степенью свободы 4) Распределению хи-квадратс n степенями свободы 5) Распределению хи-квадрат с n -1 степенью свободы. |
| 11.3 | На основе выборки x 1,…, xn – н.о.р. 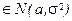 при неизвестном a проверяется гипотеза H 0: σ=σ 0 против альтернативы H 1: σ = σ 1. Решающее правило основано на статистике при неизвестном a проверяется гипотеза H 0: σ=σ 0 против альтернативы H 1: σ = σ 1. Решающее правило основано на статистике  . Какому закону распределения подчиняется эта статистика при условии справедливости H 0? . Какому закону распределения подчиняется эта статистика при условии справедливости H 0?
| 1) Нормальному N (0,1) 2) Распределению Стьюдента с n степенями свободы 3) Распределению Стьюдента с n -1 степенью свободы 4) Распределению хи-квад- рат с n степенями свободы 5) Распределению хи-квадрат с n -1 степенью свободы (*) |
| 12. Линейная модель измерений | ||
| № задания | Вопросы или задачи | Предлагаемые ответы |
| 12.1 | Набор экспериментальных точек (xi, yi), i =1,…, n аппроксимируется полиномом 1-й степени с вектором коэффициентов a =(a 0, a 1) на основе МНК. Как устроена матрица Х соответствующей линейной модели? | 1)  (*)
2) (*)
2)  3)
3)  4) Модель не является линейной
4) Модель не является линейной
|
| 12.2 | Измерения имеют вид yi = axi +ξi, i =1,…, n, ξi -н.о.р., коэффициенты xi известны. Ищется МНК-оценка параметра наклона a. Как устроена матрица Х соответствующей линейной модели? | 1)  2)
2)  (*)
3) Модель не является линейной (*)
3) Модель не является линейной
|
| 12.3 | Для экспериментальные точек (xi, yi), i =1,…, n строится интерполяционный полином Лагранжа, а затем этот набор точек аппроксимируется по МНК полиномом степени (n -1). Совпадут или нет коэффициенты этих полиномов? | 1) Совпадут (*) 2) Не совпадут |
| 13. Оценка по МНК и ее свойства | ||
| № задания | Вопросы или задачи | Предлагаемые ответы |
| 13.1 | Измерения имеют вид yi = axi +ξi, i =1,…, n, ξi -н.о.р. 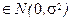 , коэффициенты xi известны. Ищется МНК-оценка параметра наклона a. Будет ли эта оценка несмещенной? , коэффициенты xi известны. Ищется МНК-оценка параметра наклона a. Будет ли эта оценка несмещенной?
| 1) Оценка несмещенная (*) 2) Оценка является асимптотически-несмещенной 3) Оценка может иметь смещение, зависящее от { xi } |
| 13.2 | Измерения имеют вид yi = axi +ξi, i =1,…, n, ξi -н.о.р. 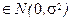 , коэффициенты xi известны и различны. Ищется МНК-оценка параметра наклона a. Как соотносится дисперсия этой оценки с границей, даваемой неравенством Рао-Крамера? , коэффициенты xi известны и различны. Ищется МНК-оценка параметра наклона a. Как соотносится дисперсия этой оценки с границей, даваемой неравенством Рао-Крамера?
| 1) Дисперсия оценки ниже границы Рао-Крамера 2) Дисперсия оценки совпадает с границей Рао-Крамера (*) 1) Дисперсия оценки выше границы Рао-Крамера |
| 13.3 | Модель измерений имеет вид Y = X θ+ξ, матрица X имеет размер  , ξ i – н.о.р. гауссовы погрешности с нулевым средним и дисперсией σ2. Какому закону подчиняется оценка вектора θ? , ξ i – н.о.р. гауссовы погрешности с нулевым средним и дисперсией σ2. Какому закону подчиняется оценка вектора θ?
| 1) N (0, σ2) 2) Nk (0, σ2) 3) Nk (θ, σ2(ATA)) 4) Nk (θ, σ2(ATA)-1) |
| 13.4 | Для экспериментальные точек (xi, yi), i =1,…, n строится интерполяционный полином Лагранжа, а затем этот набор точек аппроксимируется по МНК полиномом степени (n -3). Совпадут или нет коэффициенты этих полиномов? | 1) Совпадут 2) Не совпадут (*) |
| 13.5 | Измерения имеют вид yi = axi +ξi, i =1,…, n, ξi -н.о.р., коэффициенты xi известны. Ищется МНК-оценка параметра наклона a. Найти дисперсию оценки. | 1)  2)
2)  (*)
3) (*)
3) 
|
| 14. Вычислительные трудности МНК | ||
| № задания | Вопросы или задачи | Предлагаемые ответы |
| 14.1 | Модель измерений имеет вид Y = X θ+ξ, матрица X имеет размер 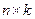 , ξ i – н.о.р. гауссовы погрешности с нулевым средним и дисперсией σ2. Минимальное собственное число матрицы XTX оказалось близким к нулю. Можно ли повысить точность, не изменяя структуру модели? , ξ i – н.о.р. гауссовы погрешности с нулевым средним и дисперсией σ2. Минимальное собственное число матрицы XTX оказалось близким к нулю. Можно ли повысить точность, не изменяя структуру модели?
| 1) Точность повысить нельзя 2) Можно уменьшить полный квадрат ошибки, введя в оценку смещение |
| 14.2 | Набор экспериментальных точек (xi, yi), i =1,…, n аппроксимируется полиномом k -й степени в линейной модели с матрицей регрессионных коэффициентов X. Минимальное собственное число матрицы XTX оказалось равным нулю. Как следует видоизменить модель? | 1) Уменьшить степень k (*) 2) Увеличить степень k 3) Данные противоречивы |
| 14.3 | Модель измерений имеет вид Y = X θ+ξ, матрица X имеет размер 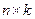 , ξ i – н.о.р. гауссовы погрешности с нулевым средним и дисперсией σ2. Рассматриваются оценка по МНК , ξ i – н.о.р. гауссовы погрешности с нулевым средним и дисперсией σ2. Рассматриваются оценка по МНК  и оценка хребтовой регрессии и оценка хребтовой регрессии 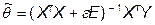 . Как соотносятся свойства этих оценок? . Как соотносятся свойства этих оценок?
| 1) В общем случае неизвестно 2) Оценка по МНК всегда более эффективна 3) Оценка хребтовой регрессии имеет смещение, но дисперсии ее компонент меньше. (*) |
 2020-10-10
2020-10-10 550
550






