З акон сохранения импульса: Импульс замкнутой механической системы сохраняется, т.е. не изменяется с течением времени.

Импульс (геометрическая сумма импульсов взаимодействующих тел) системы до взаимодействия равен импульсу системы после взаимодействия.
Пример для двух взаимодействующих тел…
Следует отметить, что импульс остаётся постоянным и для незамкнутой системы при условии, что сумма внешних сил в сумме равна нулю.
Этот закон является фундаментальным законом природы и справедлив не только в рамках классической механики.
2.1. МОМЕНТ ИНЕРЦИИ ОТНОСИТЕЛЬНО ОСИ ВРАЩЕНИЯ.
 |

Если тело вращается вокруг неподвижной оси, линейная скорость i -той точки может быть определена:

Следовательно, кинетическая энергия i -той точки, имеющей массу mi равна
 =
= 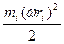
 - т.к. все точки тела имеют одинаковую угловую скорость.
- т.к. все точки тела имеют одинаковую угловую скорость.
Учитывая, что любое тело можно разбить на элементарные массы mi и рассматривать его как систему материальных точек, взаимное расположение которых не меняется, кинетическая энергия тела в целом будет складываться из кинетической энергии его частей.
 , (т.к.
, (т.к.  const)
const) 
Введем обозначение  - произведение массы точки на квадрат расстояния её до оси вращения называется моментом инерции точки относительно неподвижной оси вращения.
- произведение массы точки на квадрат расстояния её до оси вращения называется моментом инерции точки относительно неподвижной оси вращения.
 - сумма моментов инерции отдельных точек тела равна моменту инерции тела в целом относительно неподвижной оси (кг.м2).
- сумма моментов инерции отдельных точек тела равна моменту инерции тела в целом относительно неподвижной оси (кг.м2).
Т.о. величина, учитывающая массу вращающегося тела и распределение её относительно оси вращения называется моментом инерции тела относительно заданной оси вращения.
Для данного тела момент инерции (J = const) величина постоянная. При m = const J тем больше, чем дальше материальные точки тела отстоят от оси вращения.
| |
 (1), т. к.
(1), т. к. 
Полученное выражение аналогично выражению кинетической энергии движущегося поступательно тела.
 (2)
(2)
Из сравнения (1) и (2) видно, что при вращательном движении роль массы играет момент инерции, а роль линейной скорости – угловая скорость.
 ω υ
ω υ
 J m
J m
Если тело участвует одновременно в двух движениях поступательном и вращательном, то его кинетическая энергия складывается из кинетической энергии поступательного и кинетической энергии вращательного движения.

Теорема Штейнера (теорема о переносе осей).
Момент инерции J тела относительно произвольной оси равен сумме моментов инерции этого тела Jc относительно оси, проходящей через центр инерции тела (центр масс) параллельно рассматриваемой оси и произведения массы тела m на квадрат расстояния d между осями.
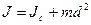

 2020-10-11
2020-10-11 196
196








