Логистическая модель роста

Описывается S-образной кривой. В реальных условиях численность популяции после начального периода экспоненциального роста выходит на плато - стационарный режим.

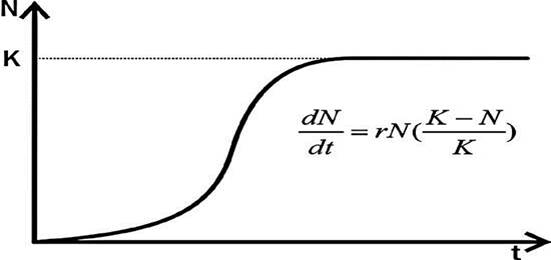
В основе логистической модели лежит простое допущение, что мгновенная удельная скорость роста r = линейно снижается по мере увеличения численности N.

Для описания S-образной кривой предложено достаточно большое количество уравнений. Но наибольшую известность в экологии приобрело логистическое уравнение.

Его предложил Ферхюльст в 1838 г. Для описания динамики народонаселения.

А в 1920 уравнение переоткрыли независимо друг от друга Пирл и Рид. В итоге уравнение Ферлюхста, Пирла - Рида.

В основе логистической модели лежит простое предположение, что мгновенная удельная скорость роста [r (а) = ] линейно снижается по мере увеличения численности N.

То есть r(a) ≠ const, как в экспоненциальной модели! То есть, если численность реальной популяции ограничивается величиной К (тем-ра, пища, свет и т.д.), то r = 0 в том случае, когда численность достигла уровня Nk [N=Nk]. То есть численность достигла своего максимального размера при данном ограничивающем факторе.

Nk еще называют биологической емкостью среды – это степень способности природного или природно-антропогенного окружения обеспечивать нормальную жизнедеятельность определенному числу организмов и их сообществ без заметного нарушения самого окружения.

АВ – линейный отрезок, описываемый уравнением типа y=b-ax

y – изменение мгновенной удельной скорости

b – r в точке А

ах - r· → так как если N достигнет Nk, то = 1

r-1 ·r = 0 = точка В.

Таким образом составные части уравнения работают

Записываем уравнение полностью

V роста = · =r – r

= r (1 - - ):

= r_max N () – уравнение Ферхюльста -Пирли -Рида.

Nt =

r_max= r_эксп

Несмотря на то, что r принимает разные значения (constanta или не constanta), r сохраняет свой смысл r = b- d.

Если r изменится с изменением численности, то и b и d (смертность и рождаемость) также изменятся с изменением численности.

N₀ – рождаемость > смертности (начальная численность популяции)

N растет и помним, что r падает. Тогда по логике рождаемость снижается, а смертность увеличивается.

Z – точка, где b = d – стационарный уровень соответствует максимальной численности популяции Nk.

Если наложить на график экспоненциального роста логистическую кривую, то получится пространство между J-образной кривой (рост в отсутствии лимитирующих факторов) и S-образной кривой (рост в условиях ограничений). Это пространство называют сопротивлением среды. Чем меньше сопротивление среды, тем ближе S-образная кривая к J-образной кривой.

Логистическая модель, имея в основе линейное снижение удельной скорости роста по мере возрастания численности (плотности) популяции, однако же не основана и не вытекает из особенностей самих организмов. Хотя мы можем представить черты популяции, изменение численности которой описывается S-образной кривой.

1. Все особи одинаковые → потребность одинаковая, количество ресурса, они должны быть в одинаковых условиях относительно смертности и рождаемости.

2. Реакция на увеличение численности популяции (увеличение плотности) со стороны особей должна быть мгновенной и провялятся в снижении рождаемости и увеличении смертности.

На самом деле мы наблюдаем запаздывание – лаг-эффект, что можно учесть (пример)

= r_maxNt ()

Nt -τ – численность наблюдавшаяся за время τ до момента t

Теоретическое исследование логистической модели с запаздыванием показало, что ей свойственен колебательный режим, причем при увеличении времени запаздывания и величины r_max возрастает амплитуда и частота таких колебаний.

Логистический рост

Задача

= r N (1 - )

N(t) =

Емкость среды 5000 клеток. Начальная численность – 10 клеток, через 20 минут 40 клеток. Постройте график логистического роста.

В начальный период действие лимитирующих факторов сведено к min → рост можно приравнять к росту в идеальных условиях

Nt = N₀ e^rt

Найдем из этого уравнения r- специфическую скорость роста

40 = 10 ·e^20·r

4 = e^20r

ln 4 = 20 r

r = = 0,07

Будем следить за изменением численности популяции через равные промежутки времени - 20 минут, при этом N₀ – предыдущая численность популяции будет иметь всегда свои значения.

N₄₀ = = 158