Уравнения, решение которых основано на свойствах модуля

Уравнения, содержащие неизвестное под знаком модуля

Уравнения вида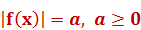

Наиболее рациональный путь решения – переход к совокупности .

Уравнения вида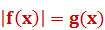

Такие уравнения можно двумя способами заменить равносильными условиям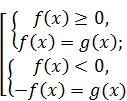и:  и .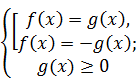

Выбор способа замены зависит от того, какое и неравенств 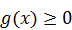 или  решить легче.

Пример 1. Решить уравнение .

Решение. Исходное уравнение равносильно совокупности 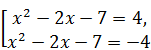 Û .

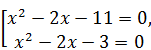Решая эти уравнения, получим корни х = ‑ 1; х =3; х =1±2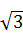

Ответ: ‑ 1; 3; 1±2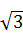

Пример 2. Решить уравнение .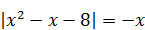

Решение. Исходное уравнение равносильно системе 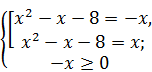 Û .

Решая эти уравнения, получим корни х = ‑ 2; х =4; х =±2 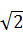. Но условию  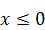удовлетворяют только числа – 2 и ‑ 2 .

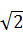Ответ: ‑ 2; ‑ 2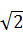

Пример 3. Решите уравнение .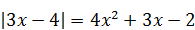

Решение. Поскольку в уравнении функция, стоящая под знаком модуля, проще, то лучше записать уравнение как совокупность двух систем:

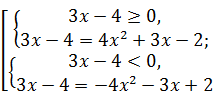 Û .

Уравнение из первой системы совокупности корней не имеет. Решением второй системы является .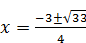

Ответ: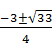

Уравнения вида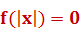

Уравнения этого вида можно решать, используя замену .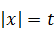

Пример 4. Решить уравнение .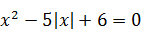

Решение. Так как 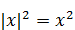, данное уравнение примет вид: .

Сделаем замену , получим новое уравнение 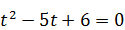, которое имеет два положительных корня t =2; t =3. Значит, | x |=2: | x |=3, откуда x =±2, x =±3.

Ответ: ‑ 2; 2; ‑ 3; 3

Пример 5. Решить уравнение .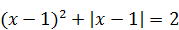

Решение. Так как , данное уравнение примет вид: . Сделаем замену 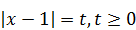, получим новое уравнение ; t = ‑ 2; t =1. Однако t = ‑ 2 не удовлетворяет условию .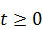

Получим уравнение 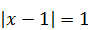. Откуда  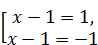Û .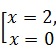

Ответ: 0; 2

Уравнения, решение которых основано на свойствах модуля

Пример 6. Решить уравнение .

Решение. Возведем обе части уравнения в квадрат:  Û .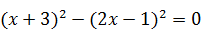

Используя формулу разности квадратов, разложим левую часть на множители: 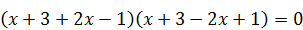 Û 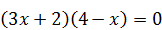. Откуда х = 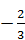; х =4.

Ответ: 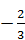; 4

Уравнения вида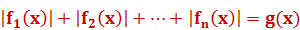

При решении таких уравнений применяется метод интервалов:

1. определяются точки, в которых каждая из функций равна нулю;

2. найденные промежутки разбивают область определения уравнения на промежутки, на каждом из которых все функции сохраняют знак;

3. исходное уравнение решается на каждом промежутке, при этом модули опускаются с учетом знака функций на рассматриваемом промежутке;

4. объединяются решения, найденные на всех частях области определения уравнения.

Пример 7. Решите уравнение .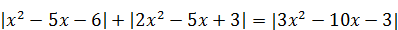

Решение. Заметим, что данное уравнение имеет вид .

Из свойств абсолютной величины следует, что это равенство справедливо тогда и только тогда, когда ab ³0. Поэтому исходное уравнение равносильно неравенству .

Корни трехчленов: x =6; x = ‑ 1; x = ; x =1. Решим неравенство методом интервалов:

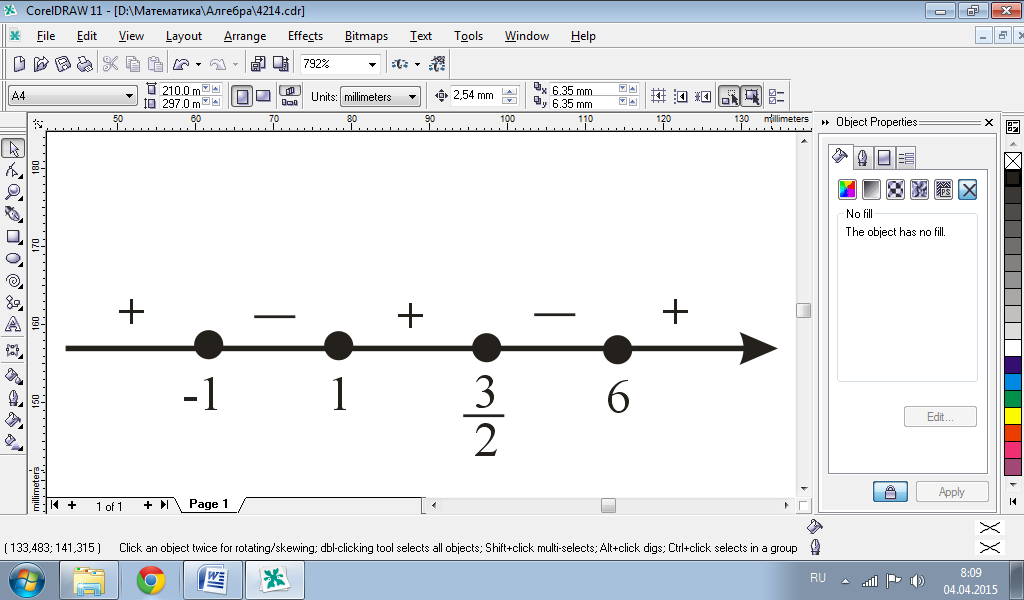
Ответ: (‑ ∞; ‑ 1]È[1; ]È[6; +∞)

Рассмотрим уравнение: |2 ‑ x |=16 – 2|5 – x | ‑ | x |

Шаг 1. Под каждым из модулей все слагаемые расположить в порядке убывания степеней х, причем коэффициент при старшей степени х сделать положительным числом.

|2 ‑ x |=16 – 2|5 – x | ‑ | x | Û | x – 2|+| x |+2| x – 5|=16.

Шаг 2. Определить нули каждого выражения под знаком модуля, присутствующего в уравнении (неравенстве). Эти точки разбивают область определения каждого подмодульного выражения на интервала знакопостонства.

Шаг 3. Нанести нули каждого из выражений на отдельную силовую прямую и расположить все эти прямые друг под другом. Указать на прямых такие промежутки, в пределах которых все подмодульные выражения одновременно сохраняют знакопостоянство.

Для нашего примера

Здесь на промежутках (‑ ∞; 0], (0; 2], (2; 5], (5; +∞) все подмодульные выражения одновременно являются знакопостоянными.

Шаг 4. На каждом из полученных промежутков раскрыть модули в соответствии со знаками подмодульных выражений на этом промежутке и решить соответствующее промежутку уравнение (неравенство). Все полученные решения объединить в общий ответ.

В нашем примере:

1)

2) .

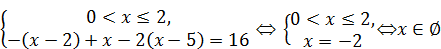3)

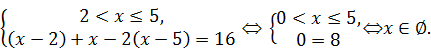
4)

Ответ: (‑ 1; 7)

Метод интервалов выручает в следующих ситуациях:

· Под знаком модуля встречаются не только линейные функции, но квадратичные, кубические, показательные и пр.;

· Формулировка задачи не обязательно сводится к решению уравнения или неравенства.