2020-10-11
79
симплекс-методом
Решить задачу ЛП двойственным симплекс-методом.
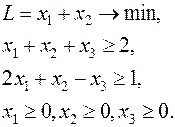
Приводим задачу к каноническому виду:
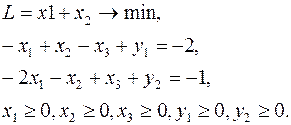
Знаки в ограничениях заменили противоположными для того, чтобы переменные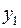 
и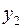 
можно было взять в качестве базисных. Симплексная таблица имеет вид
| b |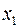 
| 
| 
| |
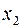
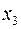
| L | 0 | -1 | -1 | 0 |
|
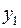
| -2 | -1 | 1 | -1 |
|
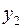
| -1 | -2 | -1 | 1 |
Таблица двойственно-допустимая, но не оптимальная. Выбираем ведущую строку – это строка переменной 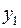, ведущий столбец – это столбец переменной 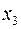. После преобразования таблица принимает вид
| b |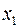
|
| 
| |
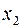
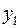
| L | 0 | -1 | -1 | 0 |
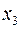
| 2 | 1 | -1 | -1 |
|
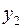
| -3 | -3 | 0 | 1 |
Так как в столбце b есть отрицательная переменная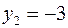 
, то эту строку выбираем ведущей, а столбец переменной 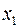будет ведущим столбцом. После преобразования получаем таблицу:
| b |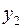
|
|
| |
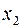
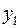
| L | 1 | -1/3 | -1 | -1/3 |
|
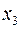
| 1 | 1/3 | -1 | -2/3 |
|
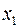
| 1 | -1/3 | 0 | -1/3 |
которая является оптимальной. Соответствующее оптимальное решение имеет вид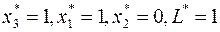 
.
Пример построения двойственной задачи
Построить двойственную задачу к следующей задаче ЛП.
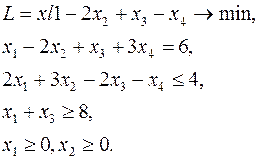
Прежде чем приступать к построению двойственной задачи, необходимо упорядочить запись исходной: согласовать знаки неравенств в ограничениях с целевой функцией. Так как ЦФ минимизируется, то неравенства должны быть записаны с помощью знака «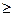
». Для этого второе неравенство умножим на -1:
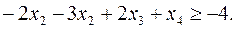
Теперь, вводя двойственные переменные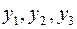 
, запишем в соответствии с указанным правилом пару двойственных задач:
| 
| |
| 
| |
| 
| |
| 
| |
| 
| |
| 
| |
| 
| |
| 
|
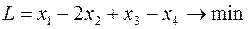
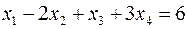
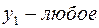
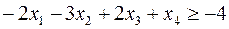
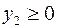
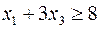
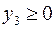
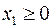
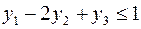
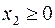
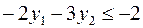
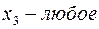
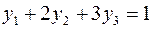
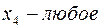
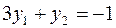
Задача слева – исходная прямая задача, задача справа – двойственная к исходной задаче.
