2020-10-11
82
Используя теоремы двойственности, решить двойственную задачу, если известно решение прямой задачи.
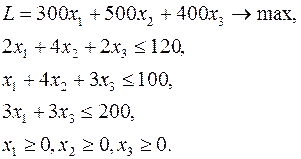(12)
Пусть решение задачи найдено одним из стандартных методов: 
. Построим двойственную задачу:
(13)
По первой теореме двойственности задача разрешима, причем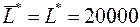 
. Найдем оптимальный план 
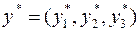задачи (13), используя вторую теорему двойственности. Подставим координаты вектора 
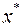в ограничения задачи (12). Получим
Следовательно, в силу УДН, неравенство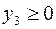 
должно выполняться как равенство, т. е. 
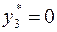. Далее так как 
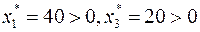, то в силу УДН,
.
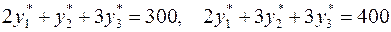Получаем систему линейных уравнений и решаем ее:
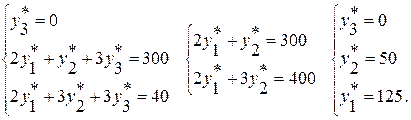
Планы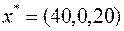 
и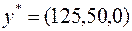 
удовлетворяют УДН, следовательно, в силу второй теоремы двойственности, являются оптимальными в задачах (12) и (13) соответственно.
Пример проверки вектора на оптимальность
Исследовать вектор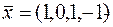 
на оптимальность в задаче ЛП.
Вначале нужно проверить, является ли вектор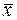 
допустимым. Для этого подставляем координаты вектора в ограничения:
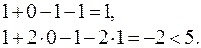
Так как второе ограничение выполняется как строгое неравенство, то в силу УДН для оптимальности вектора 
необходимо выполнение равенства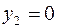 
.
Построим двойственную задачу:
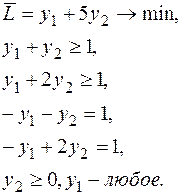
Поскольку 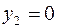, то из третьего и четвертого ограничений получаем 
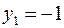. Но по УДН из условия 
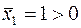следует, что должно выполняться равенство в первом ограничении двойственной задачи:
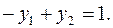
Подставляя значения 
получим 
Следовательно, УДН не выполняются и вектор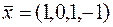 
не является оптимальным в исходной задаче.
