Підбір складеного перерізу суцільної колони

         За формулою обчислюємо стискаючу силу:

, де

n = 2- кількість головних балок, які спираються на середню колону;

 - опорна реакція головної балки.

Геометричну довжину колони обчислюємо за формулою:

Розрахункові довжини колони відносно головних осей її перерізу визначаємо за формулою:

.

За [1, табл.50*] для колони приймаємо сталь С235 з ; .

Задаємось орієнтовно гнучкістю колони  в межах 60..100; приймемо, наприклад, 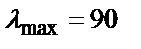 та знайдемо коефіцієнт поздовжнього згину . Із формули маємо необхідну площу перерізу колони:

.

Необхідний радіус інерції із формули:

Радіус інерції двотаврового перерізу:

.                                                 

Звідси знаходимо потрібну ширину полиці:

 .

Із умови загальної стійкості колони необхідно, щоб:

тобто

Використовуючи стандартні розміри широкополосної сталі, остаточно приймаємо

Граничне значення відношення звісу полиці до її товщини обчислюємо за формулою:

,

де умовна гнучкість

Якщо величина звісу полиці

,

то необхідна товщина полиці із умови її місцевої стійкості буде становити:           

.

Звичайно товщину полиці приймають не менш 10мм. =1

На практицізварнідвотавримаютьперерізи з розмірами , що є оптимальним для центрально-стиснутих колон. Ураховуючице, приймаємо

.

 Для забезпечення стійкості колони достатньо лише площі поясів, розміри стінки призначаємо конструктивно.

Висоту стінки маємо:

.

Товщину  необхідно визначити з умови місцевої стійкості стінки. При  за формулою знаходимо граничне значення :

 ,

Звичайно товщину стінки менше 6 мм не приймають, тому приймаємо .

Обчислюємо геометричні характеристики прийнятого перерізу:

площа перерізу

;

моменти інерції  

,

    ;

радіуси інерції     

   

Гнучкості за формулою:

За розрахункову беремо  .

Відповідна умовна гнучкість

Перевіряємо місцеву стійкість полиць за формулою:

У нас фактичний звіс полиць

,

і

- місцева стійкість полиць забезпечена.

Перевіряємо місцеву стійкість стінки за формулою.

Граничне співвідношення із:

Оскільки фактично маємо , місцева стійкість стінки забезпечена.

Перевіряємо загальну стійкість колони за формулою, для чого   визначаємо  і використовуємо формулу:

.