Обчислюємо умовну гнучкість стінки за формулою:
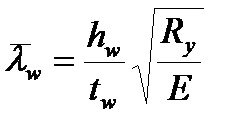 =
= 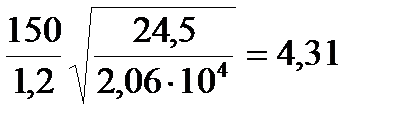 ;
;
звідси бачимо, що стінку балки необхідно підкріпити основними поперечними ребрами жорсткості з максимальним кроком
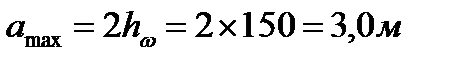 . При цьому, поздовжні ребра жорсткості не потрібні, бо
. При цьому, поздовжні ребра жорсткості не потрібні, бо 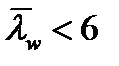 .
.
Мал. визначення місцевої стійкості стінки
З конструктивних міркувань крок поперечних ребер жорсткості вздовж стінки приймаємо 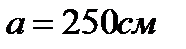 , тобто розміщуємо їх не під кожною балкою настилу, а через одну.
, тобто розміщуємо їх не під кожною балкою настилу, а через одну.
Ширина кожного з парних симетрично розташованих поперечних ребер жорсткості:
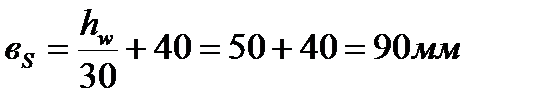 .
.
При цьому, товщина ребер повинна бути:
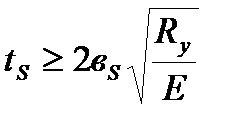 .
. 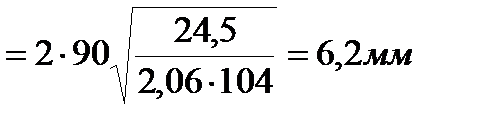
Місцеві напруження в стінці від опорної реакції балки настилу, що не має під собою поперечних ребер, обчислюємо за формулою:
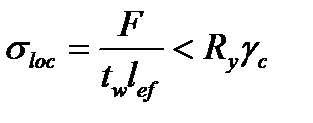 ;
;
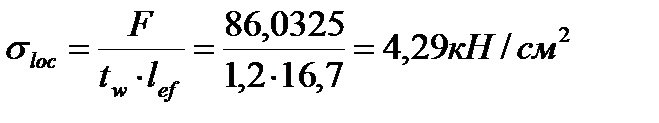 ,
,
де 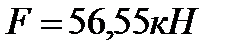 - опорна реакція балки настилу;
- опорна реакція балки настилу;
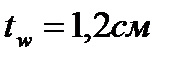 - товщина стінки головної балки;
- товщина стінки головної балки; 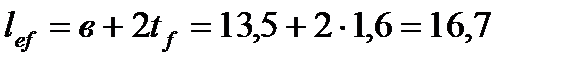 .
.
b - ширина полиці балки настилу;
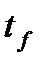 - товщина полиці головної балки.
- товщина полиці головної балки.
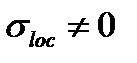 та
та 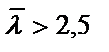 , необхідна перевірка місцевої стійкості в усіх відсіках стінки. Перевірку стійкості виконуємо у 1-ому відсіку та відсіку, де змінюється переріз та одночасно діють
, необхідна перевірка місцевої стійкості в усіх відсіках стінки. Перевірку стійкості виконуємо у 1-ому відсіку та відсіку, де змінюється переріз та одночасно діють 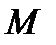 і
і 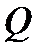 . Це 2-й відсіквід опори.
. Це 2-й відсіквід опори.
Перевірка місцевої стійкості:
1-1, на відстані 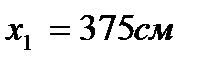 від опори, де прикладена зосереджена сила і
від опори, де прикладена зосереджена сила і 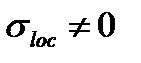
2-2, на відстані 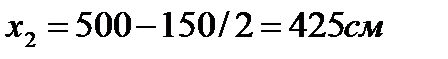 .
.
В переріз1-1 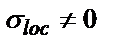 визначаємо розрахункові зусилля:
визначаємо розрахункові зусилля:
х1=375мм
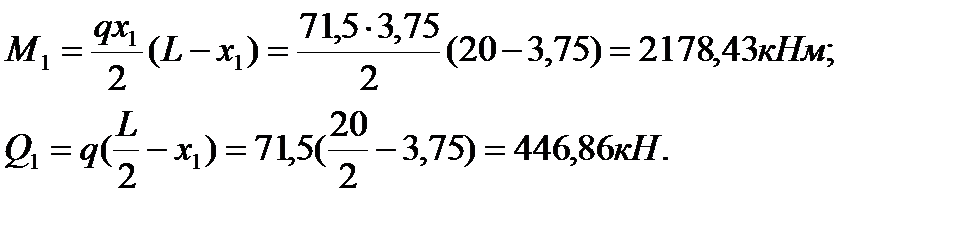
Нормальні стискаючі напруження в стінці на рівні її з’єднання із стиснутим поясом обчислюємо за формулою:
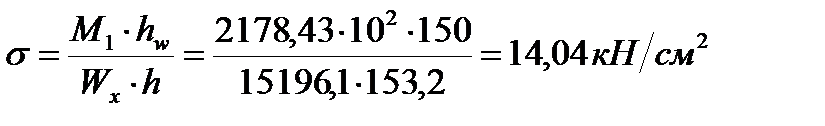
Середні дотичні напруження за формулою:
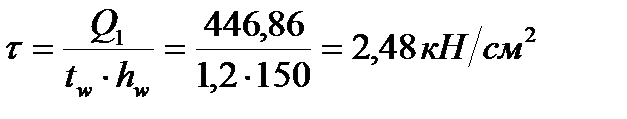 .
.
Знаходимо 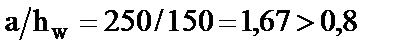 і коефіцієнт
і коефіцієнт 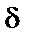 :
:
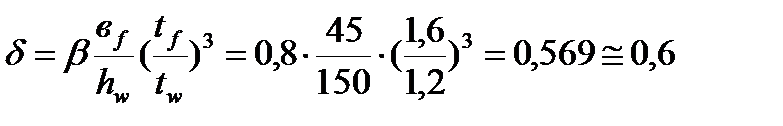 .
.
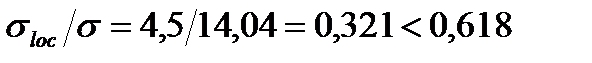 .
.
Критичні нормальні напруження обчислюємо:
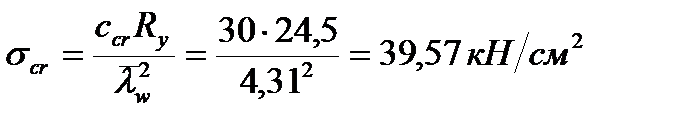 ,
, 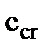 =30
=30
де 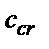 =30- визначаємо за [1, табл.21], в залежності від
=30- визначаємо за [1, табл.21], в залежності від 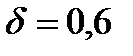
Мал. визначення локальних напружень
Місцеві нормальні критичні напруження за [1, формула (80), та п.7.6*,в]: 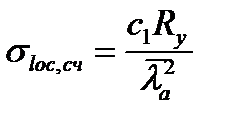 ,
,
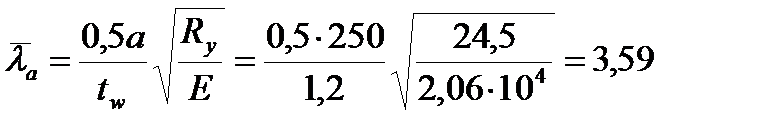 ;
;
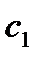 - коефіцієнт, який приймається за [1, табл.23] в залежності від
- коефіцієнт, який приймається за [1, табл.23] в залежності від 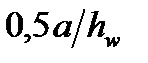 і значення
і значення 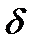 .
.
Якщо 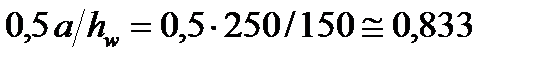 →
→ 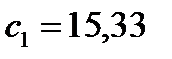 →
→
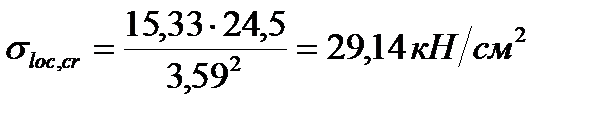 .
.
Критичні дотичні напруження знаходимо за формулою: 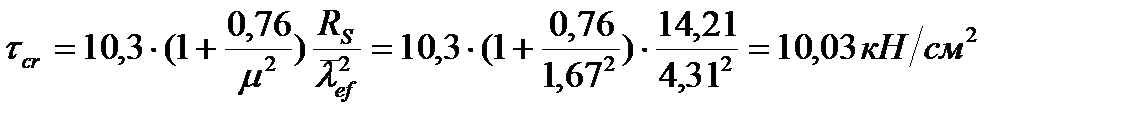 .
.
де, якщо більший бік відсіку 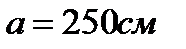 і менший
і менший 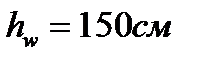 :
:
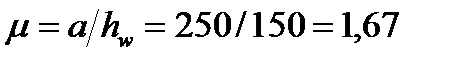 ;
;
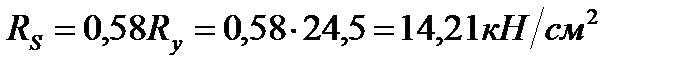 .
.
Тепер перевіряємо місцеву стійкість стінки в перерізі 1-1 за формулою:
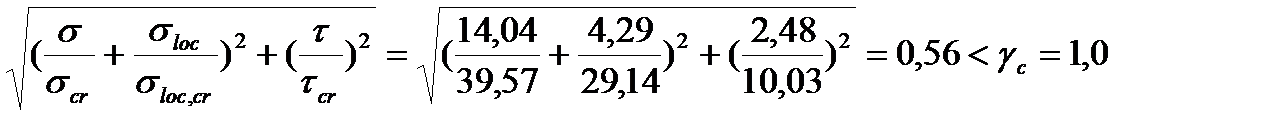
Місцева стійкість стінки в перерізі 1-1 забезпечена.
В перерізі 2-2 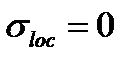 розрахункові зусилля визначаємо за формулами:
розрахункові зусилля визначаємо за формулами:
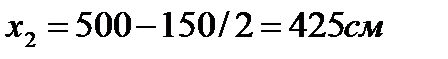
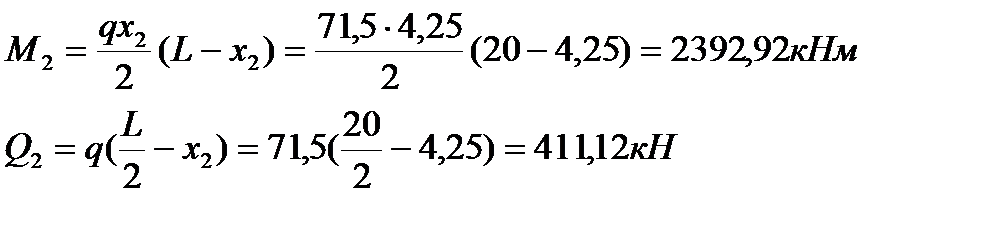
Нормальні стискаючі і середні дотичні напруження:
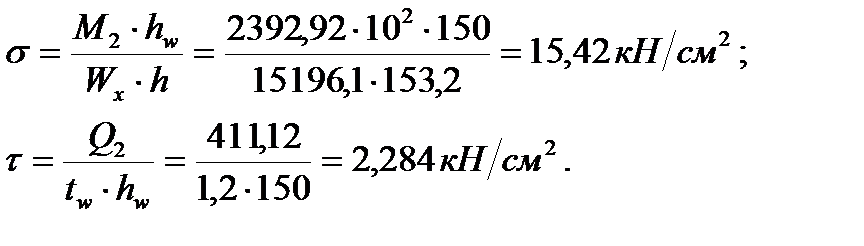
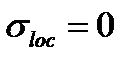
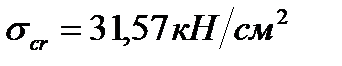 ;
; 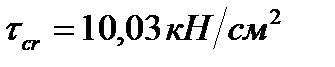 .
.
Перевіряємо місцеву стійкість стінки в перерізі 2-2 за формулою:
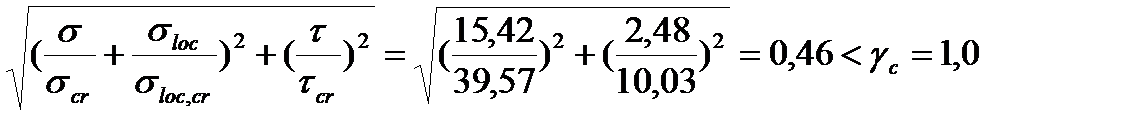 .
.
 2020-10-12
2020-10-12 148
148








