| Multiple Regression Results (Step 2)
Dependent: Ta Multiple R = ,83862642 F = 42,66617
R?= ,70329427 df = 2,36
No. of cases: 39 adjusted R?= ,68681061 p = ,000000
Standard error of estimate:,258442309
Intercept: 265,65336373 Std.Error: 2,927368 t(36) = 90,748 p = 0,0000
|
Результаты анализа в пакете «Статистика» позволяют сделать те же выводы, что и анализ в MS Excel. Были получены те же параметры и уравнение регрессионной модели, что логично, т.к. для анализа использовались идентичные исходные данные.
Уравнение модели имеет следующий вид:
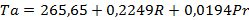
Таблица 8 – Характеристики регрессии в пакете «Статистика»
| Regression Summary for Dependent Variable: Ta (Spreadsheet1) R=,83862642 R?=,70329427 Adjusted R?=,68681061 F(2,36)=42,666 p | ||||||
| b* | Std.Err. - of b* | b | Std.Err. - of b | t(36) | p-value | |
| Intercept | 265,6534 | 2,927368 | 90,74820 | 0,000000 | ||
| R=(LFD+SFD)-(LFU+SFU) | 0,778594 | 0,098524 | 0,2249 | 0,028455 | 7,90259 | 0,000000 |
| Pr | 0,736751 | 0,098524 | 0,0194 | 0,002597 | 7,47789 | 0,000000 |
Можно выделить следующие критерии качества данной модели:
· Минимальное значение t-статистки параметра = 7,48, в то время как критическое значение (tкр) для 0,05 уровня надежности с данным количеством степеней свободны = 2,0281. Соответственно все параметры модели статистически значимы.
· Коэффициент детерминации R2 > 0,7, что говорит о хорошем уровне объяснения зависимости данной моделью.
· Модель адекватна данным по F-критерию. Рассчитанный F-критерий имеет значение 42,66617, в то время как критическое значение F-критерия = 3,2594.
· Стандартная ошибка модели = 0,2584 К, что меньше 0,67 * 0,46 = 0,31 К;
· Независимых переменных всего 2 штуки.
Значения, полученные в ходе наблюдения и значения, полученные в результате расчета регрессионной модели, были помещены в таблицу 9.
Таблица 9 – Наблюдаемые и расчетные показатели зависимой переменной в пакете «Статистика»
| № | Observed (К) | Predicted (К) | Residual (К) |
| 1 | 288,5767 | 288,6357 | -0,0591 |
| 2 | 289,6408 | 289,0563 | 0,5845 |
| 3 | 289,1925 | 289,0524 | 0,1401 |
| 4 | 288,7708 | 289,0124 | -0,2416 |
| 5 | 289,4400 | 289,2714 | 0,1686 |
| 6 | 289,2742 | 289,4560 | -0,1818 |
| 7 | 289,4367 | 289,4311 | 0,0056 |
| 8 | 289,5567 | 289,4003 | 0,1564 |
| 9 | 289,0483 | 289,3976 | -0,3493 |
| 10 | 289,6042 | 289,6473 | -0,0432 |
| 11 | 288,7658 | 289,1118 | -0,3459 |
| 12 | 289,3983 | 289,5025 | -0,1041 |
| 13 | 289,4267 | 289,6709 | -0,2442 |
| 14 | 289,9033 | 289,7919 | 0,1114 |
| 15 | 288,9183 | 288,9013 | 0,0170 |
| 16 | 288,7725 | 289,0330 | -0,2605 |
| 17 | 289,3208 | 289,7527 | -0,4319 |
| 18 | 289,3675 | 289,5037 | -0,1362 |
| 19 | 289,3367 | 289,1257 | 0,2109 |
| 20 | 289,8708 | 289,4689 | 0,4019 |
| 21 | 289,5333 | 289,8709 | -0,3376 |
| 22 | 289,3483 | 289,5942 | -0,2459 |
| 23 | 290,1167 | 289,6126 | 0,5041 |
| 24 | 289,4758 | 289,8706 | -0,3948 |
| 25 | 288,9708 | 288,9944 | -0,0236 |
| 26 | 289,4658 | 289,2903 | 0,1755 |
| 27 | 290,0008 | 289,9624 | 0,0384 |
| 28 | 289,8308 | 289,9199 | -0,0890 |
| 29 | 289,8550 | 290,0999 | -0,2448 |
| 30 | 289,3975 | 289,4898 | -0,0923 |
| 31 | 289,9708 | 289,6642 | 0,3066 |
| 32 | 289,9642 | 289,9227 | 0,0415 |
| 33 | 289,9200 | 289,7887 | 0,1313 |
| 34 | 289,9975 | 289,7751 | 0,2224 |
| 35 | 290,2042 | 289,9393 | 0,2648 |
| 36 | 289,8183 | 289,8127 | 0,0057 |
| 37 | 289,8325 | 289,9766 | -0,1441 |
| 38 | 290,3300 | 290,2026 | 0,1274 |
| 39 | 290,5800 | 290,2243 | 0,3557 |
Характеристики остатков регрессионной модели:
· Максимальное значение: 0,58 К;
· Минимальное значение: -0,43 К;
· Среднее значение: 0,00 К.
Значения аналогичны полученным в разделе 3.2.
На основании данных Таблицы 9 был построен график наблюдаемого и рассчитанного значения зависимой переменной Ta, приведенный на рисунке 4.
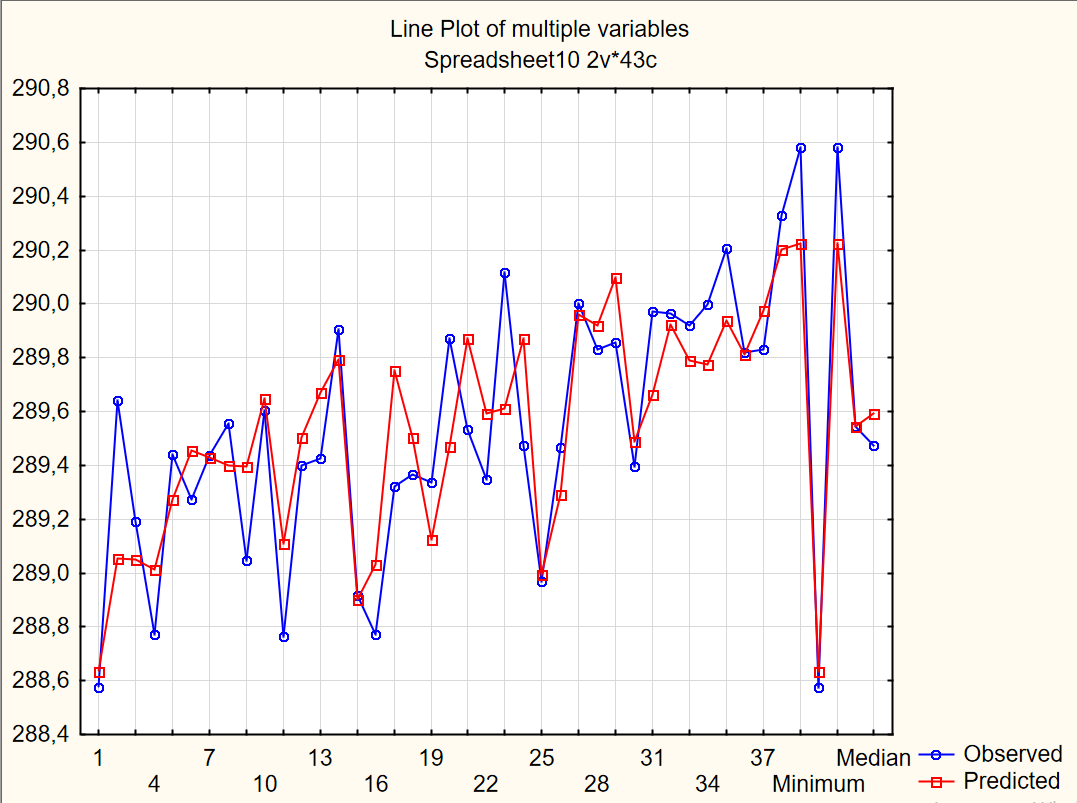
Рисунок 4 - График наблюдаемого и рассчитанного значения зависимой переменной Ta в пакете "Статистика"
 2020-10-12
2020-10-12 205
205








