3.1. а) 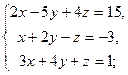
| б) 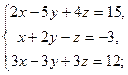
| в) 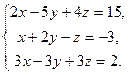
|
3.2. а) 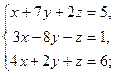
| б) 
| в) 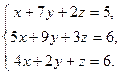
|
3.3. а) 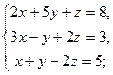
| б) 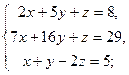
| в) 
|
3.4. а) 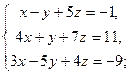
| б) 
| в) 
|
3.5. а) 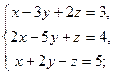
| б) 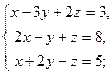
| в) 
|
3.6. а) 
| б) 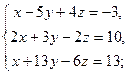
| в) 
|
3.7. а) 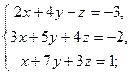
| б) 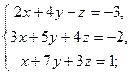
| в) 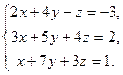
|
3.8. а) 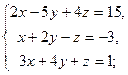
| б) 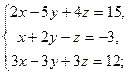
| в) 
|
3.9. а) 
| б) 
| в) 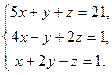
|
3.10. а) 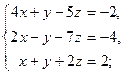
| б) 
| в) 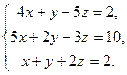
|
3.11. а) 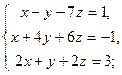
| б) 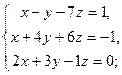
| в) 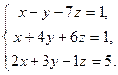
|
3.12. а) 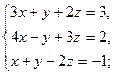
| б) 
| в) 
|
3.13. а) 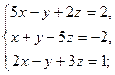
| б) 
| в) 
|
3.14. а) 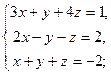
| б) 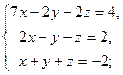
| в) 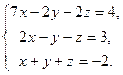
|
3.15. а) 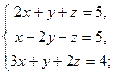
| б) 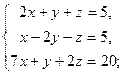
| в) 
|
3.16. а) 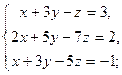
| б) 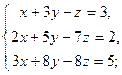
| в) 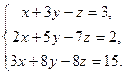
|
3.17. а) 
| б) 
| в) 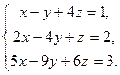
|
3.18. а) 
| б) 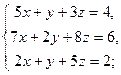
| в) 
|
3.19. а) 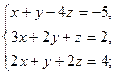
| б) 
| в) 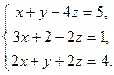
|
3.20. а) 
| б) 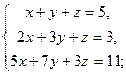
| в) 
|
3.21. а) 
| б) 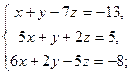
| в) 
|
3.22. а) 
| б) 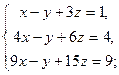
| в) 
|
3.23. а) 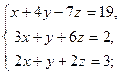
| б) 
| в) 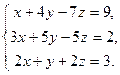
|
3.24. а) 
| б) 
| в) 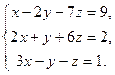
|
3.25. а) 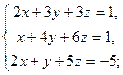
| б) 
| в) 
|
3.26. а) 
| б) 
| в) 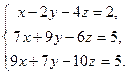
|
3.27. а) 
| б) 
| в) 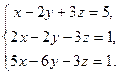
|
3.28. а) 
| б) 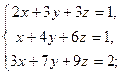
| в) 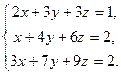
|
3.29. а) 
| б) 
| в) 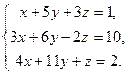
|
3.30. а) 
| б) 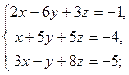
| в) 
|
Решить однородную систему линейных уравнений.
4.1. 
| 4.10. 
|
4.2. 
| 4.11. 
|
4.3. 
| 4.12. 
|
4.4. 
| 4.13. 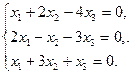
|
4.5. 
| 4.14. 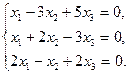
|
4.6. 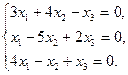
| 4.15. 
|
4.7. 
| 4.16. 
|
4.8. 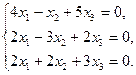
| 4.17. 
|
4.9. 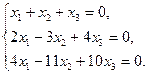
| 4.18. 
|
4.19. 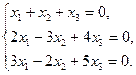
|
4.25. 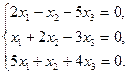
|
4.20. 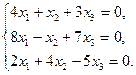
| 4.26. 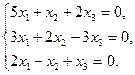
|
4.21. 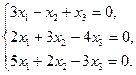
| 4.27. 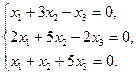
|
4.22. 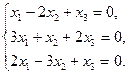
| 4.28. 
|
4.23. 
| 4.29. 
|
4.24. 
| 4.30. 
|
5. Исследовать систему на совместность с помощью теоремы Кронекера-Капелли.
5.1.  5.4.
5.4. 
5.2. 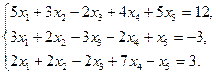 5.5.
5.5. 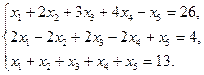
5.3.  5.6.
5.6. 
5.7.  5.14.
5.14. 
5.8.  5.15.
5.15. 
5.9.  5.16.
5.16. 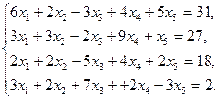
5.10. 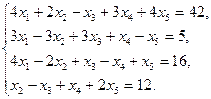 5.17.
5.17. 
5.11. 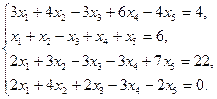 5.18.
5.18. 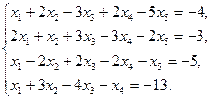
5.12. 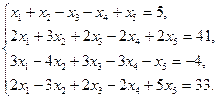 5.19.
5.19. 
5.13.  5.20.
5.20. 
5.21. 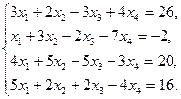 5.26.
5.26. 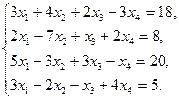
5.22. 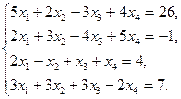 5.27.
5.27. 
5.23. 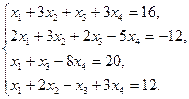 5.28.
5.28. 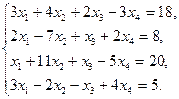
5.24. 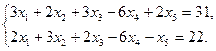 5.29.
5.29. 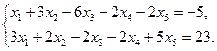
5.25. 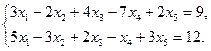 5.30.
5.30. 
Зачетное домашнее задание №2
Элементы векторной алгебры и аналитической геометрии
Даны четыре точки А, В, С и D.
Вычислить: а)  ; б)
; б)  ),
), 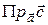 ;
;
в) в заданном треугольнике длину медианы
m и стороны 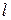 ;
;
г) площадь треугольника и его высоту h;
д) объём пирамиды ABCD и её высоту Н;
(точка Е – на медиане, F – основание высоты в треугольнике,
 2020-10-12
2020-10-12 112
112








