2014-02-04
737
Таблица 1
| Функция F и базисные неизвестные | Свободные члены | Свободные переменные | |||||
 | … |  | …. |  | |||
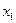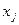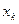| F |  |  | … |  | …. |  | |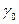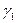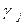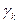
 |  |  | … |  | …. |  | |
| …. | … | … | …. | ||||
 |  |  | … |  | ….. |  | |
| …. | … | … | …. | ||||
 |  |  | … |  | ….. |  |
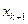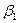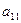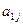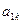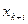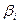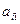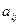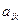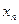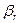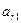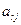4. С помощью симплекс-таблицы выясняют, имеет ли вообще данная задача решение (совместна ли система) и является ли выбранный план опорным.
Если все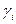 
положительны, то при положительных 
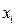линейная функция F неограниченна снизу и оптимального решения задачи не существует. Опорным же план будет тогда когда все 
.
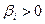5. Рассматривают те из свободных неизвестных, которые в форме (8) стоят с положительными коэффициентами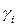
и из них выбирают какую-либо одну (например 
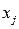). Если вс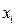е кроме 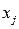, придать нулевые значения, а 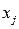увеличивать, то F будет уменьшаться. Причем 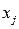можно увеличивать до тех пор, пока какое-либо 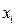не станет нулевым (из системы (7)).
Если все свободные неизвестные, кроме 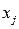, равны нулю то из системы (7) остается:
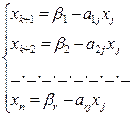(9)
Все базисные неизвестные, у которых коэффициент меньше нуля при увеличении 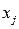убывать не будут. Будут, убывать, а следовательно превращаться в нуль, только те неизвестные, у которых коэффициент при 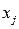больше нуля.
Базисная неизвестная 
обратится в нуль только при
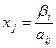
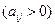
Причем первая превратится в нуль та базисная неизвестная, для которой отношение
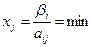
остальные будут еще положительными.
Коэффициент 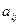называется разрешающим элементом (его подчеркивают). Строка и столбец с разрешающим элементом называют разрешающим.
Увеличение значения 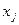до величины 
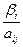перемещают нас от исходной опорной точки к новой. При этом функция F уменьшается до величины 
.
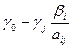С целью дальнейшего уменьшения F составляют новую симплекс-таблицу, в которой в качестве свободных неизвестных будут прежние, а вместо 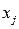войдет . Затем все повторяется.
Правило перехода к новой симплекс-таблице:
Для составления новой симплекс-таблицы при переходе от 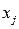к нужно:
· Разрешающий элемент заменить на обратную ему величину (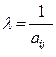
);
· Все остальные элементы разрешающей строки разделить на разрешающий элемент (умножить на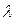 
);
· Все элементы разрешающего столбца, кроме самого разрешающего элемента, тоже разделить на разрешающий элемент (умножить на 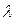) и перед каждым сменить знак на противоположный (умножить на -1);
· Для каждой из клеток, не стоящей в разрешающих строках и столбцах, получить произведение числа, стоящей в верхней части пересечения разрешающей строки со столбцом данной клетки, на число, стоящей в нижней части пересечения разрешающего столбца со строкой взятой клетки.
В таблице 2 с помощью этих правил заполнены нижние части клеток разрешающих строк и столбцов новыми элементами, а всех остальных клеток- соответствующими слагаемыми новых элементов.
 | … | | … | | ||
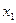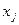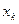| F |  |  | …. |  | …. |  |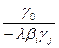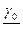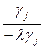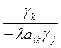
 |  |  |  | ….. |  | |
| …. | ….. | …. | …. | …. | …. | …. |
 |  |  | … |  | … |  |
| … | … | … | … | … | … | … |
| |  |  | … |  | … |  |
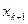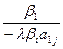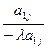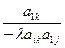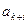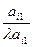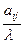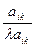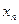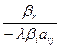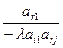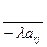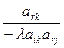После применения перечисленных правил и использование слагаемых новых элементов клеток, не входящих в разрешающую строку и столбец, получается симплекс-таблица для нового набора свободных неизвестных.
Теперь можно продолжить работу по той же схеме дальше, пока в результате конечного числа шагов не появится симплекс-таблица, в первой строке которой все коэффициенты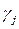 
, коме 
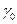не станут отрицательными. Последнее будет означать, что получено оптимальное решение задачи линейного программирования, при котором целевая функция F минимизирована.
