VI. Решающее правило для принятия диагноза

Решающее правило — правило, в соответствии с которым принимается решение о диагнозе. В методе Байеса ОД с комплексом ДП 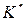относится к диагнозу с наибольшей вероятностью

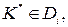если 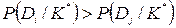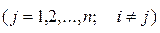. (15)

Данное правило уточняется пороговым значением для вероятности диагноза

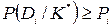, (16)

где 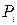- уровень распознавания диагноза , .

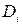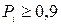Если 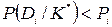, то диагноз не принимается (отказ от распознавания).

При равной вероятности диагнозов принимается тот, при котором комплекс ДП 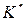встречается чаще. Такое решающее правило соответствует методу максимального правдоподобия и является частным случаем метода Байеса при одинаковых априорных вероятностях диагнозов. При этом «частые» и «редкие» диагнозы равноправны.

VII. Пример применения метода Байеса

Вернемся к примеру о работе газовой турбины.

Пусть при наблюдении за газотурбинным двигателем проверяются два ДП:

1. 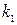- повышение температуры газа за турбиной более чем на ;

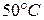2. 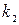- увеличение времени выхода на максимальную частоту вращения более чем на 5с.

Появление этих признаков связано с двумя состояниями:

1. состояние 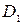- неисправность топливного регулятора;

2. состояние 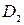- увеличение радиального зазора в турбине.

Статистические данные:

1. при нормальном состоянии двигателя (состояние 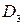) признак 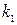не наблюдается, а признак 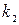наблюдается в 5% случаев;

2. 80% двигателей вырабатывают ресурс в нормальном состоянии, 5% двигателей имеют состояние 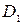и 15% состояние ;

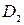3. признак 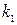встречается при состоянии 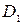в 20%, а при состоянии 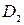в 40% случаев;

4. признак 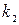при состоянии 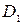встречается в 30%, а при состоянии 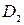- в 50% случаев.

Сведем эти данные в диагностическую матрицу (таблица 2).

Таблица 2 – Вероятности признаков и априорные вероятности состояний

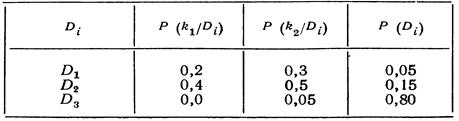
Найдем сначала вероятности состояний двигателя 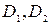и 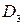, когда обнаружены оба признака 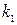и 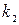. Для этого, считая признаки независимыми, применим формулу (13).

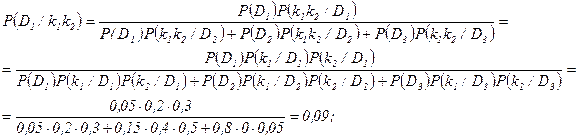
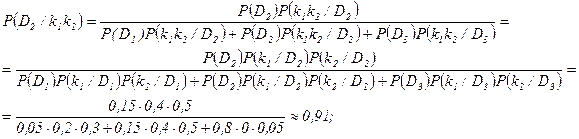
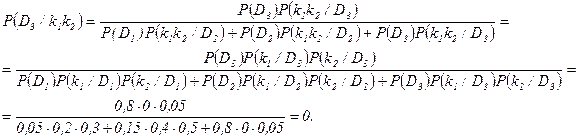
Задача является несложной, если одновременно появляются оба признака и . В случае, когда признаки появляются не одновременно, задача решается следующим образом:

для расчета применяют также формулу (13), но значение 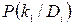заменяют на 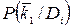, т.е. вероятности наличия признаков заменяют на вероятности отсутствия данных признаков

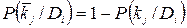(17)

В этом случае, согласно предыдущим выкладкам, получим

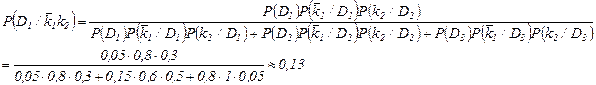
и аналогично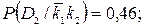

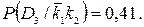
Вычислим вероятности состояний в том случае, когда оба признака отсутствуют. Аналогично предыдущим выкладкам получим

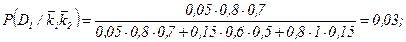
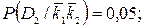
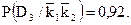
Занесем полученные результаты в диагностическую матрицу (таблица 3).

Таблица 3 – Определение наиболее вероятного диагноза

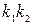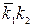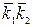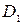	0,09	0,13	0,03
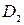	0,91	0,46	0,05
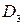		0,41	0,92

Проанализируем матрицу:

1. при наличии признаков 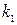и 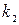в двигателе с вероятностью 0,91 имеется состояние 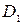, т. е. увеличение радиального зазора;

2. при отсутствии обоих признаков наиболее вероятно нормальное состояние (вероятность 0,92);

3. при отсутствии признака 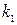и наличии признака 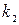вероятности состояни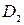й и 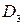примерно одинаковы (0,46 и 0,41) и для уточнения состояния двигателя требуется проведение дополнительных обследований.