Простейшая корпускулярная модель, в которой пористая среда моделируется упаковкой шаров постоянного диаметра, называется фиктивным грунтом или фиктивной пористой средой.
Простейшая капиллярная модель, в которой пористая среда моделируется капиллярными трубками постоянного диаметра, уложенными с постоянным периодом, называется идеальным грунтом или идеальной пористой средой.
Наиболее распространенные модели фиктивного грунта получаются при наиболее плотных упаковках шаров. Две основные упаковки – кубическая и гексагональная получаются следующим образом: первый плоский слой уложен так, что каждый шар касается шести соседних, каждый шар второго слоя помещается в углубление межу тремя шарами первого слоя (рис. 1.3). При наложении третьего слоя возможны два варианта. При кубической упаковке каждый шар третьего слоя лежит на трех шарах второго слоя таким образом, что под шаром третьего слоя нет шара первого слоя. При гексагональной упаковке каждый шар третьего слоя лежит на трех шарах второго, но под каждым шаром третьего слоя оказывается шар первого слоя.
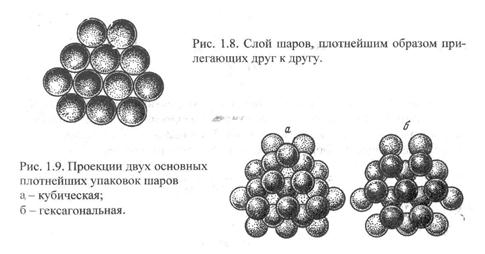
Рис. 1.3. Упаковки шаров: а) кубическая, б) гексагональная
Кроме указанной, наиболее плотной упаковки с кубической симметрией рассматривают и такую упаковку, когда в первом слое каждый шар касается только четырех шаров, а все последующие слои повторяют первый. Такую упаковку называют рыхлой кубической упаковкой.
Для капиллярных моделей идеального грунта наиболее простые модели получаются при взаимно перпендикулярном расположении капилляров.
Применение идеальных и фиктивных грунтов позволяет упростить структуру порового пространства, находить аналитические формулы для упрощенных пористых сред, и обобщать полученные соотношения на реальные пористые среды.
Рассмотрим соотношения для фиктивного грунта.
Для фиктивного грунта существует соотношение, связывающее удельную поверхность с пористостью упаковки m и диаметром шаров D. Возьмем объем, в котором имеется n шаров. Весь объем можно представить как сумму пустот и шаров:

Из полученного равенства получаем 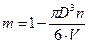 (1*)
(1*)
Удельная поверхность равна площади поверхности одного шара, умноженной на число шаров в упаковке:
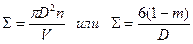 (2*)
(2*)
Для проницаемости пористых сред используется следующая формула:
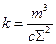 ,
,
где с – число Кармана. Для упаковок шаров с = 5.
Подставляя это выражение в (2*) получаем выражение для проницаемости фиктивного грунта
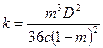 (3*)
(3*)
Для идеального грунта структура порового пространства такова, что допускает аналитическое определение основных фильтрационно-емкостных характеристик. Для представления идеального грунта использовались разные схемы элементарных ячеек – одномерные (рис. 1.4) и трехмерные (рис.)
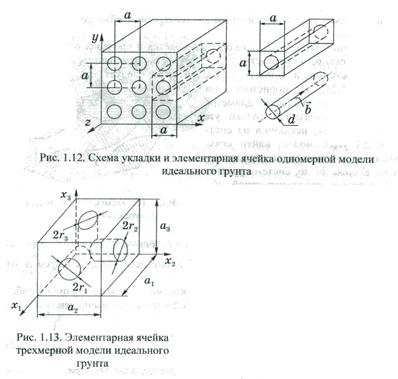
Рис. 1.4. Схема укладки и элементарная ячейка одномерной и трехмерной модели идеального грунта.
Вычислим значения пористости, просветности, удельной поверхности и проницаемости для идеального грунта, образованного тремя системами взаимно перпендикулярных капилляров. Диаметры капилляров примем равным dα = 2rα, периоды укладки - аα, α = 1, 2, 3.
Все вычисления проводятся на элементарной ячейке, образованной тремя взаимно перпендикулярными периодами укладки. Введем декартову систему координат, оси которой параллельны осям симметрии капилляров, которые в свои очередь параллельны периодам укладки. Значения индексов в обозначении (α) соответствует номеру оси координат, которой параллельны капилляр и период. Тогда пористость, просветность, удельная поверхность и проницаемость определяются как
 ,
,  ,
, 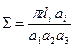 ,
, 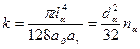 (4*)
(4*)
В (4*) подразумевается суммирование по повторяющимся латинским индексам i, греческие индексы α, β, γ образуют циклическую перестановку цифр 1, 2, 3.
Истинная средняя скорость движения флюида (в капилляре) получается из вывода уравнения Бернулли и формулы Дарси-Вейсбаха для ламинарного течения в круглой трубе
 ,
,
где l – длина капилляра между сечениями 1 – 2, μ – динамическая вязкость.
Скорость фильтрации для одномерной модели грунта  . (5*)
. (5*)
(5*) совпадает по форме с законом Дарси.
Физический смысл (5*): 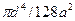 - представляет собой проницаемость «одномерного» идеального грунта. При этом первый множитель
- представляет собой проницаемость «одномерного» идеального грунта. При этом первый множитель 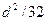 задает «проводимость» капилляров, и его вид определяется формой поперечного сечения каналов. Здесь используются цилиндрические трубки кругового сечения. Могут быть, например, плоские щели или капилляры эллиптического сечения. Второй множитель
задает «проводимость» капилляров, и его вид определяется формой поперечного сечения каналов. Здесь используются цилиндрические трубки кругового сечения. Могут быть, например, плоские щели или капилляры эллиптического сечения. Второй множитель  задает просветность, которая выступает в качестве масштаба осреднения.
задает просветность, которая выступает в качестве масштаба осреднения.
Следовательно, проницаемость является комплексной характеристикой пористой среды, учитывающей как форму и размеры поперечного сечения поровых каналов, так и их концентрацию в среде.
Часто в расчетные формулы для определения проницаемости включают коэффициент извилистости α, который равен отношению длины проводящего порового канала или «истинного» пути флюида в образце (траектории меченой частицы) к длине образца. В различных модификациях модели одномерного идеального грунта α = 1 – 3.
Для трехмерной модели равенство (5*) сохраняется с той лишь разницей, что проставляются индексы, для того чтобы указать какому капилляру соответствует формула.

где индексы α, β, γ образуют циклическую перестановку.
Коэффициент проницаемости в трехмерной модели идеальной пористой среды

Из соотношения (4*) следует, что  и равенство просветности и пористости выполняется лишь при
и равенство просветности и пористости выполняется лишь при 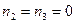 , т.е. только случае одномерной модели идеального грунта. Таким образом, равенство m = n выполняется только для одномерной модели идеального грунта.
, т.е. только случае одномерной модели идеального грунта. Таким образом, равенство m = n выполняется только для одномерной модели идеального грунта.
Диаметр пор или диаметр капилляров в модели идеального грунта в общем виде
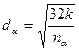 (6*)
(6*)
При условии m = n 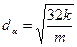 (7*)
(7*)
В трехмерной модели идеального грунта равенство (7*) не выполняется. Для перехода от просветности к пористости вводят структурный коэффициент 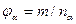 .
.
Тогда  (8*)
(8*)
Если в трехмерной модели идеального грунта предположить, что 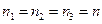 , m = 3n,
, m = 3n,  то получим
то получим 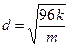 .
.
В общем случае значение φ ограничено только снизу – φ ≥ 1,и значение структурного коэффициента может определяться в широком диапазоне.
Для моделирования пористых сред могут использоваться разнообразные статистические модели с хаотично уложенными сферами, со случайными решетками, со сложной геометрией капиллярных каналов.
1.3. Скорость фильтрации, Линейный закон Дарси. /ввести нумерацию формул/
В теории фильтрации движение жидкости или газа через пористую среду рассматривается не с точки зрения движения потоков по отдельным извилистым микроскопическим каналам, а распространяют расход жидкости или газа на всю поперечную площадь пористой среды. Эта фиктивная скорость называется скоростью фильтрации. Истинные скорости движения в отдельных каналах могут значительно превышать скорость фильтрации. В связи с этим все законы фильтрации, устанавливающие связь между скоростью фильтрации, градиентом давления и параметрами пористой среды и жидкости, носят статический характер.
При изучении фильтрационного потока удобно отойти от размеров пор и их формы, допустив, что жидкость движется сплошной массой, заполняя весь объем пористой среды, включая пространство, занятое скелетом породы.
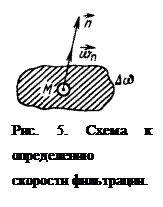
Основной характеристикой фильтрационного движения служит вектор скорости фильтрации ω, который определяется следующим образом. Выберем произвольную точку М пористого пласта, через который фильтруется жидкость, и выделим в нем элементарную площадку Sm (рис. 1.4). Через выделенную площадку в единицу времени протекает масса жидкости ΔQm (элементарный массовый расход).
Скорость фильтрации в пределах площадки можно выразить в виде
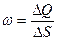 . (3)
. (3)
Скорость фильтрации в данной точке пласта 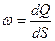 , (4)
, (4)
где 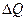 - объемный расход жидкости в фильтрационном потоке в единицу времени через площадку
- объемный расход жидкости в фильтрационном потоке в единицу времени через площадку 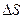 полного живого сечения пласта (мысленно предполагается, что жидкость движется по всему сечению пласта, т.е. при отсутствии самой породы).
полного живого сечения пласта (мысленно предполагается, что жидкость движется по всему сечению пласта, т.е. при отсутствии самой породы).
Величина ω имеет размерность скорости (м/с в СИ) и обладает свойствами вектора. Скорость фильтрации можно рассматривать как вектор. Если в данной точке области фильтрации вращать элементарную площадку и восстанавливать нормали, соответствующие наибольшему расходу, то нормаль и будет направлением вектора скорости фильтрации.
Массовый расход в выражении (3, 4) делится на полную площадь ΔS, а не на ее часть, занятую порами. Поэтому, очевидно, что скорость фильтрации не является действительной средней скоростью движения в живом сечении фильтрационного потока.
Установлена связь между скоростью фильтрации и средней скоростью движения жидкости в порах
 , (5)
, (5)
где  - коэффициент пористости, u - средняя скорость движения жидкости в порах.
- коэффициент пористости, u - средняя скорость движения жидкости в порах.
Поскольку 0 < m < 1, то скорость фильтрации ω меньше действительной средней скорости u течения флюида.
Таким образом, при введении скорости фильтрации ω рассматривается некоторый фиктивный фильтрационный поток, в котором расходы через любое сечение равны реальному расходу флюида, поля давлений фиктивного и реального потока идентичны, а сила сопротивления фиктивного потока равна реальной силе сопротивления. При этом принимается, что скорость фильтрации непрерывно распределена по объему и связана со средней скоростью действительного движения равенством (5).
Основное соотношение теории фильтрации - закон фильтрации устанавливает связь между вектором скорости фильтрации и тем полем давления, которое вызывает фильтрационное течение. Первые экспериментальные наблюдения за движением
воды в трубах, заполненных песком, провели французские инженеры А. Дарси и Ж. Дюпюи (1856 г.). Этими работами было положено начало теории фильтрации. Именем Дарси назван основной закон фильтрации – закон Дарси (или линейный закон фильтрации). Дарси создал первую совершенную систему водоснабжения в Европе.
Анри Дарси исследовал течение воды через вертикальные песчаные фильтры, что требовалось для нужд водоснабжения г. Дижона. В результате тщательно проведенных экспериментов он установил получившую широкую известность экспериментальную формулу
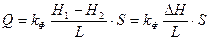 (6)
(6)
где Q – объемный расход жидкости через песчаный фильтр, длина которого L, площадь сечения S, ΔН = Н1 – Н2 – разность гидравлических напоров воды над фильтром и у его основания, kф – коэффициент пропорциональности.
Коэффициент пропорциональности в выражении (6) еще называют коэффициент фильтрации (первоначально коэффициент водопроницаемости). Коэффициент фильтрации зависит от свойств пористой среды и свойств фильтрующейся жидкости. Наибольшее влияние на этот коэффициент оказывают размеры частиц породы. Величина этого коэффициента также зависит от формы частиц, степени шероховатости их поверхности, пористости среды, вязкости жидкости.
Скорости фильтрации очень малы (порядка 10-4 – 10-5 м/с и менее), поэтому скоростными напорами при вычислении гидравлических напоров в выражении (6) пренебрегают:
 (7)
(7)
В выражении (7) используются обозначения гидромеханики: υα – средние скорости в капилляре, αi – коэффициенты Кориолиса (в нашем случае α1 = α2 = 2), р – давление, z – геометрический напор, ρ – плотность жидкости, g – ускорение свободного падения.
 2014-02-02
2014-02-02 6610
6610








