Доказательство

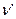Пусть и 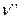- характеристические векторы множеств А' и А" соответственно. Если А' = А", то для всякого i имеем 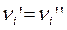. Отсюда следу­ет, что 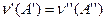. Наоборот, если 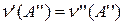, то для всякого i имеем 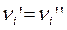. По определению характеристического вектора, если 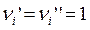, то 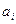принадлежит как множеству 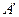, так и множеству 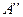, а если 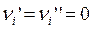, то элемент 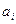не принадлежит ни тому ни другому подмножеству. Отсюда следует, что подмножества А' и А" состоят из одних и тех же элементов, т.е. .

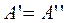Теорема доказана.

Следствие 1: Число различных подмножеств n-элементного множества равно 2".

Действительно, поскольку число компонент характеристического вектора равно n и каждая компонента может принимать одно из двух значений­ 0или 1, то число различных возможных характеристических векторов по ос­новному правилу комбинаторики равно 2 * 2 *... * 2 = 2".

Следствие 2:

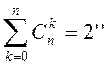
Действительно, поскольку 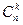– число различных k-элементных подмно­жеств n-элементного множества, то сумма всех таких чисел составляет число всех подмножеств данного n-элементного множества.