Поиск в ширину

6 Пометить все вершины как новые;

7 for 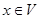do if 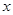новая then BFS(x).

Если граф задан списками смежности, то внутренний цикл в строке 4 процедуры BFS повторяется 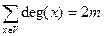раз. Кроме того, цикл в строке 7 повторяется n раз. Поэтому общая трудоемкость поиска в ширину оценивается как 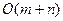. Если же граф задан матрицей смежности, то для сканирования окрестности вершины (строка 4) необходимо полностью просмотреть соответствующую строку этой матрицы и общая трудоемкость будет .

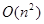Рассмотрим примеры применения поиска в ширину для решения конкретных задач.

Компоненты связности. Рассмотрим задачу выявления компонент связности графа. Ответ нужно получить в виде таблицы, в которой для каждой вершины 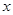должен быть указан номер компоненты 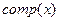, которой эта вершина принадлежит. Для решения этой задачи достаточно ввести переменную c со значением, равным текущему номеру компоненты, и каждый раз при посещении новой вершины x присваивать значение 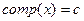. Значение c первоначально устанавливается равным 0 и модифицируется при каждом вызове процедуры BFS.

Кратчайшие пути и расстояния. Допустим, поиск в ширину выполняется на связном графе. Каркас, образованный прямыми ребрами, можно рассматривать как корневое дерево с корнем в стартовой вершине. Оно называется BFS-деревом. В процессе обхода легко построить таблицу отцов 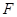, задающую это дерево: достаточно при посещении вершины 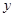при активной вершине 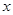присвоить значение 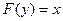. BFS-дерево с данным корнем не единственно, оно зависит от того, в каком порядке рассматриваются ребра, инцидентные активной вершине. Но все BFS-деревья обладают одним свойством, на котором основаны важнейшие применения поиска в ширину. Корневой каркас связного графа называется деревом кратчайших путей, если путь от любой вершины до корня в этом каркасе является кратчайшим путем между этими вершинами во всем графе.

Теорема о BFS-дереве. Любое BFS-дерево является деревом кратчайших путей.

Таким образом, однократным выполнением поиска в ширину можно найти кратчайшие пути и расстояния от данной вершины до всех остальных.

Центр дерева. Центр дерева можно найти следующим образом. Выберем в данном дереве произвольную вершину 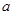. Выполнив поиск в ширину из вершины 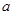, найдем наиболее удаленную от нее вершину 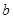. Выполнив второй раз поиск в ширину со стартом в вершине 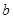, найдем наиболее удаленную от нее вершину 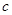. Центр пути, соединяющего 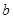и 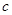, является центром всего дерева.