Циклы – очень важная часть структуры графа, с ними приходится иметь дело при решении многих задач. В графе может быть очень много циклов (см. задачу 5.15), поэтому полезно иметь средства для компактного описания множества всех циклов данного графа и манипулирования ими. Одно из наиболее удобных средств такого рода предоставляет аппарат линейной алгебры.
Далее будем рассматривать графы с фиксированным множеством вершин V. Буквой O будем обозначать пустой граф:  .
.
Суммой по модулю 2 (в дальнейшем в этом разделе будем называть ее просто суммой) двух графов 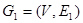 и
и 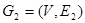 называется граф
называется граф 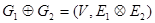 , где
, где 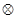 обозначает симметрическую разность множеств.
обозначает симметрическую разность множеств.
Следующие свойства введенной операции очевидны или легко проверяются.
1) Коммутативность: 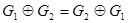 для любых
для любых 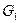 и
и 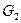 .
.
2) Ассоциативность: 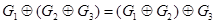 для любых
для любых 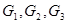 .
.
3) 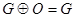 для любого G.
для любого G.
4) 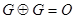 для любого G.
для любого G.
Отсюда следует, что множество всех графов с множеством вершин V образует абелеву группу относительно операции сложения по модулю 2. Нейтральным элементом («нулем») этой группы служит граф O, а противоположным к каждому графу является сам этот граф. Уравнение 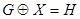 с неизвестным X и заданными графами G и H имеет единственное решение
с неизвестным X и заданными графами G и H имеет единственное решение 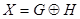 . Благодаря свойству ассоциативности мы можем образовывать выражения вида
. Благодаря свойству ассоциативности мы можем образовывать выражения вида 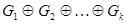 , не используя скобок для указания порядка действий. Легко понять, что ребро принадлежит графу
, не используя скобок для указания порядка действий. Легко понять, что ребро принадлежит графу 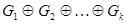 тогда и только тогда, когда оно принадлежит нечетному количеству из графов
тогда и только тогда, когда оно принадлежит нечетному количеству из графов 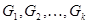 .
.
Рассмотрим множество из двух элементов {0,1}. Оно является полем относительно операций умножения и сложения по модулю 2. Определим операцию умножения элементов этого поля на графы: 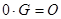 ,
, 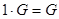 для любого графа G. Множество всех графов с множеством вершин V при введенных операциях сложения графов и умножения на элементы поля является линейным векторным пространством (т. е. подчиняется аксиоматике таких пространств).
для любого графа G. Множество всех графов с множеством вершин V при введенных операциях сложения графов и умножения на элементы поля является линейным векторным пространством (т. е. подчиняется аксиоматике таких пространств).
Зафиксируем некоторый граф 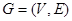 и рассмотрим множество всех его остовных подграфов. Это множество состоит из
и рассмотрим множество всех его остовных подграфов. Это множество состоит из  элементов, среди них сам граф G и граф
элементов, среди них сам граф G и граф 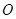 . Оно замкнуто относительно сложения графов и умножения на элементы поля, следовательно, является подпространством пространства всех графов. Его называют пространством подграфов графа G.
. Оно замкнуто относительно сложения графов и умножения на элементы поля, следовательно, является подпространством пространства всех графов. Его называют пространством подграфов графа G.
В пространстве подграфов можно естественным способом ввести координаты. Занумеруем ребра графа G: 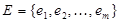 . Теперь остовному подграфу
. Теперь остовному подграфу 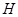 можно поставить в соответствие характеристический вектор
можно поставить в соответствие характеристический вектор 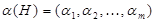 его множества ребер:
его множества ребер:
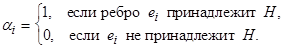
Получаем взаимно однозначное соответствие между множеством подграфов и множеством 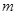 -мерных двоичных векторов. Сумме графов соответствует векторная (покоординатная) сумма по модулю 2 их характеристических векторов.
-мерных двоичных векторов. Сумме графов соответствует векторная (покоординатная) сумма по модулю 2 их характеристических векторов.
Далее в этом разделе слово «цикл» будем понимать несколько иначе, чем до сих пор.Именно, циклом графа G будемназывать его остовный подграф, у которого одна компонента связности является простым циклом, а остальные – изолированными вершинами. Остовный подграф, у которого степени всех вершин четны, называется квазициклом. Таким образом, любой цикл является квазициклом и граф О – квазицикл.
Теорема о квазициклах. Множество всех квазициклов данного графа замкнуто относительно сложения по модулю 2.
Из этой теоремы следует, что множество всех квазициклов графа G является подпространством пространства подграфов, оно называется пространством циклов графа.
Компактное представление линейного векторного пространства дает его базис. Базис пространства циклов называют просто базисом циклов. Построить базис циклов можно следующим образом. Выберем в графе G какой-нибудь каркас T. Пусть 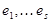 – все ребра графа G, не принадлежащие T. Если добавить к T ребро
– все ребра графа G, не принадлежащие T. Если добавить к T ребро 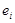 , то в полученном графе образуется единственный цикл
, то в полученном графе образуется единственный цикл 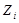 . Таким образом, получаем семейство из s циклов, они называются фундаментальными циклами относительно каркаса T.
. Таким образом, получаем семейство из s циклов, они называются фундаментальными циклами относительно каркаса T.
Теорема о фундаментальных циклах. Множество всех фундаментальных циклов относительно любого каркаса T графа G образует базис пространства циклов этого графа.
Из этой теоремы следует, что размерность пространства циклов графа равна числу ребер, не входящих в его каркас. Так как каркас содержит 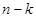 ребер, где k – число компонент связности графа, то эта размерность равна
ребер, где k – число компонент связности графа, то эта размерность равна 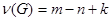 . Это число называют цикломатическим числом графа.
. Это число называют цикломатическим числом графа.
Каркас графа можно построить многими способам. Для построения базиса циклов графа особенно удобен поиск в глубину благодаря основному свойству DFS-дерева – каждое обратное ребро относительно этого дерева является продольным. Это означает, что из двух вершин такого ребра одна является предком другой в DFS-дереве. Каждое такое ребро в процессе поиска в глубину встретится дважды – один раз, когда активной вершиной будет предок, другой раз, когда ею будет потомок. В этом последнем случае искомый фундаментальный цикл состоит из рассматриваемого обратного ребра и участка пути в DFS-дереве, соединяющего эти две вершины. Но этот путь так или иначе запоминается в процессе обхода в глубину, так как он необходим для последующего возвращения. Если, например, для хранения открытых вершин используется стек, то вершины этого пути находятся в верхней части стека. В любом случае этот путь легко доступен и цикл находится без труда.
Хотя сам поиск в глубину выполняется за линейное от числа вершин и ребер время, решающее влияние на трудоемкость алгоритма оказывает необходимость запоминать встречающиеся циклы. Подсчитаем суммарную длину фундаментальных циклов, полученных с помощью поиска в глубину для полного графа с n вершинами. DFS-дерево в этом случае является простым путем, относительно него будет  цикла длины 3,
цикла длины 3,  цикла длины 4, …, 1 цикл длины n. Сумма длин всех фундаментальных циклов будет равна
цикла длины 4, …, 1 цикл длины n. Сумма длин всех фундаментальных циклов будет равна
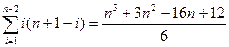 .
.
Таким образом, на некоторых графах число операций этого алгоритма будет величиной порядка 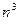 .
.
С пространством циклов тесно связано пространство разрезов графа. Пусть 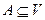 ,
, 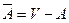 . Разрез графа G, определяемый множеством А, – это остовный подграф, ребрами которого являются все ребра графа, соединяющие вершины из А с вершинами из
. Разрез графа G, определяемый множеством А, – это остовный подграф, ребрами которого являются все ребра графа, соединяющие вершины из А с вершинами из  .
.
Теорема о разрезах. Множество всех разрезов данного графа замкнуто относительно сложения по модулю 2.
Разрез, определяемый одноэлементным множеством А, называется элементарным. Базис пространства разрезов связного графа можно получить, если взять все его элементарные разрезы, кроме одного (любого). Для несвязного графа это нужно проделать для каждой компоненты связности. Таким образом, размерность пространства разрезов графа с k компонентами равна 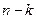 .
.
Пусть 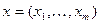 и
и 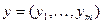 – характеристические векторы двух остовных подграфов графа G. Будем говорить, что эти подграфы ортогональны, если
– характеристические векторы двух остовных подграфов графа G. Будем говорить, что эти подграфы ортогональны, если 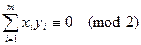 . Это равносильно тому, что подграфы имеют четное число общих ребер.
. Это равносильно тому, что подграфы имеют четное число общих ребер.
Теорема о циклах и разрезах. Любой цикл данного графа ортогонален любому его разрезу.
Так как сумма размерностей пространств циклов и разрезов равна размерности пространства подграфов, то из этой теоремы следует, что пространства циклов и разрезов являются ортогональными дополнениями друг друга. Это можно использовать для построения базиса циклов по матрице инцидентности. Продемонстрируем это на примере. Пусть требуется найти базис циклов для графа, показанного на рисунке 8. Построим его
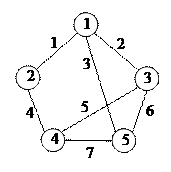
Рис. 8
матрицу инцидентности и удалим из нее одну (любую) строчку (в случае несвязного графа удаляется по одной строке из каждой компоненте связности):
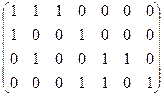
Строки этой матрицы – характеристические векторы элементарных разрезов, образующих базис разрезов. Так как пространство циклов является ортогональным дополнением пространства разрезов, то остается найти фундаментальную систему решений системы линейных однородных уравнений с этой матрицей (над полем из двух элементов). Для этого с помощью операций над строками преобразуем матрицу так, чтобы в первых столбцах образовалась единичная подматрица:
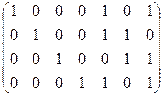
Удаляем первые четыре столбца, оставшуюся матрицу транспонируем и приписываем кт ней справа единичную подматрицу:
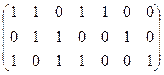
Строки полученной матрицы представляют базис циклов.
 2014-02-04
2014-02-04 2770
2770








