Другой алгоритм для задачи об оптимальном каркасе известен как алгоритм Краскала (J. Kruskal). В нем тоже на каждом шаге рассматривается частичное решение. Отличие от алгоритма Прима состоит в том, что в алгоритме Краскала частичное решение всегда представляет собой остовный лес F графа G, т.е. лес, состоящий из всех вершин графа G и некоторых его ребер. Вначале F не содержит ни одного ребра, т.е. состоит из изолированных вершин. Затем к нему последовательно добавляются ребра, пока не будет построен каркас графа G. Пусть F – лес, построенный к очередному шагу. Новое ребро можно добавить к этому лесу так, чтобы он остался лесом, только если оно соединяет вершины из разных компонент связности леса F. Теперь именно такие ребрабудем называтьподходящими. Для выбора добавляемого ребра применяется тот же принцип, что и в алгоритме Прима – из всех подходящих ребер выбирается ребро наименьшего веса. Для того чтобы облегчить поиск этого ребра, вначале все ребра графа упорядочиваются по возрастанию весов: 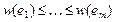 . Теперь последовательность ребер
. Теперь последовательность ребер 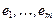 достаточно просмотреть один раз и для очередного рассматриваемого ребра нужно определить, является ли оно подходящим относительно построенного к этому моменту леса F. Подходящие ребра добавляются к F, остальные просто пропускаются.
достаточно просмотреть один раз и для очередного рассматриваемого ребра нужно определить, является ли оно подходящим относительно построенного к этому моменту леса F. Подходящие ребра добавляются к F, остальные просто пропускаются.
Теорема об алгоритме Краскала. Лес F, построенный с помощью алгоритма Краскала, является каркасом наименьшего веса для данного графа.
Скорость работы алгоритма Краскала зависит от того, как организовано хранение информации о текущем лесе и как выполняется проверка подходящих ребер. Применение специальных структур данных, которые мы не будем здесь рассматривать, позволяет реализовать этот алгоритм с оценкой времени работы 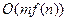 , где
, где 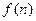 – очень медленно растущая функция. В частности,
– очень медленно растущая функция. В частности, 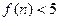 для
для 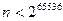 .
.
 2014-02-04
2014-02-04 1341
1341
