Алгоритм Прима

1 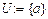, где a – произвольная вершина графа;

2 ;

3 while 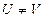do

4 найти ребро наименьшего веса 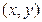среди всех ребер, у которых , ;

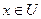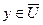5 добавить к F ребро 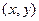, а к U вершину y.

Теорема об алгоритме Прима. Подграф , построенный с помощью алгоритма Прима, является каркасом наименьшего веса для данного графа.

Оценим время работы алгоритма Прима. Цикл while в строке 3 повторяется 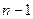раз. Внутри этого цикла есть еще скрытый цикл в строке 4, где ищется ребро наименьшего веса среди подходящих ребер. Допустим, что этот поиск производится самым бесхитростным образом, т.е. просматриваются все пары вершин 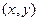с 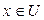, 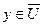. Если , то имеется 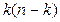таких пар. Всего получаем

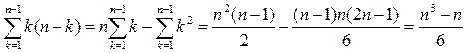
пар, которые нужно рассмотреть. Таким образом, трудоемкость алгоритма будет .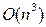

Небольшое усовершенствование позволяет на порядок ускорить этот алгоритм. Допустим, что для каждой вершины y из множества 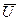известна такая вершина 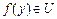, что ребро имеет наименьший вес среди всех ребер вида 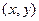, где 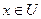. Тогда при 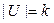для поиска подходящего ребра наименьшего веса достаточно будет сравнить 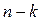ребер вида , а общее число анализируемых ребер будет равно

.

В этом случае, однако, необходимы дополнительные действия для обновления таблицы значений функции f при добавлении новой вершины к дереву, т.е. при переносе одной вершины из множества 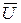в множество U. Сначала, когда множество U состоит из единственной вершины a, полагаем 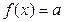для всех 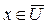. В дальнейшем эти значения могут меняться. Допустим, на некотором шаге к дереву присоединяется вершина y. Тогда для каждой вершины 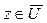либо сохраняется старое значение 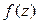, либо устанавливается новое 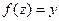, в зависимости от того, какое из ребер 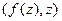и 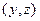имеет меньший вес. По окончании работы алгоритма массив f будет массивом отцов построенного дерева относительно корня а. Поэтому отпадает необходимость отдельно запоминать добавляемые к дереву ребра. Алгоритм теперь можно записать следующим образом.