Вариант 4
Задачи
Потоки
Задачи
Алгоритм Дейкстры.
7 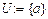 ;
; 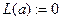 ;
;
8 for 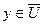 do {
do {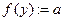 ;
; 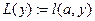 };
};
9 while 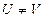 do
do
10 найти вершину 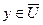 с наименьшим значением
с наименьшим значением 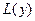 ;
;
11 добавить к U вершину y;
12 for 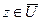 do if
do if 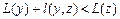 then {
then {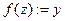 ;
; 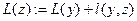 }.
}.
9.1. Найдите оптимальный каркас по матрице весов ребер с помощью алгоритма Прима
(прочерк означает отсутствие ребра).
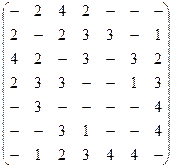

9.2. Найдите оптимальный каркас с помощью алгоритма Краскала.
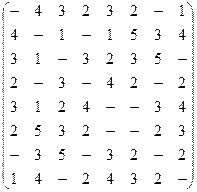
9.3. Какие из следующих утверждений верны для любого взвешенного графа?
1) Если в графе имеется единственное ребро наименьшего веса, то оно принадлежит каждому оптимальному каркасу.
2) Если в графе имеются точно два ребра наименьшего веса, то они оба принадлежат каждому оптимальному каркасу.
3) Если в графе имеются точно три ребра наименьшего веса, то все они принадлежат каждому оптимальному каркасу.
4) Каждое ребро минимального веса принадлежит какому-нибудь оптимальному каркасу.
9.4. Вершины полного графа 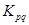 размещаются в в целочисленных точках
размещаются в в целочисленных точках
прямоугольника 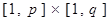 . Вес каждого ребра равен евклидовой длине
. Вес каждого ребра равен евклидовой длине
отрезка, соединяющего вершины этого ребра.
1) Чему равен вес оптимального каркаса для этого графа?
2) Каков будет вес оптимального каркаса, если из графа удалить все ребра длины 1?
3) Каков будет вес оптимального каркаса, если из графа удалить все ребра с длинами
1, 2 и 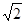 , а
, а 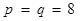 ?
?
4) Каков будет вес оптимального каркаса, если из графа удалить все ребра с длинами
1 и 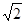 , а
, а 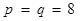 ?
?
9.5. По матрице длин ребер графа с помощью алгоритма Дейкстры найдите
1) кратчайшие пути от вершины 7 до всех остальных вершин
2) кратчайший путь между вершинами 1 и 4;
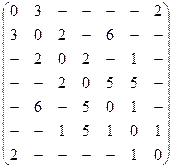
В этом разделе будем рассматривать ориентированные графы без петель и кратных ребер. Для вершины x множество всех входящих в нее ребер обозначается через 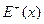 , а множество выходящих – через
, а множество выходящих – через 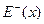 . Сетью называется орграф, в котором
. Сетью называется орграф, в котором
1) каждому ребру e приписано положительное число 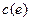 , называемое пропускной способностью ребра;
, называемое пропускной способностью ребра;
2) выделены две вершины s и t, называемые соответственно источником и стоком, при этом 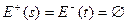 .
.
Вершины сети, отличные от источника и стока, будем называть внутренними.
Пусть задана сеть N с множеством вершин V и множеством ребер Е. Пусть f –функцияс вещественными значениями, определенная на множестве Е. Для вершины х обозначим 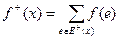 ,
, 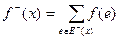 . Функция f называется потоком в сети N, если она удовлетворяет условиям:
. Функция f называется потоком в сети N, если она удовлетворяет условиям:
(1) 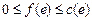 для каждого ребра e;
для каждого ребра e;
(2) 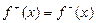 для каждой внутренней вершины x.
для каждой внутренней вершины x.
На рисунке 11 показан пример сети и потока в ней. В дроби, приписанной каждому ребру, числитель представляет пропускную способность ребра, а знаменатель – величину потока на этом ребре.
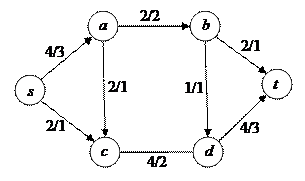
Рис. 11.
Условие (2) называется условием сохранения потока. Так как каждое ребро является входящим для одной вершины и выходящим для другой, то
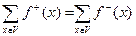 .
.
Из этого равенства и условия сохранения потока следует, что
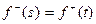 .
.
Эта величина обозначается через  и называется величиной потока. В примере на рисунке
и называется величиной потока. В примере на рисунке 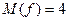 . Задача о максимальном потоке состоит в том, чтобы для данной сети найти поток наибольшей величины.
. Задача о максимальном потоке состоит в том, чтобы для данной сети найти поток наибольшей величины.
Поток на рисунке 11 не является максимальным – можно, например, добавить по единице на ребрах пути 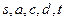 . Получится поток величины 5, показанный на рисунке 12 слева. Но и он не максимален. Можно увеличить поток на 1 на ребрах
. Получится поток величины 5, показанный на рисунке 12 слева. Но и он не максимален. Можно увеличить поток на 1 на ребрах 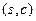 ,
, 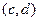 ,
, 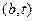 и уменьшить на 1 на ребре
и уменьшить на 1 на ребре 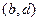 . Условие сохранения останется выполненным, а величина потока станет равной 6 (рисунок 12, справа).
. Условие сохранения останется выполненным, а величина потока станет равной 6 (рисунок 12, справа).
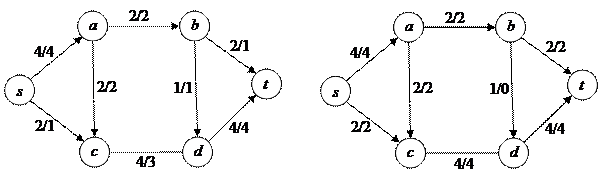
Рис. 12.
Приведенный пример иллюстрирует общий метод, на котором основаны многие алгоритмы решения задачи о максимальном потоке – метод увеличивающих путей. Он является обобщением метода увеличивающих путей для задачи о паросочетании.
Допустим, имеется сеть N и в ней поток f. Пусть 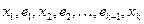 – неориентированный путь в сети. Ребро
– неориентированный путь в сети. Ребро 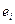 назовем прямым ребром этого пути, если
назовем прямым ребром этого пути, если 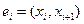 , и обратным, если
, и обратным, если 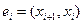 . Путь назовем подходящим относительно потока f, если для каждого прямого ребра выполняется неравенство
. Путь назовем подходящим относительно потока f, если для каждого прямого ребра выполняется неравенство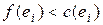 , а для каждого обратного – неравенство
, а для каждого обратного – неравенство 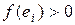 . Таким образом, на каждом прямом ребре подходящего пути поток можно увеличить, а на каждом обратном – уменьшить. Увеличивающий путь – это подходящий путь из источника в сток.
. Таким образом, на каждом прямом ребре подходящего пути поток можно увеличить, а на каждом обратном – уменьшить. Увеличивающий путь – это подходящий путь из источника в сток.
Если имеется увеличивающий путь для потока f, то поток можно увеличить на величину 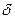 , равную минимуму из величин «недогрузок» (разностей
, равную минимуму из величин «недогрузок» (разностей 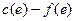 ) прямых ребер этого пути и величин потока на обратных ребрах. Нужно прибавить
) прямых ребер этого пути и величин потока на обратных ребрах. Нужно прибавить 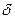 к потоку на каждом прямом ребре пути и вычесть
к потоку на каждом прямом ребре пути и вычесть 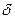 из потока на каждом обратном ребре. Условие сохранения останется выполненным, а величина потока увеличится на
из потока на каждом обратном ребре. Условие сохранения останется выполненным, а величина потока увеличится на 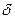 .
.
Теорема об увеличивающем пути. Поток максимален тогда и только тогда, когда относительно него нет увеличивающего пути.
Пусть 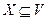 ,
,  , причем
, причем 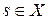 ,
, 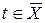 . Множество всех ребер, у которых начальная вершина принадлежит X, а концевая –
. Множество всех ребер, у которых начальная вершина принадлежит X, а концевая – 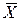 , называется разрезом сети. Пропускная способность разреза есть сумма пропускных способностей его ребер.
, называется разрезом сети. Пропускная способность разреза есть сумма пропускных способностей его ребер.
Теорема о максимальном потоке и минимальном разрезе. Максимальная величина потока равна минимальной пропускной способности разреза данной сети.
Многие известные алгоритмы построения максимального потока основаны на теореме об увеличивающем пути и различаются, в частности, стратегией поиска увеличивающих путей. Первый алгоритм, для которого была получена верхняя оценка трудоемкости, предложили Эдмондс и Карп в 1972 г. В этом алгоритме всегда ищется кратчайший (по числу ребер) увеличивающий путь. Удобно этот поиск вести не на исходной сети N, а на остаточной сети R, которая при заданном на сети N потоке f определяется следующим образом. Множество вершин, источник и сток у остаточной сети те же, что у исходной. Пусть e – ребро исходной сети. Тогда
1) если 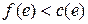 , то ребро e включается в сеть R и ему в этой сети присваивается пропускная способность
, то ребро e включается в сеть R и ему в этой сети присваивается пропускная способность 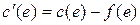 ;
;
2) если 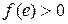 , то к сети R добавляется ребро противоположного направления
, то к сети R добавляется ребро противоположного направления 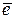 с пропускной способностью
с пропускной способностью 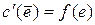 .
.
Легко видеть, что увеличивающие пути в исходной сети находятся во взаимно однозначном соответствии с ориентированными путями из источника в сток в остаточной сети. В алгоритме Эдмондса-Карпа нужно в остаточной сети искать кратчайший ориентированный путь из s в t. Это можно сделать за линейное время с помощью поиска в ширину. Если увеличивающий путь обнаружен, поток увеличивается. Для нового потока строится остаточная сеть и т.д., пока не будет построен поток, относительно которого нет увеличивающего пути (в остаточной сети нет ориентированного пути из источника в сток. Общая оценка трудоемкости алгоритма Эдмондса-Карпа 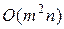 . В настоящее время известны и более быстрые алгоритмы для задачи о максимальном потоке.
. В настоящее время известны и более быстрые алгоритмы для задачи о максимальном потоке.
10.1. Найдите максимальные потоки в изображенных на рисунке сетях.
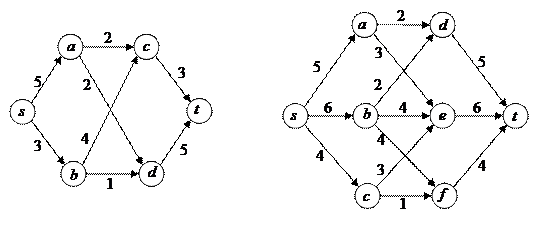
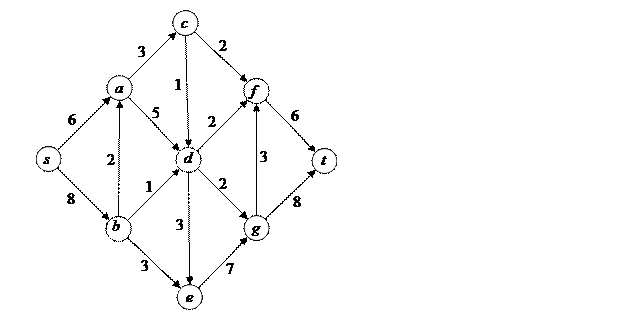
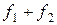 .
.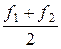 .
.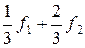 .
.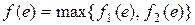 для каждого ребра
для каждого ребра 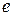 .
.
 2014-02-04
2014-02-04 818
818








