Рассмотрим цепь с двумя параллельными ветвями на рис. 3.22.
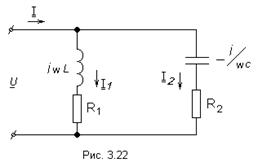
Такую цепь часто называют параллельным контуром. Условием возникновения резонанса является равенство реактивных проводимостей:
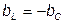 , (3.57)
, (3.57)
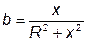 . (3.58)
. (3.58)
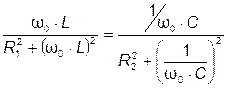 . (3.59)
. (3.59)
При 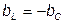 противоположные по фазе реактивные составляющие токов равны, поэтому резонанс в рассматриваемой цепи получил название резонанса токов.
противоположные по фазе реактивные составляющие токов равны, поэтому резонанс в рассматриваемой цепи получил название резонанса токов.
Из векторной диаграммы на рис. 3.23а видно, что при резонансе ток на выходных выводах контура может быть значительно меньше токов в отдельных ветвях.
При резонансе общий ток в параллельном контуре по фазе совпадает с приложенным напряжением.
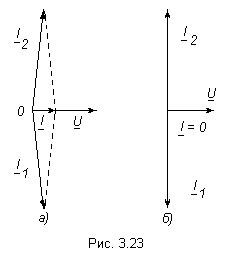
Добротность контура показывает во сколько раз ток в ветви превышает питающий ток и определяется следующим соотношением:
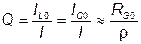 , (3.60)
, (3.60)
где 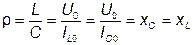 ,
,
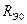 - эквивалентное активное сопротивление при резонансе:
- эквивалентное активное сопротивление при резонансе:
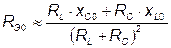 - если
- если 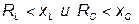 . (3.61)
. (3.61)
В общем случае резонансная частота 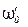 определяется по формуле:
определяется по формуле:
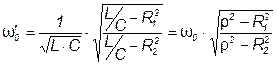 , (3.62)
, (3.62)
где  - резонансная угловая частота при
- резонансная угловая частота при 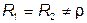 - аналогичная последовательному контуру.
- аналогичная последовательному контуру.
В теоретическом случае при 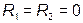 токи
токи  и
и 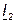 сдвинуты по фазе относительно напряжения на углы
сдвинуты по фазе относительно напряжения на углы 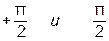 (рис. 3.23б) и суммарный ток
(рис. 3.23б) и суммарный ток 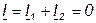 . Входное сопротивление цепи при этом бесконечно велико.
. Входное сопротивление цепи при этом бесконечно велико. 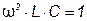
Как видно из формулы 3.62 резонанс возможен, если сопротивления 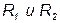 оба больше или оба меньше ρ.
оба больше или оба меньше ρ.
Если 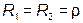 , то резонансная частота
, то резонансная частота 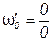 имеет любое значение, то есть резонанс наблюдается на любой частоте.
имеет любое значение, то есть резонанс наблюдается на любой частоте.
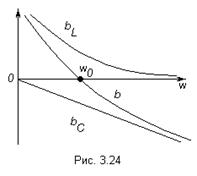 На рис. 3.24 показаны частотные характеристики проводимостей ветвей
На рис. 3.24 показаны частотные характеристики проводимостей ветвей 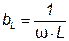 и
и 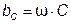 , и входной проводимости цепи
, и входной проводимости цепи 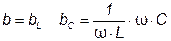 .
.
При изменении частоты от 0 до  эквивалентная проводимость
эквивалентная проводимость 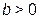 , то есть индуктивная и изменяется от
, то есть индуктивная и изменяется от 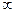 до 0. При
до 0. При 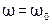 наступает резонанс токов,
наступает резонанс токов, 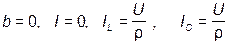 .
.
При возрастании частоты от 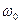 до
до 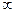 входная проводимость
входная проводимость 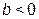 , то есть имеет емкостной характер и изменяется от 0 до
, то есть имеет емкостной характер и изменяется от 0 до 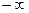 .
.
 2014-02-04
2014-02-04 716
716








