Активное сопротивление
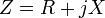 , где
, где 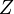 — импеданс,
— импеданс, 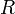 — величина активного сопротивления,
— величина активного сопротивления, 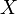 — величина реактивного сопротивления,
— величина реактивного сопротивления, 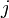 — мнимая единица.
— мнимая единица.
Активное сопротивление — сопротивление электрической цепи или её участка, обусловленное необратимыми превращениями электрической энергии в другие виды энергии (в тепловую).
Реактивное сопротивление
Реактивное сопротивление — электрическое сопротивление, обусловленное передачей энергии переменным током электрическому илимагнитному полю (и обратно).
Реактивное сопротивление определяет мнимую часть импеданса:
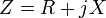 , где
, где 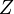 — импеданс,
— импеданс, 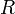 — величина активного сопротивления,
— величина активного сопротивления, 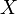 — величина реактивного сопротивления,
— величина реактивного сопротивления, 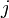 — мнимая единица.
— мнимая единица.
В зависимости от знака величины 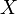 какого-либо элемента электрической цепи говорят о трёх случаях:
какого-либо элемента электрической цепи говорят о трёх случаях:
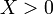 — элемент проявляет свойства индуктивности.
— элемент проявляет свойства индуктивности.
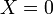 — элемент имеет чисто активное сопротивление.
— элемент имеет чисто активное сопротивление.
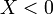 — элемент проявляет ёмкостные свойства.
— элемент проявляет ёмкостные свойства.
Величина реактивного сопротивления может быть выражена через величины индуктивного и ёмкостного сопротивлений:
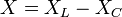
Индуктивное сопротивление (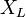 ) обусловлено возникновением ЭДС самоиндукции в элементе электрической цепи. Изменение тока и, как следствие, изменение его магнитного поля вызывает препятствующее изменению этого тока ЭДС самоиндукции. Величина индуктивного сопротивления зависит от индуктивности
) обусловлено возникновением ЭДС самоиндукции в элементе электрической цепи. Изменение тока и, как следствие, изменение его магнитного поля вызывает препятствующее изменению этого тока ЭДС самоиндукции. Величина индуктивного сопротивления зависит от индуктивности 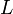 элемента и частоты
элемента и частоты 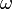 протекающего тока:
протекающего тока:
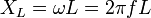
Ёмкостное сопротивление (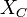 ). Величина ёмкостного сопротивления зависит от ёмкости элемента
). Величина ёмкостного сопротивления зависит от ёмкости элемента 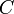 и также частоты протекающего тока
и также частоты протекающего тока 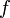 :
:
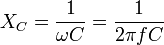
Здесь 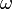 — циклическая частота, равная
— циклическая частота, равная 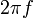 .
.
Прямая и обратная зависимость этих сопротивлений от частоты тока 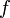 приводит к тому, что с увеличением частоты всё бо?льшую роль начинает играть индуктивное сопротивление и всё меньшую ёмкостное.
приводит к тому, что с увеличением частоты всё бо?льшую роль начинает играть индуктивное сопротивление и всё меньшую ёмкостное.
Полное сопротивление
Полное сопротивление (z) - это векторная сумма всех сопротивлений: активного, емкостного и индуктивного.
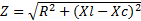
Треугольники сопротивлений
Если стороны треугольника напряжений (155, а) разделить на ток I (.155, б), то углы треугольника от этого не изменятся, и мы получим новый треугольник, подобный первому — треугольник сопротивлений (155, в).
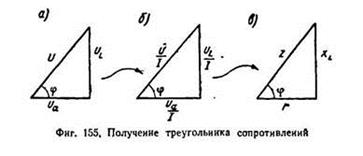 |
В треугольнике сопротивления, показанном на рис, все стороны обозначают сопротивления, причем гипотенуза его является полным или кажущимся сопротивлением цепи.
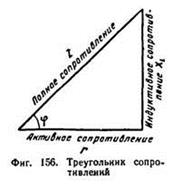 |
Из треугольника сопротивлений видно, что полное или кажущееся сопротивление Z равно геометрической сумме активного R и индуктивного Xl сопротивлений.
Применяя теорему Пифагора к треугольнику сопротивлений, получаем:
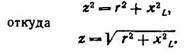 |
 2015-05-13
2015-05-13 33938
33938
