Часто для упрощения расчетов часть схемы заменяют эквивалентной схемой без индуктивных связей. Такой приём ещё называют развязкой индуктивных связей.
Рассмотрим эквивалентную замену для схемы, приведённой на (рис. 4.8). Здесь токи 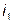 и
и 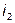 одинаково ориентированы относительно одноимённых зажимов, поэтому включение катушек согласное.
одинаково ориентированы относительно одноимённых зажимов, поэтому включение катушек согласное.
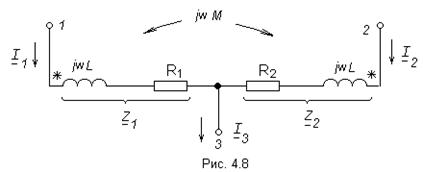
Запишем выражение для напряжений между выводами 1,3 и 2,3:
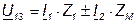 ; (4.20)
; (4.20)
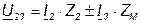 . (4.21)
. (4.21)
Верхние точки «+» относятся к согласному включению катушек, а нижние - к встречному. Далее этот порядок будет сохраняться.
Согласно первому закону Кирхгофа имеем:
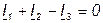 . (4.22)
. (4.22)
Выразив из этого равенства токи 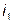 и
и 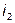 и подставив их, соответственно, во: второе и первое уравнения (4.20 и 4.21), получим:
и подставив их, соответственно, во: второе и первое уравнения (4.20 и 4.21), получим:
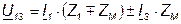 ;
;
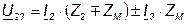 .
.
Причем:
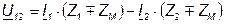 .
.
Эти уравнения справедливы для схемы показанной на (рис. 4.9а,б), которая и является искомой эквивалентной схемой без индуктивных связей.
 Таким образом, при устранении индуктивной связи к сопротивлениям
Таким образом, при устранении индуктивной связи к сопротивлениям 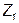 и
и 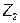 добавляется
добавляется 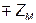 (
(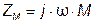 , верхний знак «-» - при согласном включении, нижний знак «+» - при встречном включении катушек), а между узлами
, верхний знак «-» - при согласном включении, нижний знак «+» - при встречном включении катушек), а между узлами 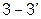 появляется элемент
появляется элемент 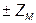 .
.
|
|
|
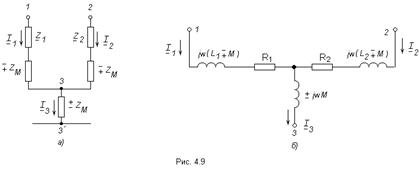
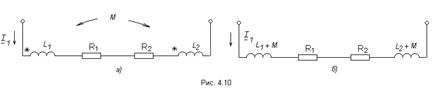
Если две индуктивно связанные катушки соединены последовательно (рис. 4.10а), то при замене на эквивалентную схему без индуктивной связи получается схема, показанная на (рис. 4.10б).
В данном случае катушки соединены согласно.
 |  | ||
4.5 Трансформатор. Вносимое сопротивление. Векторная диаграмма
Трансформатор - это устройство с двумя или более обмотками для преобразования напряжения. Обмотка, присоединённая к источнику называется первичной, соединённая с нагрузкой - вторичная.
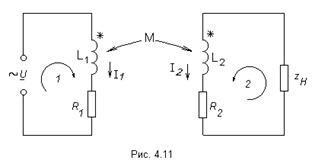
На (рис. 4.11) изображена схема для магнитно-связанных катушек в режиме трансформатора.
Для этой схемы по второму закону Кирхгофа для первичного и вторичного контуров можно записать:
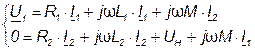 (4.23)
(4.23)
где 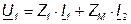
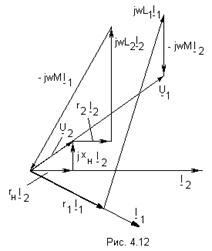
Построим векторную диаграмму для первичной и вторичной цепей. Зададим для этого вектор тока 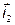 . Отложим векторы
. Отложим векторы 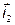 ,
,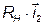 ,
, 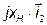 ,
, 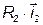 и
и 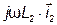 (рис 4.12), причем примем
(рис 4.12), причем примем 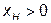 , то есть
, то есть  (рис. 4.12). Соединив конец вектора
(рис. 4.12). Соединив конец вектора 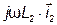 с началом векторной диаграммы, получим, как следует из второго уравнения 4.23, вектор
с началом векторной диаграммы, получим, как следует из второго уравнения 4.23, вектор 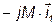 . Разделив напряжение
. Разделив напряжение 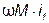 на
на 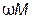 , определим значение тока
, определим значение тока 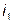 . Вектор
. Вектор 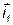 отложим под углом
отложим под углом 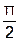 (в сторону опережения) к вектору
(в сторону опережения) к вектору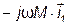 . Затем построим векторы
. Затем построим векторы 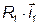 ,
, 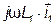 и
и
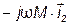 .
.
 |
Решив уравнения 4.23 относительно тока
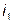 , получим:
, получим: 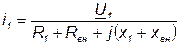 ,
,
где 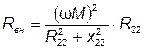 ;
;
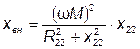 ;
;
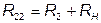 ;
;
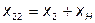 .
.
 Сопротивления
Сопротивления 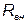 и
и 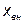 называют вносимыми (из второго контура в первый) активными и реактивными сопротивлениями.
называют вносимыми (из второго контура в первый) активными и реактивными сопротивлениями.
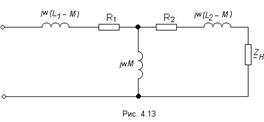
С помощью эквивалентной замены индуктивно связанных катушек цепь на (рис. 4.11) можно представит в виде цепи, изображенной на (рис. 4.13).
Если при любых сопротивлениях нагрузки отношение первичного и вторичного комплексных токов равны друг другу и равны постоянному действительному числу, то есть трансформатор называется идеальным.
|
|
|
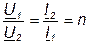 . (4.24)
. (4.24)
Число n называется коэффициентом трансформации идеального трансформатора.
Найдём входное сопротивление со стороны первичных выводов:
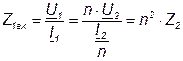 . (4.25)
. (4.25)
То есть оно в 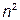 раз больше сопротивления
раз больше сопротивления 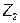 . Аналогичным путём можно показать, что
. Аналогичным путём можно показать, что
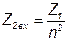 . (4.26)
. (4.26)
Эти отношения характеризуют трансформацию сопротивлений. Если вторичные выводы разомкнуты, то 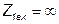 , если они замкнуты, то
, если они замкнуты, то 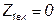 .
.
Если коэффициент трансформации 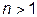 , то трансформатор повышающий,
, то трансформатор повышающий, 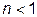 - понижающий.
- понижающий.
ГЛАВА 5 РАСЧЁТ ТРЁХФАЗНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
 2014-02-04
2014-02-04 3050
3050