Рисунок 14.5
Рисунок 14.4
Рисунок 14.3
Рисунок 14.2
Рисунок 14.1
На рис.14.1в приведено вариант схемы, в которой одна ветка содержит тольки индуктивность 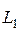 , а другая - индуктивность
, а другая - индуктивность 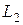 и емкость C. Такую схему называют контуром второго вида или контуром с распределенной индуктивностью. В контуре третьего вида (с распределенной емкостью) (рис.14.1г) к одной ветке подключена тольки емкость
и емкость C. Такую схему называют контуром второго вида или контуром с распределенной индуктивностью. В контуре третьего вида (с распределенной емкостью) (рис.14.1г) к одной ветке подключена тольки емкость 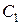 , а к другой - емкость
, а к другой - емкость 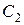 и индуктивность L. Контуры второго и третьего видов носят название также сложных или контурами с частичным включением.
и индуктивность L. Контуры второго и третьего видов носят название также сложных или контурами с частичным включением.
Найдем входное (эквивалентное) сопротивление сложного контура
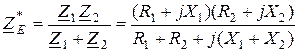 .
.
Для контуров с высокой добротностью 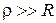 . Тогда
. Тогда
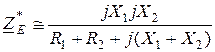 .
.
Вычислим эквивалентное резонансное сопротивление. Поскольку при 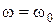 выполняется условие (14.1), будем иметь
выполняется условие (14.1), будем иметь
 ,
,
где 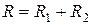 - активное сопротивление параллельного контура при последовательном обходе;
- активное сопротивление параллельного контура при последовательном обходе; 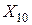 - реактивное сопротивление ветки, которая содержит реактивность одного характера.
- реактивное сопротивление ветки, которая содержит реактивность одного характера.
Обозначим величину 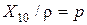 - коэффициент включения и запишем выражение для эквивалентного резонансного сопротивления сложного контура:
- коэффициент включения и запишем выражение для эквивалентного резонансного сопротивления сложного контура:
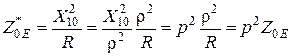 . (14.2)
. (14.2)
Найдем формулы для расчета резонансной частоты и коэффициента включения для контуров второго и третьего видов.
1. Контур II вида. Резонансная частота определяется из формулы (14.1):
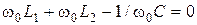 , откуда имеем
, откуда имеем
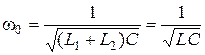 , (14.3)
, (14.3)
где 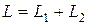 - полная индуктивность контура.
- полная индуктивность контура.
Зная резонансную частоту, находим коэффициент включения:
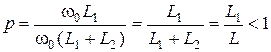 .
.
2. Контур III вида. Формула (14.1) является справедливой и в этом случае:
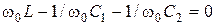 . Итак, резонансная частота будет представляться
. Итак, резонансная частота будет представляться
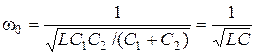 , (14.4)
, (14.4)
где 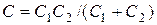 - полная емкость контура.
- полная емкость контура.
Коэффициент включения равняется:
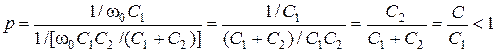 .
.
Поскольку коэффициент включения меньше единицы, делаем вывод, что частичное включение позволяет в 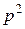 раз уменьшить резонансное сопротивление параллельного контура по сравнению с полным включением.
раз уменьшить резонансное сопротивление параллельного контура по сравнению с полным включением.
14.1 Частотные характеристики полного сопротивления сложных
параллельных контуров
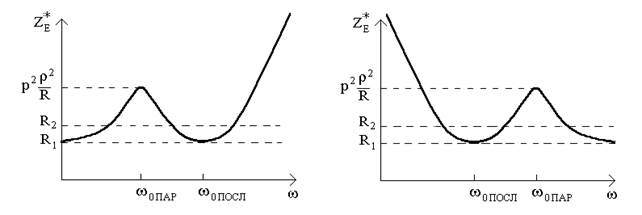
Характерной особенностью сложных параллельных контуров является то, что с резонансом токов в контуре возможны резонансы напряжений в ветках. Поэтому в отличии от простого контура, частотная зависимость полного сопротивления сложного контура имеет два екстремума (рис.14.2а соответствует контуру второго вида, а рис.14.2б - контуру третьего вида).
а) б)
Для контура II вида частота параллельного резонанса определяется по формуле (14.3): 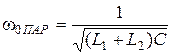 , а частота последовательного резонанса - по формуле
, а частота последовательного резонанса - по формуле 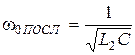 .
.
Из этих соотношений видно, что поскольку 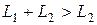 , то
, то 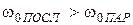 .
.
Для контура III вида по формуле (14.4) находим
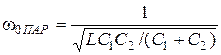 ;
; 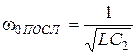
Поскольку 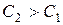 , то
, то 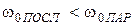 .
.
Вывод. Частотные характеристики сложного контура позволяют использовать его для пропуска сигналов одних частот и послабление сигналов других частот.
14.2 Индуктивно-связанные электрические цепи
Связанные электрические цепи - электрические цепи, процессы в которых влияют друг на друга через совместное магнитное или электрическое поле.
В индуктивно-связанныех электрических цепях процессы влияют друг на друга через совместное магнитное поле.
1. Общие понятия об индуктивно-связанных цепях.
Вопрос относительно магнитного поля катушки и ее индуктивности был рассмотрен в первой лекции. Напомним, что для индуктивной катушки, которая состоит из N витков, потокосцепление (т.е. сумма магнитних потоков, сцепленных с витками элемента электрической цепи) определяется таким способом: 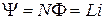 .
.
ЭДС самоиндукции связана с 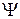 :
: 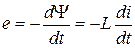 .
.
Рассмотрим две катушки, которые размещены одна около другой (рис.14.3). Возможны два случая:
1) Ток 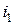 проходит тольки через катушку 1, катушка 2 розомкнута (
проходит тольки через катушку 1, катушка 2 розомкнута ( ). Тогда полный поток самоиндукции будет представлен:
). Тогда полный поток самоиндукции будет представлен:
 ,
,
где 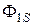 - поток рассеивания (часть потока
- поток рассеивания (часть потока 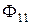 , который не пронизывает витки катушки 2);
, который не пронизывает витки катушки 2); 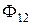 - поток взаимоиндукции (поток тока
- поток взаимоиндукции (поток тока 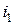 , но сцепленный с витками
, но сцепленный с витками 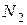 ).
).
Потокосцепление  , ЭДС самоиндукции
, ЭДС самоиндукции  и напряжение
и напряжение 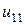 определяются по формулам:
определяются по формулам: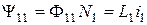 ;
; 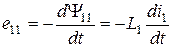 ;
; 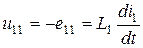 ;
;
2) Токи проходят одновременно через обе катушки (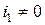 ,
,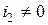 ). В этом случае общий магнитный поток катушки 1 будет равняться:
). В этом случае общий магнитный поток катушки 1 будет равняться:
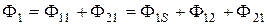 ,
,
где 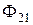 - поток взаимоиндукции тока
- поток взаимоиндукции тока 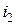 , сцепленный с витками
, сцепленный с витками 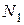 .
.
Полное потокосцепление катушки 1 будет равняться:
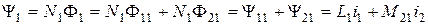 ,
,
где 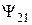 - потокосцепление взаимоиндукции;
- потокосцепление взаимоиндукции; 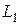 - коэффициент самоиндукции (или индуктивность);
- коэффициент самоиндукции (или индуктивность); 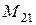 - коэффициент взаимоиндукции (или взаимная индуктивность).
- коэффициент взаимоиндукции (или взаимная индуктивность).
Взаимная индуктивность - отношение значения потокосцепления взаємоиндукции одной электрической цепи к значению тока другой цепи, что определяет это потокосцепление: 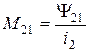 .
.
Аналогично можно записать полное потокосцепление катушки 2:
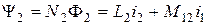 .
.
Поскольку для линейных электрических цепей выполняется равенство 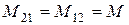 , для суммарных ЭДС и напряжений, которые приводятся на зажимах каждой из катушек, можно записать:
, для суммарных ЭДС и напряжений, которые приводятся на зажимах каждой из катушек, можно записать:
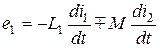 ;
; 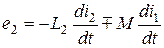 ;
;
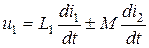 ;
; 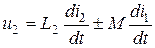 . (14.5)
. (14.5)
Поскольку в общем случае потоки само- и взаимоиндукции могут как суммироваться, так и вычитаться, в формуле указываются знаки "±". Знак зависит от того, каким образом подключены катушки: встречно или согласованно.
2. Одноименные зажимы. Встречное и согласованное включение индуктивно-связанных катушек.
Два зажима, которые принадлежат двум разным, индуктивно-связанным катушкам, носят название одноименных, если при одинаковом направлении токов относительно этих зажимов магнитные потоки само- та взаимоиндукции суммируются.
Согласованным (встречным) называется включение индуктивных катушек, при котором потоки само- и взаимоиндукции суммируются (вычитаются).
На рис.14.4 изображены две катушки, которые размещены близко друг к другу и соединены согласованно. В каждой из этих катушек при смене величины тока индуцируется как ЭДС самоиндукции, так и ЭДС взаимноиндукции. Согласно (14.5) суммарное индуцированное напряжение в каждой котушке определяется по формулам:
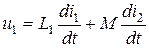 ;
; 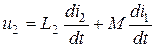 .
.
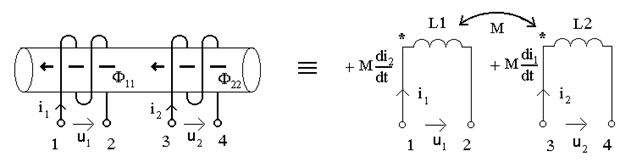
На рис.14.5 две катушки соединенны встречно. Магнитные потоки при токах 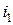 ,
, 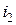 имеют противоположные направления, поэтому и индуцированные в катушках ЭДС и напряжения взаимоиндукции имеют противоположные направления:
имеют противоположные направления, поэтому и индуцированные в катушках ЭДС и напряжения взаимоиндукции имеют противоположные направления:
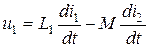 ;
; 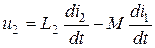 .
.
Замечание. Если в схеме (рис.14.5) сменить направление второго тока на противоположное (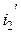 ), то магнитный поток также сменит направление (
), то магнитный поток также сменит направление (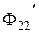 ), и соединение катушек станет согласованным.
), и соединение катушек станет согласованным.
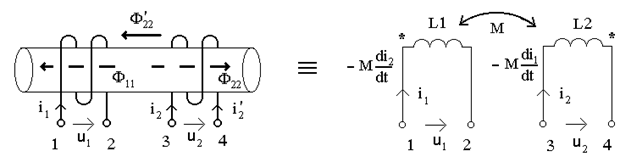
3. Коэффициент связи.
Найдем соотношение между напряжениями 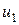 и
и 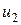 индуктивно-связанных катушек 1 i 2. Рассмотрим три варианта:
индуктивно-связанных катушек 1 i 2. Рассмотрим три варианта:
1) 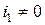 ,
, 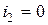 . Тогда
. Тогда 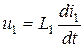 ;
; 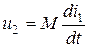 ; коэффициент передачи (или коэффициент степени связи катушки 1 с катушкой 2 будет иметь вид
; коэффициент передачи (или коэффициент степени связи катушки 1 с катушкой 2 будет иметь вид
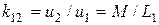 .
.
2) 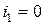 ,
, 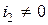 ;
; 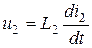 ;
; 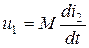 . Тогда
. Тогда 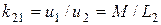 .
.
3) 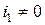 ,
,  . В этом случае будем иметь
. В этом случае будем иметь
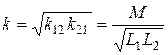 .
.
Итак, коэффициент связи двух катушек - это отношение взаимной индуктивности двух катушек к среднему геометрическому значению собственных индуктивностей.
Коэффициент связи характеризует степень индуктивной связи двух катушек (контуров). Рассматривают три степени связи:
очень слабая связь, k = 0,001...0,01;
слабая связь, k = 0,01...0,1;
сильная связь, k = 0,1...0,9.
Предположим, что к системе двух индуктивно-связанных катушек подводиться синусоидная ЭДС. Тогда в каждой из катушек будут протекать токи: 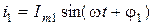 ,
, 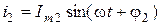 .
.
Согласно формуле (14.5) мгновенное значение напряжения на зажимах первой катушки будет иметь вид:
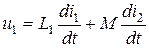 .
.
Переходя к комплексно-временным функциям, будем иметь
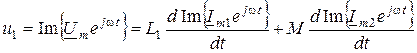 .
.
Учитывая комутативность операции взятия мнимой части, получаем
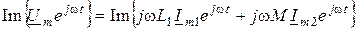 ;
;
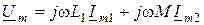 ;
; 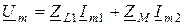 ,
,
где 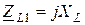 - комплексное сопротивление катушки
- комплексное сопротивление катушки 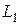 ;
;
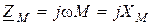 - комплексное сопротивление связи;
- комплексное сопротивление связи; 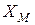 - сопротивление связи.
- сопротивление связи.
С учетом введенных определений коэффициент связи определяется по формуле:
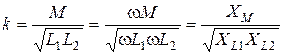 .
.
Рассмотрим последовательное соединение двух индуктивно-связанных катушек, к которым подводиться синусоидное напряжение 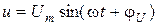 :
:
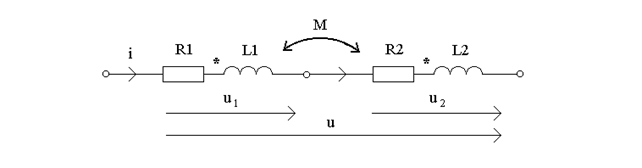
1. Согласованное включение (рис.15.1).
 2014-02-09
2014-02-09 1095
1095








