Относительное удлинение и угол сдвига

Лекция 22 Деформированное состояние

Деформацией называется такое изменение положений точек тела, при котором изменяются расстояния между любыми двумя его точками.

Деформация возникает вследствие нагрузки тела или вследствие изменения температуры. Изменение положений точек тела может привести к изменению длин и к изменению углов в теле. В первом случае возникает линейная деформация, а во втором угловая деформация. Линейная деформация измеряется относительным удлинением, а угловая деформация – углом сдвига.

Относительное удлинение.

Рассмотрим стержень, на котором сделаны две отметки на расстоянии 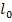друг от друга. Приложим к стержню растягивающую нагрузку (рис.1)

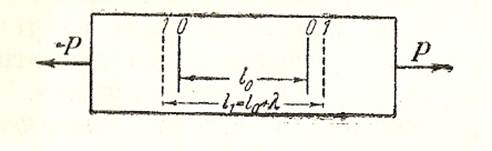
Рис.1.

Расстояние между отметками увеличится и сделается равным

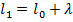
Найдем отношение

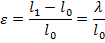
Т.е. отношение изменения длины к первоначальной длине называется относительным удлинением. Относительное удлинение является безразмерной величиной.

Угол сдвига. Плоское напряженное состояние, при котором на двух парах взаимно перпендикулярных плоскостей имеются только касательные напряжения, называется чистым сдвигом. Возьмем частицу в форме прямоугольного параллелепипеда и закрепим неподвижно ее основание (рис.2). Подвергнем параллелепипед чистому сдвигу. Его углы из прямых сделаются косыми.

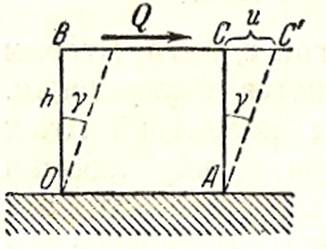Рис.2

Величина 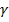, на которую изменился первоначально прямой угол, называется углом сдвига. Так как при малых углах 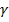можно принять, что 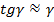, то из рисунка видно, что:

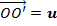будем называть вектором перемещений (перемещением) точки О. Покажем, что шесть компонентов тензора деформации в точке О можно выразить через производные от компонентов u, v, w вектора перемещения точки О по координатам x, y, z. При этом будем предполагать, что перемещение 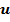и его компоненты u, v, w по направлениям, совпадающим с ребрами параллелепипеда, являются непрерывными и дифференцируемыми функциями.

Пусть компонент перемещения начальной точки О ребра 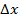в направлении х равен u, тогда компонентом перемещения точки А этого ребра в том же направлении будет: