Матрица перехода от базиса к базису. Преобразование координат вектора при переходе к новому базису.
n – мерное пространство.
Vn – базис, состоящий из n векторов.
В пространстве есть базисы 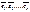 Введем матрицу перехода от
Введем матрицу перехода от 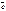 к
к  .
.
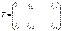
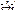
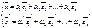
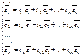
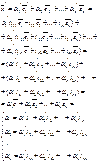
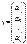
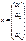
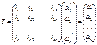
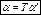
Рассмотрим линейное пространство V, в котором уже есть 2 операции (сложение и умножение). В этом пространстве введем еще одну операцию. Она будет удовлетворять следующим аксиомам.
1. 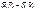
2. 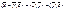
3. 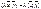
4. 
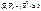
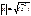 Указанная операция называется скалярным произведением векторов. N – мерное линейное пространство с введенной операцией скалярного произведения, называется Евклидовым пространством.
Указанная операция называется скалярным произведением векторов. N – мерное линейное пространство с введенной операцией скалярного произведения, называется Евклидовым пространством.
Длиной вектора называется арифметическое значение квадратного корня и скалярного квадрата.
Длина вектора удовлетворяет следующим условиям:
1. 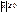 , если
, если 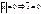
2. 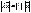
3. 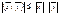 - неравенство Коши-Буня
- неравенство Коши-Буня
4. 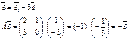
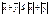 - неравенство треугольника
- неравенство треугольника
13.Скалярное произведение векторов и его свойства.
 Скалярным произведением двух ненулевых векторов называется число, равное произведению этих векторов на косинус угла между ними.
Скалярным произведением двух ненулевых векторов называется число, равное произведению этих векторов на косинус угла между ними.
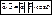
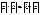
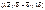
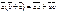
 2014-02-04
2014-02-04 525
525








