Собственные векторы линейного оператора и их свойства.
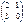 Ненулевой вектор
Ненулевой вектор 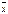 называется собственным вектором линейного оператора, если
называется собственным вектором линейного оператора, если 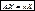 оператор к
оператор к 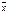 , получим этот же
, получим этот же  , умноженный на некоторое к.
, умноженный на некоторое к.
к – собственное число оператора А=
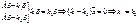 Каждый собственный вектор имеет единственное собственное число.
Каждый собственный вектор имеет единственное собственное число.
Векторное уравнение прямой.
Положение прямой можно задать по точке и направляющему вектору.
Пусть прямая L задана ее точкой M0(x0;y0;z0) и направляющим вектором S(m;n;p). Возьмем на прямой L точку M(x;y;z). Обозначим радиус-векторы точек M и M0 через r и r0.
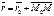
Тогда уравнение прямой запишется в виде: 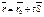
где t – скалярный множитель (параметр).
Параметрические уравнения прямой.
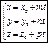
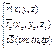
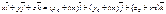
Канонические уравнения прямой.
S(m;n;p) – направляющий вектор прямой L. M0(x0;y0;z0) – точка на прямой. 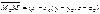 соединяет M0 с произвольной точкой М.
соединяет M0 с произвольной точкой М.
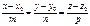
Уравнение прямой в пространстве, проходящей через две точки.
M1(x1;y1;z1) M2(x2;y2;z2)
 В качестве направляющего вектора можно задать вектор
В качестве направляющего вектора можно задать вектор 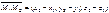
Следовательно:
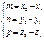 ,тогда
,тогда 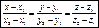
Общее уравнение прямой.
Уравнение прямой как линию пересечения двух плоскостей. Рассмотрим:
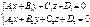
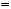
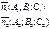
Т.к. прямая перпендикулярна векторам n1 и n2 то направляющий вектор запишется как векторное произведение:
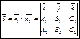
 2014-02-04
2014-02-04 296
296








