2014-02-02
269
Если Х является не непрерывной случайной величиной, а дискретной случайной величиной, то при большом числе значений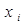 
(когда N>100, Онадзани стр. 393) параметры m и 
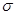рассчитываются по формулам:
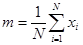
N-образцов, 
- математической ожидание для совокупности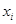 
образцов
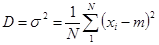
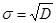
У 99,7% из общего N числа случайных величин значения указываются в интервале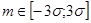 
.
При небольшом (???) n числе случайных величин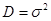 
и стандартное.
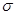- отклонение рассчитывается по формуле
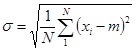(1)
Параметр 
представляет собой уменьшение на единицу число случайных величин называется числом степеней свободы.
Вернёмся к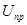 
и 
. Для них функция распределения и плотность вероятности их значений, соответствующая нормальному закону смотрятся
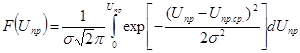- вероятность существования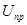
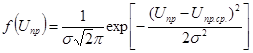- плотность вероятности
Значения таких параметров, как 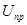или , добываемые на практике не являются случайными величинами, а являются дискретными. В таком случае параметры, определяющие вид таких функций: 
и 
определяют по формулам (1).
Отметим, что случайный процесс обладает нормальным распределение, если он может быть представлен суммой большого числа произв. образом распределённых случайных величин. Каждая из которых привносит незначительный вклад в общую сумму (например пробой воздушного промежутка).
