1. Выбирают положительное направление тока IН в ветви с нагрузкой.
2.Удаляют сопротивление нагрузки 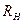 и в месте разрыва изображают стрелку, направленную так же, как ток
и в месте разрыва изображают стрелку, направленную так же, как ток 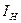 в ветви нагрузки. Стрелка указывает направление напряжения холостого хода
в ветви нагрузки. Стрелка указывает направление напряжения холостого хода 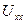 .
.
3. Находят величину 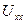 :
:
- записывают уравнение по второму закону Кирхгофа для фиктивного контура, включающего 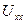 и не вносящего дополнительных неизвестных UJ;
и не вносящего дополнительных неизвестных UJ;
- в режиме холостого хода рациональным методом находят токи ветвей, входящие в уравнение для 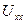 ;
;
- рассчитывают величину 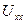 .
.
4. Определяют входное сопротивление RBX относительно точек разрыва. Возможно несколько способов:
а) 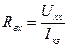 ,
,
где 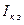 - ток короткого замыкания, направленный также как
- ток короткого замыкания, направленный также как 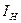 ;
;
б) при отсутствии в схеме управляемых источников расчет входного сопротивления рациональнее всего выполнять сворачиванием схемы к входным зажимам пассивной схемы, полученной из активной схемы, путем замены автономных источников энергии их внутренними сопротивлениями;
в) в схеме с автономными и управляемым источниками энергии автономные источники энергии заменяют их внутренними сопротивлениями. К зажимам полученной схемы подключают пробный источник и рассчитывают неизвестный пробный ток. Получают как
как
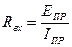
при одинаковом направлении 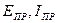 .
.
5. Рассчитывают ток через сопротивление нагрузки
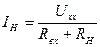 .
.
Пример: Дано: 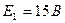 ,
, 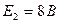 ,
, 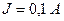 ,
, 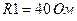 ,
,  ,
, 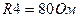 ,
, 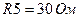 .
.
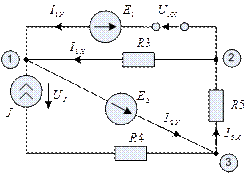
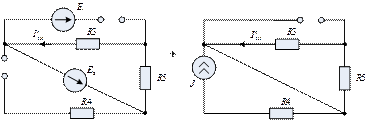
Рис. 2.6.1
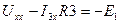 =>
=> 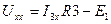
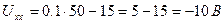 ,
,
где 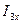 - ток
- ток 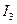 в режиме холостого хода.
в режиме холостого хода. 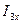 можно найти:
можно найти:
1) из системы уравнений по законам Кирхгофа
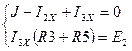
Откуда 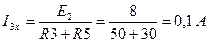 .
.
2) по методу наложения
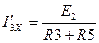 ,
, 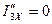 ,
,

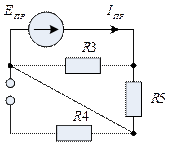
рис. 2.6.2
Согласно рис. 2.6.2:
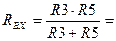
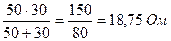 .
.
Тогда: 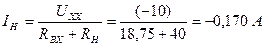 .
.
 2014-02-04
2014-02-04 519
519








