При неустановившемся движении форма и местоположение элементарных струек непрерывно изменяются.
Трубка тока является как бы непроницаемой для частиц жидкости, а элементарная струйка представляет собой элементарный поток жидкости.
Если выделить в движущейся жидкости элементарный замкнутый контур площадью dЙ и через все точки этого контура провести линии тока, то получится трубчатая поверхность, которую называют трубкой тока. Часть потока, ограниченная поверхностью трубки тока, называется элементарной струйкой жидкости. Таким образом, элементарная струйка жидкости заполняет трубку тока и ограничена линиями тока, проходящими через точки выделенного контура с площадью dЙ. Если dЙ устремить к 0, то элементарная струйка превратится в линию тока.
Из приведённых выше определений вытекает, что в любом месте поверхности каждой элементарной струйки (трубки тока) в любой момент времени вектора скоростей направлены по касательной (и, следовательно, нормальные составляющие отсутствуют). Это означает, что ни одна частица жидкости не может проникнуть внутрь струйки или выйти наружу.
При установившемся движении элементарные струйки жидкости обладают рядом свойств:
· площадь поперечного сечения струйки и ее форма с течением времени не изменяются, так как не изменяются линии тока;
· проникновение частиц жидкости через боковую поверхность элементарной струйки не происходит;
· во всех точках поперечного сечения элементарной струйки скорости движения одинаковы вследствие малой площади поперечного сечения;
· форма, площадь поперечного сечения элементарной струйки и скорости в различных поперечных сечениях струйки могут изменяться.
Кроме того, установившееся движение подразделяется на равномерное и неравномерное.
- Часть 1
- | 2
- | 3
 Поток идеальной жидкости, как указывалось ранее, можно представить совокупностью элементарных струек жидкости. Скорости по сечению потока неодинаковы, причём в середине потока скорости наибольшие, а к периферии они уменьшаются (струйная модель потока). Это означает, что различные струйки в одном сечении имеют различные значения кинетической энергии. Отсюда следует, что кинетическая энергия, посчитанная с использованием скоростей элементарных струек uS, и кинетическая энергия, посчитанная с использованием значения средней скорости потока V, будет иметь разные значения. Выясним, какова эта разница. Кинетическая энергия элементарной струйки
Поток идеальной жидкости, как указывалось ранее, можно представить совокупностью элементарных струек жидкости. Скорости по сечению потока неодинаковы, причём в середине потока скорости наибольшие, а к периферии они уменьшаются (струйная модель потока). Это означает, что различные струйки в одном сечении имеют различные значения кинетической энергии. Отсюда следует, что кинетическая энергия, посчитанная с использованием скоростей элементарных струек uS, и кинетическая энергия, посчитанная с использованием значения средней скорости потока V, будет иметь разные значения. Выясним, какова эта разница. Кинетическая энергия элементарной струйки 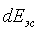 равна:
равна:

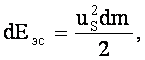
где 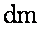 - масса жидкости плотностью
- масса жидкости плотностью  , протекающей через живое сечение элементарной струйки
, протекающей через живое сечение элементарной струйки 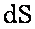 со скоростью
со скоростью 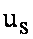 за время dt, равная:
за время dt, равная:
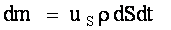 .
.
Проинтегрировав выражение для  , получим выражение для кинетической энергии потока идеальной жидкости
, получим выражение для кинетической энергии потока идеальной жидкости 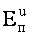 .
.
 2014-02-02
2014-02-02 706
706








