Уравнение Бернулли. Рассмотрим узкую трубку тока и два ее сечения 1 и 2

Рассмотрим узкую трубку тока и два ее сечения 1 и 2. Пусть площади сечений равны S₁ и S₂, а скорости потока в сечениях 1 и 2 равны v₁ и v₂. Рассмотрим очень маленький промежуток времени Δt. За это время жидкость в сечении 1 переместится на расстояние 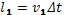, а в сечении 2 на . Рассмотрим объем жидкости, заключенный между сечениями 1 и 2. Если давление жидкости в сечении 1 равно Р₁, а в сечении 2 – Р₂, то за время Δt силы давления совершают над выделенным объемом работу A(силы давления окружающей жидкости на боковую поверхность трубки тока направлены перпендикулярно поверхности трубка, а значит их работа равна нулю). Эта работа равна изменению энергии выделенного объема жидкости. Но за время Δt слой жидкости толщиной v₁Δt между штриховыми линиями в сечении 1 переместился в слой толщиной v₂Δt в сечении 2. Значит, совершенная силами давления работа равна разности энергий этих двух слоев жидкости:

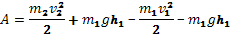
Где массы слоев раны 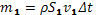и 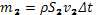, а h₁ и h₂ – высота сечений 1 и 2 относительно какого-либо нулевого уровня. Таким образом, получаем:

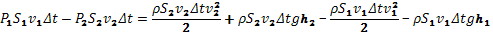
Сокращая на Δt и учитывая, что 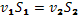, получаем:

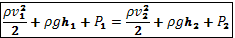
Это и есть уравнение Бернулли.

Величину можно назвать плотностью кинетической энергии, а величину 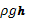- плотностью потенциальной энергии. Тогда можно написать: для стационарного течения идеальной жидкости сумма давления и плотностей кинетической и потенциальной энергий является постоянной для любого сечения потока жидкости.