Трубопроводы с насосной подачей жидкости

Схема к расчету трубопрово­да с путевым расходом

Трубопроводы с равномерно распределенным путевым расходом.

Это такие трубопроводы, в которых вдоль всего пути расход

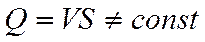
Расход в сечении А (рис.)

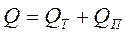
где Q_Т — транзитный расход; Qn — путевой расход.

Отношение путевого расхода Qn к длине трубопровода l назы­вают удельным расходом q.

С течением времени расход постепенно уменьшается и стано­вится равным Q_T в сечении В, а в произвольном сечении С расположенном на расстоянии х от начального сечения А расход жидкости

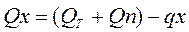
Потери напора по длине в трубопроводе для квадратичной области турбулентного режима

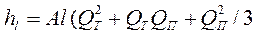
Если на участке АВ будет отобран весь расход, т. е. отсутству­ет транзитный расход (Q_T = 0), то потери напора по длине в данном частном случае примут вид формулы, которая носит название формулы Дюпуи:

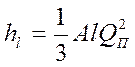
В случае расчета трубопроводов с путевым расходом с достаточной степенью точности Qп² /3 можно заменить членом Qп² /4. Тогда

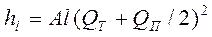
Расчетный расход на участке АВ

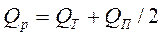
Анализ этой формулы показывает, что путевой расход Qп эквивалентен транзитному расходу и зависит от степени равно­мерности отбора жидкости по длине трубопровода.

Расчет кольцевой сети. Кольцевая сеть состоит из замкну­тых колец и магистралей, присоединенных к водонапорной баш­не или резервуару. Рассмотрим простейший случай расчета коль­цевой водопроводной сети, состоящей из магистрального трубо­провода А—В и одного кольца В—1—2—3—-4—В (рис.). Расход, забираемый в точках 1, 2, 3, 4, обозначим соответственно через Q₁, Q₂, Q₃, Q₄

На основании топографических данных, длины участков тру­бопровода, диаметра труб задаемся направлением движения во­ды по кольцу и нулевой (раз

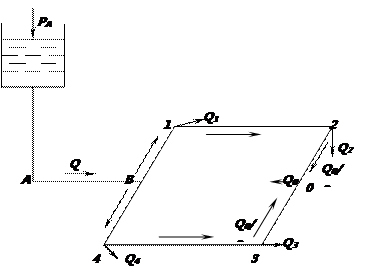
дельной) точкой сети. Нулевая точ­ка выбирается таким образом, чтобы потери напора в ветвях слева и справа от этой точки были одинаковыми. Далее, так же как и при расчете тупиковой сети, определяем диаметр труб и подсчитываем потери напора на каждом участке по левой и правой сторонам кольца.

Если нулевая точка О выб­рана правильно, то сумма по­терь напора по левой стороне кольца должна равняться сум­ме потерь напора по правой стороне кольца, т. е.

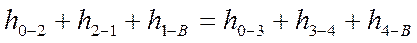
где h_0-2 и т.д. - потери на­пора по длине на соответствующем участке

Если это условие не выполняется, то расчет следует продол­жать до тех пор, пока не будет получено равенство потерь напора в двух рассматриваемых разомкнутых сетях.

В большинстве гидравлических систем технологического оборудования в качестве источника энергии используются насосы различного принципа действия. Важнейшей задачей, которая возникает при проектировании каждой гидросистемы, является согласование работы насосной станции и системы трубопроводов, гидроаппаратов и гидромашин, входящих в её состав. Это многообразные и сложные задачи, которые подробно рассматриваются в курсах, связанных с изучением гидропривода. Здесь мы познакомимся лишь с общим принципом таких расчётов.

Для этого рассмотрим наиболее простой случай трубопровода, по которому насос перекачивает жидкость из гидробака в ёмкость или полость с заданными величинами давления и расхода. К таким ёмкостям можно отнести, например, гидроцилиндр. Нивелирными высотами, как и в предыдущих случаях, пренебрежём из-за их малости.

Запишем сначала уравнение Бернулли для сечений 2 и 3

,

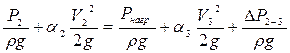где 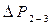- суммарные потери давления в напорном трубопроводе (характеристика напорного трубопровода).

Теперь запишем уравнение Бернулли для сечений 0 и 1

,

где 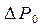- атмосферное давление,

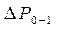- суммарные потери давления во всасывающем трубопроводе (характеристика всасывающего трубопровода).

Из второго уравнения определим общий напор (энергию), которым обладает жидкость при входе в насос. Тогда второе уравнение примет вид

.

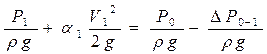В процессе своей работы насос передаёт жидкости дополнительную энергию H_насоса, в результате чего общий напор жидкости в сечении 2 становится равным:

,

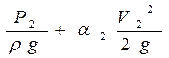т.е. можно записать:

.

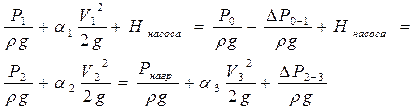Выделим из полученного равенства величину H_насоса:

.

Перегруппируем члены в этом выражении:

.

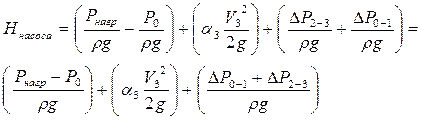Если принять, что:

§ в первом слагаемом атмосферное давление P₀ равно 0,

§ второе слагаемое (скоростной напор на выходе из напорного трубопровода) можно переписать через расход и представить в виде , где 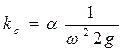можно считать коэффициентом скоростного напора (в этом выражении ω – площадь сечения трубопровода),

§ третье слагаемое можно представить в виде суммарной характеристики всасывающего и напорного трубопровода, то последнее выражение примет вид:

.

Последнее выражение представляет собой рабочуюхарактеристику насоса.

Построив характеристику трубопровода 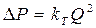и характеристику насоса можно найти так называемую рабочую точку, как точку пересечения характеристик насоса и трубопровода. Это означает, что при соответствующих этой точке давлении и расходе, будет обеспечиваться работа насоса с требуемыми характеристиками. Чтобы получить другую рабочую точку нужно или изменить рабочую характеристику насоса или характеристику трубопровода. Это можно сделать различными способами, например, изменив сопротивление трубопровода или режим работы насоса.