Результаты регрессионного анализа

Рис.3.

Рис.2.

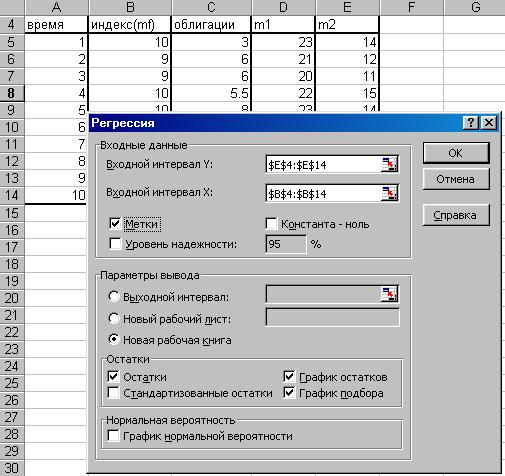
Рис.4. Заданы интервалы входных данных. ОК.

Результат регрессионного анализа содержится в таблицах 1-4. Рассмотрим содержание этих таблиц.

Во втором столбце таблицы 3 содержатся коэффициенты уравнения регрессии a₀, a_1. В третьем столбце содержатся стандартные ошибки коэффициентов уравнения регрессии, а в четвертом - t-статистика, используемая для проверки значимости коэффициентов уравнения регрессии.

	Коэффициенты	Стандартная ошибка	t-статистика
Y-пересечение	-1.633	2.412	-0.677
индекс(mf)	1.583	0.240	6.605

Уравнение регрессии зависимости доходности ценной бумаги TRUW (m₂) от индекса рынкаот индекса рынка m_r имеет вид

m₂ = - 1.63 + 1.58´m_r

Регрессионная статистика
Множественный R	0.919
R-квадрат	0.845
Нормированный R-квадрат	0.826
Стандартная ошибка	0.830
Наблюдения

Дисперсионный анализ
	df	SS	MS	F	Значимость F
Регрессия		30.083	30.083	43.625	0.000
Остаток		5.517	0.690
Итого		35.6

Собственный (или несистематический) риск ценной бумаги TRUWравен

s_e2² = Se²/N = 5.517/10 = 0.5517

Аналогично построим модель зависимости доходности ценной бумаги GLSYTR от индекса рынка.

m₁ = 4.667 + 1.833 ´m_r s_e1² = Se²/N = 7.667/10 = 0.767

Решение оптимизационной задачи. Необходимо найти вектор Х= (X₁, X₂), минимизирующий риск портфеля s_p. решение задачи можно получить в среде EXCEL с помощью надстройки Поиск решения.

Задача Марковица о формировании портфеля заданной эффективности с учетом ведущего фактора и минимального риска может быть сформулирована следующим образом:

Необходимо найти вектор Х= (X₁, X₂,… X_n), минимизирующий риск портфеля s_p.

s_p =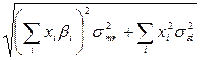

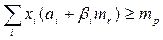
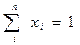
Экономико-математическая модель задачи.

X₁ - доля в портфеле ценных бумаг GLSYTr;

X₂ - доля в портфеле ценных бумаг Truw.

В нашей задаче задана эффективность портфеля не ниже, чем в среднем по облигациям, т.е. 6% (60/10=6%).

s_p =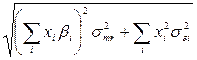= 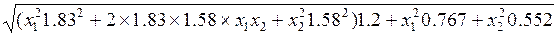Þmin

x₁ + x₂ = 1

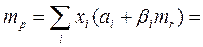
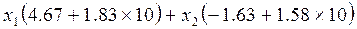³ 6

x_1, x₂³ 0

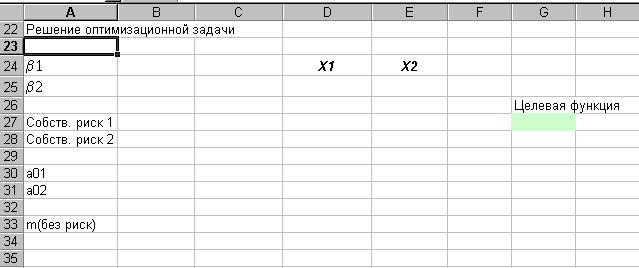
Рис.5. Подготовлена форма для ввода данных

Рис.6. Введены исходные данные. В ячейках D25 и E25 будут находиться значения неизвестных Х1 и Х2 (эти ячейки называются изменяемыми).

Целевая функция имеет вид:

s_p==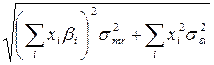

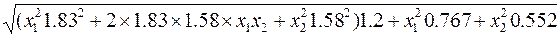
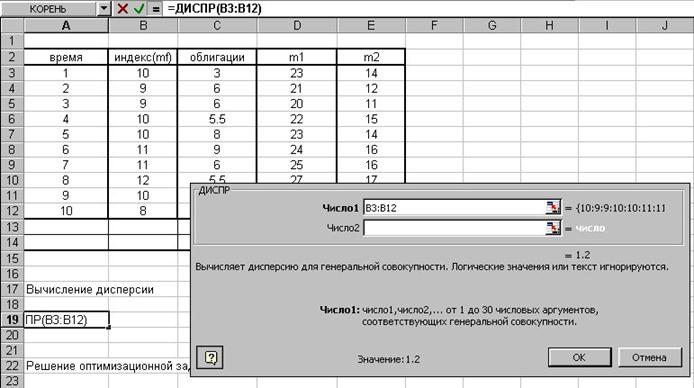
Рис.7. Для вычисления дисперсии воспользуемся функцией ДИСПР. Результат в ячейке А19.

Для ввода формулы воспользуемся функцией КОРЕНЬ.

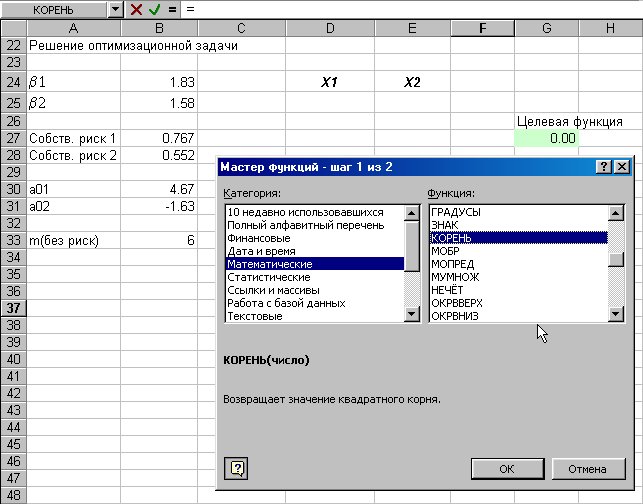
Рис.8. Ввод выражения для целевой функции (шаг1).

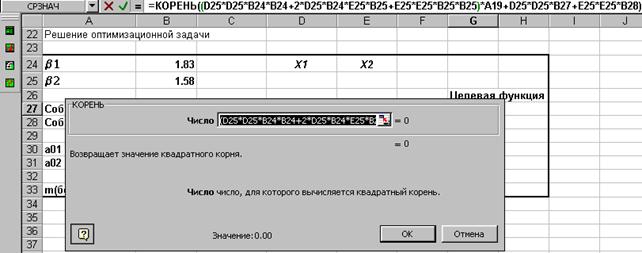
Рис.9. Далее вводим подкоренное выражение:

(D25*D25*B24*B24+2*B24*B25*E25*D25*+E25*E25*B25*B25)*A19+D25*D25*B27+E25*E25*B28) (шаг 2).

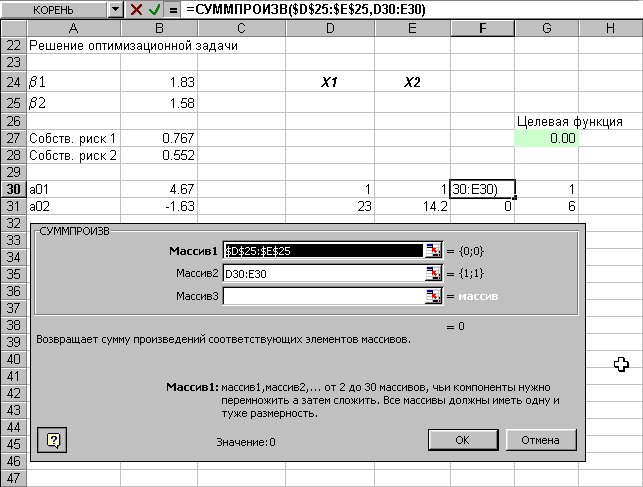
Рис.10. Введем зависимость для левых частей ограничений

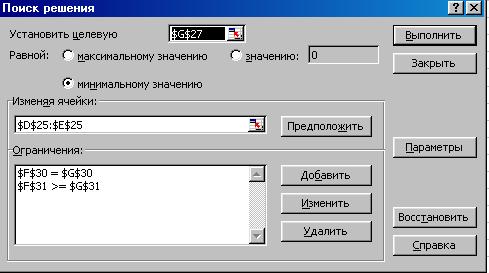
Рис.11. Указываем целевую ячейку (G27), изменяемые ячейки (D25:E25), и добавляем ограничения (рис.12)

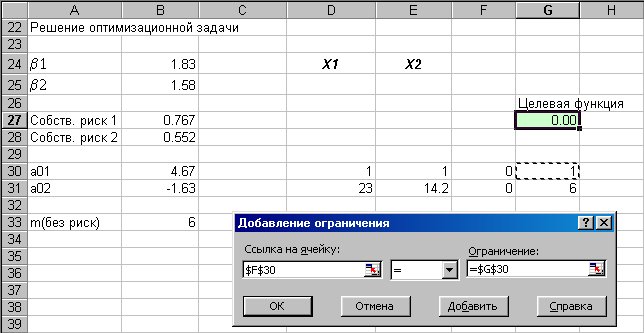
Рис.12. Добавляем ограничения

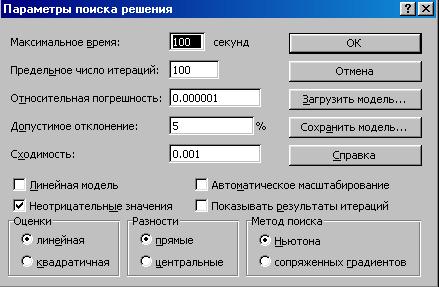
Рис.13. Указываем параметры.

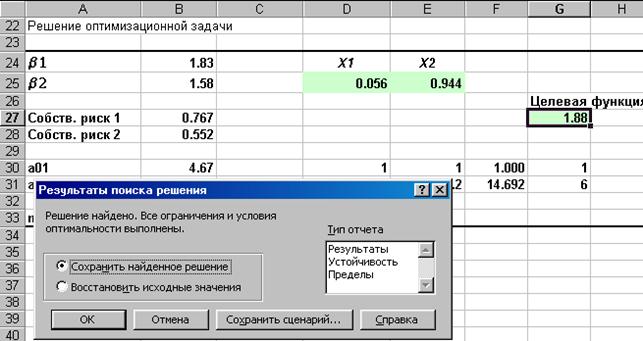
Рис.14. Решение найдено.

Решение оптимизационной задачи
b1	1.83		X1	X2
b2	1.58		0.056	0.944
						Целевая функция
Собств. риск 1	0.767					1.88
Собств. риск 2	0.552
a01	4.67				1.000
a02	-1.63			14.2	14.692
m(без риск)

Ответ: Минимальный риск портфеля равный 1.88 % будет достигнут, если доля акций GLSYTr составит 5.6%, а доля акций Truw – 94.4%.

Задания для аудиторной работы с применением ПЭВМ.

Номер вашего варианта соответствует последней цифре зачетной книжки.