Лекция 1
КОНСПЕКТЫ ЛЕКЦИЙ
МАТЕМАТИЧЕСКИЙ АНАЛИЗ
№ 1
| Содержание | ||
| 1. | Множество. Операции над множествами……………………………... | |
| 2. | Определение функции……………. | |
| 3. | Различные формы задания функции…………………………………. | |
| 4. | Четные, нечетные, периодические функции……………………………. | |
| 5. | График функции. Асимптоты……. |
Множество. Операции над множествами. Определение функции. Различные формы задания функции: явная, неявная, табличная, параметрическая. Четные, нечетные, периодические функции. График функции. Асимптоты.
Понятие множества в математике является первичным и, поэтому, не может быть определено через другие, более элементарные понятия. Множества в математике могут состоять из чисел, векторов, матриц, функций и других объектов.
Множества обозначаются прописными буквами 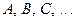 .
.
Объекты, из которых образовано множество, называются элементами множества или точками и обозначаются строчными буквами 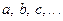 ;
; 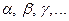 .
.
Если объект 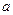 принадлежит множеству
принадлежит множеству 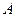 , это записывается таким образом:
, это записывается таким образом: 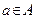 ; если объект
; если объект 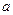 не принадлежит множеству
не принадлежит множеству 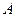 , это записывается таким образом:
, это записывается таким образом: 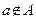 .
.
Множество, не содержащее ни одного элемента, называется пустым множеством и обозначается 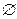 .
.
Множество 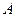 называется подмножеством множества
называется подмножеством множества 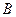 , если каждый элемент множества
, если каждый элемент множества 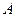 является одновременно элементом множества
является одновременно элементом множества 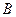 и обозначается
и обозначается 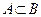 .
.
Множества 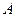 и
и 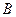 называются равными, если каждый из них является подмножеством другого и обозначается
называются равными, если каждый из них является подмножеством другого и обозначается 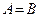 .
.
В математике удобно использовать теоретико-множественные и логические кванторы:
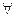 – квантор всеобщности, читается «для любого», «для всех», «для каждого»;
– квантор всеобщности, читается «для любого», «для всех», «для каждого»;
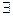 – квантор существования, читается «существует», «найдется», «имеется»;
– квантор существования, читается «существует», «найдется», «имеется»;
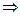 – квантор следствия, читается «следует», «вытекает», «если …, то …»;
– квантор следствия, читается «следует», «вытекает», «если …, то …»;
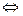 – квантор эквивалентности, читается «эквивалентно», «равносильно», «… тогда и только тогда, когда …».
– квантор эквивалентности, читается «эквивалентно», «равносильно», «… тогда и только тогда, когда …».
Определение подмножества можно записать следующим образом:
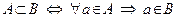 ,
,
а равенства множеств 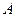 и
и  теперь можно записать так:
теперь можно записать так:
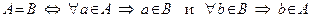 .
.
Множества можно задать различными способами:
если 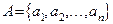 , то будем говорить, что множество задано перечислением элементов;
, то будем говорить, что множество задано перечислением элементов;
если 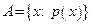 , то будем говорить, что множество задано характеристическим предикатом или множество задано с помощью некоторого свойства
, то будем говорить, что множество задано характеристическим предикатом или множество задано с помощью некоторого свойства 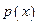 .
.
Примеры некоторых стандартных числовых множеств:
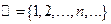 – множество натуральных чисел;
– множество натуральных чисел;
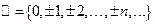 – множество целых чисел;
– множество целых чисел;
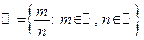 – множество рациональных чисел (множество десятичных бесконечных периодических дробей);
– множество рациональных чисел (множество десятичных бесконечных периодических дробей);
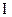 – множество иррациональных чисел (множество десятичных бесконечных непериодических дробей);
– множество иррациональных чисел (множество десятичных бесконечных непериодических дробей);
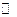 – множество вещественных чисел;
– множество вещественных чисел;
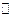 – множество комплексных чисел.
– множество комплексных чисел.
Стандартные числовые промежутки:
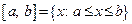 – отрезок;
– отрезок;
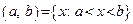 – интервал;
– интервал;
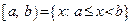 – полуинтервал;
– полуинтервал;
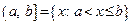 – полуинтервал;
– полуинтервал;
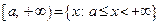 – замкнутая полуось;
– замкнутая полуось;
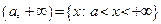 – открытая полуось;
– открытая полуось;
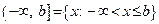 – замкнутая полуось;
– замкнутая полуось;
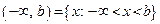 – открытая полуось;
– открытая полуось;
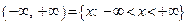 – числовая ось.
– числовая ось.
Пусть даны множество 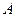 (Рис 1.) и множество
(Рис 1.) и множество 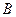 (Рис 2.).
(Рис 2.).
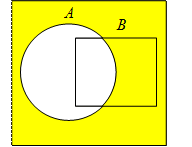
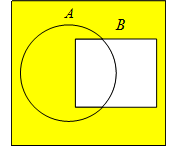
Рис. 1 Рис. 2
Объединением множеств 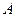 и
и 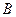 называется множество, если оно содержит только все элементы множества
называется множество, если оно содержит только все элементы множества 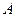 и все элементы множества
и все элементы множества 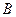 . Объединение множеств
. Объединение множеств 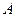 и
и 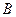 обозначается
обозначается 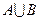 (Рис 3.).
(Рис 3.).
Пересечением множеств 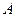 и
и 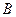 называется множество, если оно содержит только все элементы, принадлежащие множествам
называется множество, если оно содержит только все элементы, принадлежащие множествам 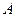 и
и 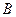 одновременно. Пересечение множеств
одновременно. Пересечение множеств 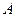 и
и 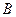 обозначается
обозначается 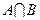 (Рис 4.).
(Рис 4.).
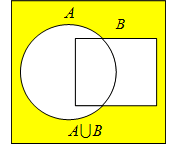
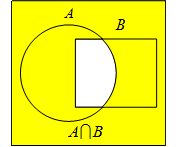
Рис. 3 Рис. 4
Разностью множеств 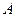 и
и 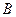 называется множество, если оно содержит только все элементы принадлежащие множеству
называется множество, если оно содержит только все элементы принадлежащие множеству 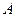 , не принадлежащие множеству
, не принадлежащие множеству 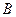 . Разность множеств
. Разность множеств 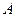 и
и 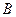 обозначается
обозначается 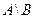 (рис. 5). На рис. 6 изображена разность
(рис. 5). На рис. 6 изображена разность 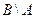 .
.

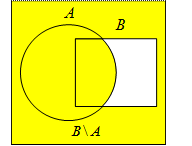
Рис. 5 Рис. 6
 2014-02-05
2014-02-05 327
327







