Контрольные вопросы к лекции 3
Рис.2.56. Пример диаграммы Боде
Рис.2.55.Иллюстрация запасов устойчивости на примере диаграммы Найквиста
Рис.2.53. Корневой годограф
Рис.2.52.Замкнутая система с цифровым регулятором
Рис.2.51.Примеры связи между расположение полюсов и временными характеристиками
Рис.2.50.Отображение линии постоянного коэффициента затухания на - плоскость
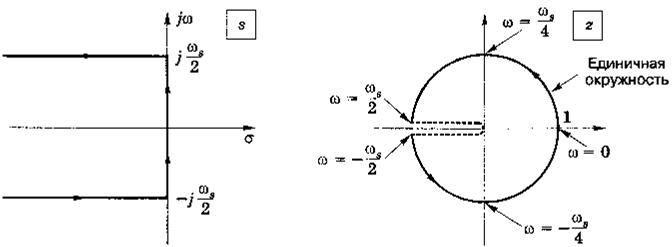
Рис.2.48.Отображение основной полосы с - плоскости на - плоскость
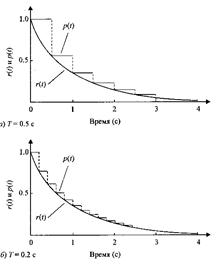
Рис.2.47. Реакция квантователя и экстраполятора нулевого порядка на сигналпри двух значениях периода квантования.
 Реакция экстраполятора нулевого порядка на единичный импульсный сигнал приведена на рис.2.45, а его передаточная функция имеет вид
Реакция экстраполятора нулевого порядка на единичный импульсный сигнал приведена на рис.2.45, а его передаточная функция имеет вид
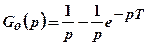 .
.
Цифровой компьютер и соответствующие преобразователи сигналов обладают ограниченной точностью. Под точностью в данном случае понимается разрешение, с которым определяются отдельные переменные, Так, точность компьютера ограничена конечной длиной машинного слова. Точность АЦП ограничена конечным числом двоичных разрядов его регистра. Поэтому говорят, что преобразованный сигнал 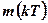 включает в себя ошибку квантования по амплитуде. Если эта ошибка, а также ошибка, обусловленная конечной длиной слова, малы в сравнении с амплитудой сигнала, то цифровая система является достаточно точной и эффектом квантования по амплитуде можно пренебречь.
включает в себя ошибку квантования по амплитуде. Если эта ошибка, а также ошибка, обусловленная конечной длиной слова, малы в сравнении с амплитудой сигнала, то цифровая система является достаточно точной и эффектом квантования по амплитуде можно пренебречь.
Замкнутая дискретная (цифровая) система устойчива, если все полюса её передаточной функции  расположены на
расположены на  - плоскости внутри единичной окружности (для
- плоскости внутри единичной окружности (для  - плоскости все полюса располагаются левее мнимой оси, которая и соответствует этой окружности) (рис.2.48).
- плоскости все полюса располагаются левее мнимой оси, которая и соответствует этой окружности) (рис.2.48).
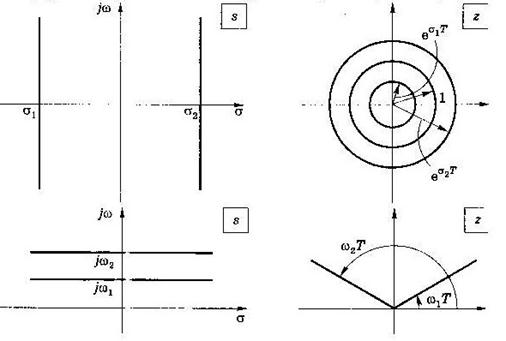
На рис.2.49, а и б отображены линии постоянного затухания и постоянной частоты на  - плоскость. На рис.2.50 – постоянного коэффициента затухания.
- плоскость. На рис.2.50 – постоянного коэффициента затухания.
 а
а
б
Рис.2.49.Отображение линий постоянного затухания (а) и постоянной частоты (б) на 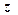 - плоскость
- плоскость
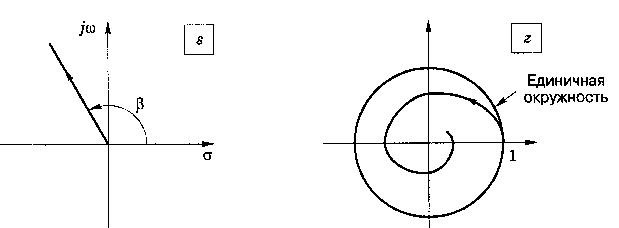
На рис.2.51 проиллюстрировано влияние расположение корней характеристического уравнения на переходные характеристики процессов.

Корневой годограф цифровой системы управления
Рассмотрим систему, изображённую на рис.2.52. В замкнутом состоянии система имеет передаточную функцию
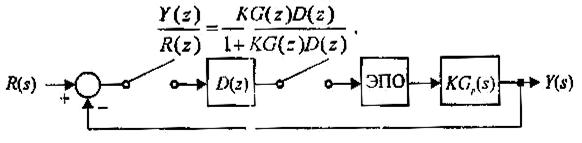
Характеристическое уравнение системы имеет вид 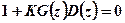 , что по форме аналогично характеристическому уравнению непрерывной системы, имеющей в разомкнутом состоянии передаточную функцию
, что по форме аналогично характеристическому уравнению непрерывной системы, имеющей в разомкнутом состоянии передаточную функцию 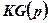 . Поэтому мы можем, варьируя коэффициентом усиления
. Поэтому мы можем, варьируя коэффициентом усиления  , построить корневой годограф дискретной системы, Правила построения корневого годографа приведены ниже.
, построить корневой годограф дискретной системы, Правила построения корневого годографа приведены ниже.
1. Корневой годограф начинается на полюсах и заканчивается в нулях передаточной функции 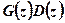 .
.
2. Корневой годограф включает в себя отрезки действительной оси, расположенные слева от нечёткого числа полюсов и нулей.
3. Корневой годограф симметричен относительно действительной оси.
4. Корневой годограф может отрываться от действительной оси и возвращаться на неё. Точки отрыва и точки входа определяются из уравнения 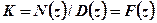 при
при 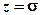 . Значения
. Значения 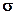 находятся путём решения
находятся путём решения 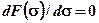 .
.
5. Точки принадлежащие корневому годографу, должны удовлетворять уравнению 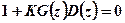 или
или 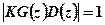 и
и 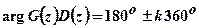 ,
, 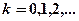
При 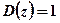 и
и 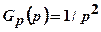 ,
, 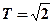 корневой годограф изображён на рис.2.53.
корневой годограф изображён на рис.2.53.
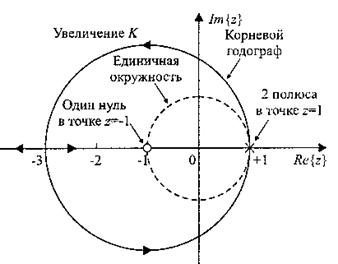 Положение на
Положение на  - плоскости полюсов и нуля этой функции показаны на рис.2.53. Характеристическое уравнение системы имеет вид
- плоскости полюсов и нуля этой функции показаны на рис.2.53. Характеристическое уравнение системы имеет вид 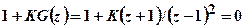 . Положим
. Положим 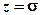 и выразим отсюда
и выразим отсюда  :
:
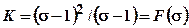 . Из условия
. Из условия 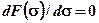 найдём корни
найдём корни 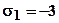 и
и 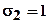 . Корни выходят из двух полюсов при
. Корни выходят из двух полюсов при 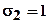 и возвращаются на действительную ось в точке
и возвращаются на действительную ось в точке 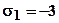 . Оба корня расположены вне единичной окружности, поэтому эта система неустойчива при любых значениях
. Оба корня расположены вне единичной окружности, поэтому эта система неустойчива при любых значениях 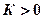 .
.
Синтез цифрового регулятора
Выберем регулятор с передаточной функцией 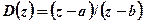 . Числитель выбирается так, чтобы сократить один из полюсов, лежащем на положительном направлении действительной оси; знаменатель выбираем так, чтобы обеспечить желаемое положение комплексных корней скорректированной системы внутри единичной окружности. Если
. Числитель выбирается так, чтобы сократить один из полюсов, лежащем на положительном направлении действительной оси; знаменатель выбираем так, чтобы обеспечить желаемое положение комплексных корней скорректированной системы внутри единичной окружности. Если 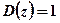 и
и 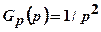 то система неустойчива. Если принять
то система неустойчива. Если принять 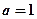 и
и 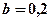 , то получим
, то получим 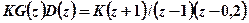 . Используя выражение для
. Используя выражение для 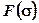 , найдём точку входа корневого годографа на действительную ось
, найдём точку входа корневого годографа на действительную ось 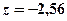 , как показано на рис.2.54. Единичную окружность годограф пересекает при
, как показано на рис.2.54. Единичную окружность годограф пересекает при 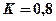 . Таким образом, система устойчива при
. Таким образом, система устойчива при 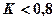 . Если принять
. Если принять 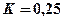 , то реакция системы на ступенчатый входной сигнал будет иметь перерегулирование 20% и время установления (по критерию 2%), равное 8,5 с.
, то реакция системы на ступенчатый входной сигнал будет иметь перерегулирование 20% и время установления (по критерию 2%), равное 8,5 с.
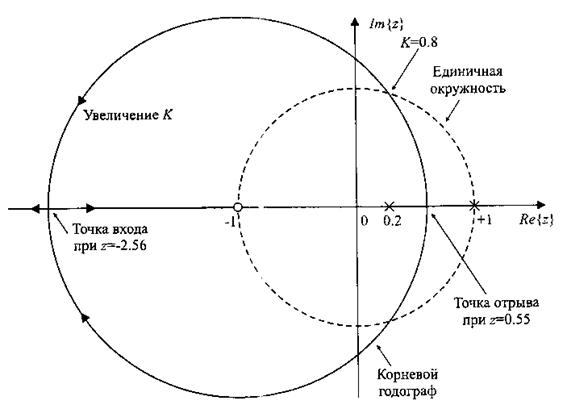
Рис.2.54.Корневой годограф (последний пример)
В непрерывных системах запас по модулю определяется как число, на которое надо умножить коэффициент усиления системы, чтобы достичь границы устойчивости. Запас по фазе определяется как угол, на который необходимо повернуть диаграмму Найквиста, чтобы она прошла через точку -1. Точно так же определяются запасы по модулю и по фазе для импульсных систем. Если посмотреть на диаграмму Найквиста на рис.2.55 то запас по модулю равен 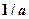 , а запас по фазе -
, а запас по фазе - 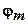 .
.
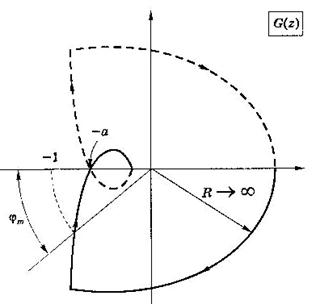 Информацию о частотных характеристиках замкнутой системы содержат как диаграмма Найквиста, так и диаграмма Боде. Эта информация одна и та же, только представлена в различных осях (рис.2.56).
Информацию о частотных характеристиках замкнутой системы содержат как диаграмма Найквиста, так и диаграмма Боде. Эта информация одна и та же, только представлена в различных осях (рис.2.56).
Цифровые регуляторы обладают большей гибкостью, поскольку для изменения какого-либо его параметры достаточно просто изменить число, записанное в ячейке памяти. Изменение параметра аналогового регулятора обычно требует замены по крайне мере одного элемента схемы.

Цифровые сигналы менее чувствительны к шумам и дрейфу параметров оборудования, т.к. данные представляются, генерируются, передаются и обрабатываются в виде двоичных слов.
Цифровая обработка сигналов производится с высокой скоростью и точностью. Повышение скорости цифровой обработки сигналов может быть достигнута за счёт аппаратных, а не программных средств.
Сложные алгоритмы обработки сигналов лучше реализовать с помощью цифровых устройств, т.к. при этом точность параметров ограничена лишь длиной слова цифрового процессора. Параметры же аналоговых процессоров в общем случае зависят от значений резисторов, конденсаторов и т.п.
Для синтеза цифрового ПИД - регулятора используются, в частности, передаточные функции операций численного интегрирования и дифференцирования: 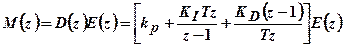 .
.
Структура такого регулятора показана на рис.2.57.
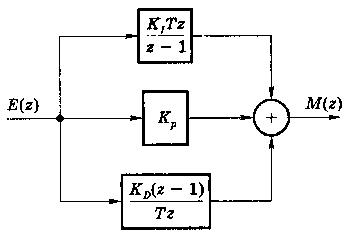 Рис.2.57.Цифровой ПИД - регулятор
Рис.2.57.Цифровой ПИД - регулятор
 2014-02-05
2014-02-05 908
908







