Природа ядерных сил

1. Квантовая модель электромагнитного (ЭМ) поля. Классическая электродинамика, в основе которой лежат уравнения Максвелла, учитывает только непрерывные свойства ЭМ-поля. В основе квантовой электродинамики лежит представление о том, что ЭМ-поле обладает также свойствами частиц. Носителями этих дискретных свойств являются кванты поля – фотоны, частицы с нулевой массой покоя и энергией E = hn. Спин фотонов равен 1.

Взаимодействие между электрически заряженными частицами квантовая электродинамика рассматривает как процесс обмена квантами поля – фотонами (обменное взаимодействие). Например покоящийся электрон с его электрическим полем может быть представлен уравнением: e^– e^– + hn (20.1)

Электрон последовательно испускает и поглощает квант поля с энергией hn. Хотя суммарная энергия фотона и электрона в правой части (20.1) больше, чем энергия покоящегося электрона, при осреднении во времени закон сохранения энергии не нарушается. Дело в том, что кванты ЭМ-поля, участвующие в обменном взаимодействии, считаются виртуальными (воображаемыми). Время их существования меньше времени Δ t, удовлетворяющего соотношению неопределённостей Гейзенберга (3.8), 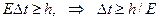. (20.2)

Поэтому виртуальный фотон не может быть обнаружен на опыте.

За определяемое условием (20.2) время Δ t виртуальный фотон может передать взаимодействие между точками на расстояние 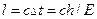. (20.3)

Энергия фотона E = hn может быть сколь угодно мала. Поэтому радиус действия ЭМ-сил является неограниченным. Если бы фотон имел массу покоя m ₀, то его энергия E = hn + m ₀ c ² не могла бы стать меньше величины m ₀ c ². Поэтому радиус действия обменных сил был бы ограничен величиной l_max = chçE_min = chçm ₀ c ² = L, (20.4)

где Λ = hçm ₀ c – комптоновская длина волны обменной частицы поля.

Ускоренно движущийся электрон (и любая другая электрически заряженная частица) наряду с виртуальными испускает и реальные фотоны, которые могут уходить на бесконечность, существовать сколь угодно долго и обнаруживаться в эксперименте.

2. Обменное взаимодействие между нуклонами в ядре. К началу 30-х годов XX в. квантовая электродинамика оказалась в состоянии правильно описать взаимодействие излучения с веществом (испускание, рассеяние и поглощение света). Она успешно решила проблему теплового излучения, комптоновского рассеяния ЭМ-излучения на свободных электрически заряженных частицах, проблему излучения и поглощения света атомами.

В 1934 г. Игорь Тамм высказал предположение, что взаимодействие между нуклонами в ядре также передаётся посредством каких-то виртуальных частиц. Из формулы (20.4) можно оценить их массу. Если допустить, что расстояние обменного взаимодействия составляет порядка размеров ядра, 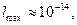то

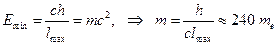
Кроме нуклонов в то время ещё были известны фотон, электрон, позитрон и нейтрино (последний ещё в стадии гипотезы). Ни одна из этих частиц не подходила.

В 1935 г. Хидеки Юкава обосновал гипотезу, что обменная частица с массой 200-300 электронных масс существует в природе, но пока не обнаружена. Эти предполагаемые частицы назвали мезонами (от греч. mesos – средний, то есть промежуточные по массе между нуклонами и электронами).

В 1936 г. Карл Андерсон совместно с С. Неддермайером открыли в космических лучах частицы с массой 207 m_e. Они назвали их m -мезонами. Оказалось, что m -мезоны (мюоны) существуют как положительно заряженные m ⁺, так и отрицательно заряженные m ^–. Их заряд по величине равен элементарному e, а массы одинаковы. Нейтрального мюона не существует. Период полураспада обоих мюонов одинаков и равен 2,2·10^–6 с. Спин мюонов ½. Теоретическая и экспериментальная проверка показала, что мюоны очень слабо взаимодействуют с нуклонами и не могут быть обменными частицами в ядре.

В 1947 г. Сесиль Пауэлл и Джузеппе Оккиалини открыли в космических лучах ещё один тип промежуточных частиц – p -мезоны (пионы). Именно эти частицы оказались носителями ядерных сил, предсказанными за 12 лет до того Юкавой.

Существуют положительные p ⁺, отрицательные p ^– и нейтральные p ⁰ мезоны. Заряд p ⁺ и p ^– мезонов равен элементарному заряду е. Масса заряженных пионов одинакова и равна 273 m_е. Масса нейтрального p ⁰ – пиона меньше и равна 264 m_е. Спин всех пионов равен 0. Все пионы нестабильны. Период полураспада заряженных пионов равен 2,60·10^–8с, нейтрального – 0,8·10^–16 с. Большинство заряженных пионов(99,9997 %) распадается по схемам:

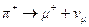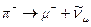, , где 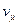- мюонное нейтрино, 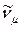- мюонное антинейтрино. (20.5)

Большинство нейтральных пионов (98,8%) распадаются на два γ-кванта. 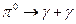(20.6)

Возможны 3 схемы обменного взаимодействия между нуклонами.

а. Взаимодействие посредством p ⁺ - мезона. p + n ↔ n + π⁺ + n ↔ n + p. (20.7)

Протон испускает виртуальный p ⁺ - мезон, превращаясь в нейтрон. Мезон поглощается нейтроном, который после этого превращается в протон. Затем такой же процесс идёт в обратном направлении. Каждый из взаимодействующих нуклонов часть времени проводит в заряженном состоянии, часть в нейтральном.

б. Взаимодействие посредством p ^– - мезона. n + p ↔ p + p ^– + p ↔ p + n (20.8)

Нейтрон испускает p ^– - мезон, превращаясь в протон. Протон поглощает p ^– - мезон, превращаясь в нейтрон.

в. Взаимодействие посредством p ⁰ – мезонов. p + n ↔ p + p ⁰ + n ↔ p + n, (20.9)

p + p ↔ p + p ⁰ + p ↔ p + p, n + n ↔ n + p ⁰ + n ↔ n + n. (20.10), (20.11)

Нуклоны обмениваются p ⁰ – мезонами в любом составе пары.

3. Доказательства в пользу обменного взаимодействия нуклонов. Взаимодействие посредством p ⁺ - мезона (случай а) подтверждается на опыте при рассеянии нейтронов на протонах. При прохождении пучка нейтронов через водород в этом пучке появляются протоны с той же энергией и направлением движения, что и у нейтронов в пучке. Расчет показывает, что число протонов больше, чем их может быть при лобовом выбивании нейтронами. Логично допустить, что нейтрон, пролетая вблизи протона, может захватывать его виртуальный p ⁺ - мезон, превращаясь в протон. Потерявший заряд протон превращается в нейтрон.

Идея обменного взаимодействия между нуклонами позволяет объяснить загадку магнитного момента у нейтрона (заряда нет, а магнитное поле есть) и аномально большую величину магнитного момента у протона. Допустим, что магнитный момент виртуального протона равен 1 М _я, магнитный момент виртуального нейтрона равен нулю, орбитальные магнитные моменты виртуальных p ⁺ и p ^– - пионов равны, соответственно, +3 М _я и –3 М _я. Тогда магнитный момент реального протона, согласно схеме p ↔ n + p ⁺, равен М _р = 0 + 3 М _я = 3 М _я (2,79 М _я на опыте). Магнитный момент реального нейтрона согласно схеме n ↔ p + p ^–, равен М_п = 1 М _я – 3 М _я = –2 М _я (–1,91 М _я на опыте).

(Следуя формальной логике, из опыта получается, что магнитный момент виртуального протона должен быть 0,88 М _я, а орбитальные моменты пионов ± 2,79 М _я).

4. Ядерные реакции – это процессы сильного взаимодействия атомного ядра с элементарной частицей или с другим ядром, приводящие к образованию новых ядер. Взаимодействие реагирующих частиц возникает при сближении их до расстояний порядка 10^–14 м благодаря действию ядерных сил. Характеризуются ядерные реакции эффективным сечением, энергией и временем (продолжительностью) реакции.

а. Эффективное сечение s. Пусть частица-снаряд, например нейтрон, падает нормально поверхности на мишень, имеющую форму плёнки площадью S и настолько малую толщину l, что ядра мишени не затеняют друг друга. Если полагать, что ядерная реакция происходит лишь тогда, когда частица-снаряд попадает внутрь некоторого объема ядра V = 4 p r ³ ç 3, то вероятность р того, что частица прореагирует с ядром, равна отношению суммы сечений этих объемов ядер к площади S мишени. 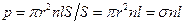. (20.12)

Здесь p r ² = s – эффективное сечение одного ядра, n – концентрация ядер (атомов) в мишени. В опыте эта вероятность равна отношению числа Δ N прореагировавших с ядрами частиц к числу N частиц, бомбардировавших мишень. 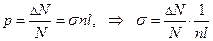. (20.13)

Величина s не имеет буквального смысла. Частица может пройти сквозь ядро по его центру и не прореагировать с ядром. В других случаях проходить за пределами s и прореагировать. Величина s имеет статистический смысл. С её помощью наглядно представляются и сравниваются вероятности протекания разных ядерных реакций.

Чтобы перейти к толстым мишеням, преобразуем выражение (20.13) к дифференциальному виду и проинтегрируем. Уменьшение – dN числа бомбардирующих частиц в бесконечно тонком слое мишени dl есть – dN = Nsndl. (20.14)

Это дифференциальная форма экспоненциального закона убывания потока N, известная в оптике как закон Бугера. После интегрирования при начальном условии N | _{t =0} = N ₀ получаем: 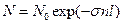. (20.15)

Формула (20.15) позволяет работать с толстыми мишенями и определять s по соотношению между падающим на мишень N ₀ и прошедшим мишень N потоками частиц.

В качестве единицы измерения эффективного сечения σ в ядерной физике исторически принят барн,1 барн = 10^—28 м².

б. Энергия в ядерных реакциях может выделяться (экзотермические реакции) и поглощаться (эндотермические реакции). Энергия реакции определяется разностью масс Δ m исходных и конечных частиц по формуле E = Δ mc ². Если сумма масс образующихся частиц меньше суммы масс исходных частиц, Δ m > 0, энергия выделяется. В противном случае энергия поглощается.

в. Время (продолжительность) ядерной реакции. В качестве единицы времени в ядерных реакциях используют ядерное время t. Это промежуток времени, который требуется нуклону с энергией 1 МэВ (скорость нуклона около 10⁷ м ç с), чтобы пройти расстояние, равное поперечнику ядра (10^–14 м). По порядку величины t» 10^–14 ç 10⁷ = 10^–21 с.

В зависимости от энергии бомбардирующих частиц ядерные реакции могут протекать по-разному. Различают 2 вида ядерных реакций: реакции через составное ядро и прямые ядерные реакции.

5. Реакции с образованием составного ядра. Первым ввёл представление о таком варианте протекания ядерной реакции Нильс Бор в 1936 г. Он предположил, что реакции, вызываемые не очень быстрыми частицами, протекают в 2 этапа. На первом этапе обстреливаемое ядро захватывает частицу-снаряд, которая, многократно сталкиваясь с нуклонами ядра, передаёт им свою энергию. В результате образуется возбуждённое составное ядро.

На втором этапе возбуждённое ядро переходит в основное состояние, испуская частицу. Это спонтанный переход статистического характера. Понятие составного ядра применяется лишь в тех случаях, когда период его полураспада Т» (10⁵ ¸ 10⁷)τ = 10^–16 ¸ 10^–14 с.

Если возбуждённое ядро испускает такую же частицу, какая была им захвачена, процесс называется рассеянием. В случае упругого рассеяния энергия частицы не меняется. Если энергия меняется, рассеяние называется неупругим. Собственно ядерной реакцией называется процесс, в котором поглощается одна частица, а испускается другая. Примером реакции через составное ядро является реакция открытия протона (Резерфорд, 1919 г.).

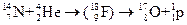. (20.16)

Вычислим дефект массы Δ m и энергию Е этой реакции.

Δ m = 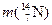+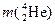––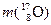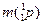= 14,0031 + 4,0026 – 16,9991 – 1,0078 = – 0,0012 а.е.м.

Масса образовавшихся продуктов реакции больше массы исходных компонентов. Следовательно, реакция эндотермическая, с поглощением энергии E = Δ mc ² = 1,2 МэВ. Если учесть, что энергия a -частиц составляла около 7,6 МэВ, а энергия образовавшихся протонов около 6 МэВ, то баланс энергии сходится, 7,6 МэВ = 6 МэВ + 1,2 МэВ +энергия отдачи ядра.

Реакции с образованием составного ядра обычно идут, когда кинетическая энергия частицы-снаряда не превышает 10 МэВ. С ростом энергии свыше 10 МэВ всё больший процент реакций приходится на прямые ядерные реакции.

6. Прямые ядерные реакции вызываются быстрыми частицами с энергией 10 МэВ и более. Эти реакции протекают в течение времени t порядка ядерного, t» t = 10^–21 c. В результате частица-снаряд успевает провзаимодействовать с одним - двумя периферийными нуклонами ядра. Например, в реакции подхвата налетевший на ядро протон откалывает от ядра нейтрон и захватывает его, образуя дейтрон. 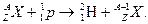(20.17)

Прямые ядерные реакции никогда не идут в чистом виде, они всегда конкурируют с реакциями через составное ядро. С изменением энергии частиц меняется соотношение между этими реакциями. Прямые процессы очень разнообразны. Они идут на всех ядрах при любых налетающих частицах. Вылетать из ядер могут одиночные нуклоны, дейтроны, тритоны, ядра 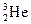, 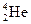и более сложные лития, бериллия и др. Крупные ядра–осколки называют фрагментами, а сам процесс – фрагментацией.

7. Примеры ядерных реакций. В зависимости от типа частицы-снаряда различают реакции под действием a -частиц, протонов, нейтронов, g -квантов и др.

а. Реакции под действием α-частиц исторически были первыми ядерными реакциями, открытыми в эксперименте. Альфа-частицы получали с помощью a - радиоактивных препаратов. Кроме реакции открытия протона

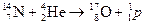(Э. Резерфорд, 1919) (20.18)

и нейтрона 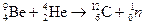(Дж. Чедвик, 1932) (20.19)

назовём ещё одну, в которой впервые был искусственно получен радиоактивный изотоп (Ирен и Фредерик Жолио-Кюри, 1934). 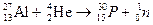. (20.20)

Изотоп фосфора 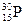распадается с периодом Т = 135,6 с, испуская позитроны. Это было первое наблюдение позитронов β ⁺ в ядерных реакциях после открытия их в космических лучах (К. Андерсон, 1932 г.).

б. Реакции под действием протонов. Протоны редко выбрасываются из ядер при их радиоактивных превращениях. Поэтому для получения пучка протонов их нужно ускорить электрическим полем. Первые ядерные реакции с искусственно ускоренными протонами осуществили в 1932 г. Джон Конкрофт и Эрнест Уолтон. 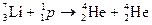. (20.21)

При обстреле протонами лития 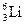был открыт изотоп гелия . .

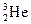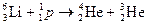в. Реакции под действием ускоренных дейтронов. В 1937 г. Эмилио Сегре с сотрудниками, обстреливая дейтронами изотоп молибдена 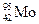, впервые получили химический элемент, которого нет в земной коре.

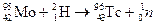. (20.22)

Это первый искусственно полученный элемент технеций. Он распадается с периодом Т = 4,3 дня.

г. Реакции под действием g -квантов называются фотоядерными. Они вызываются не ядерными, а электромагнитными взаимодействиями. Чтобы фотоядерная реакция могла идти, нужно, чтобы энергия g -кванта превосходила энергию освобождения какой-либо частицы. Энергия g -квантов, рождающихся в естественных ядерных превращениях, мала. Под действием естественных g -квантов идут только 2 реакции:

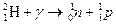, (20.23)

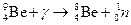. (20.24)

Более энергичные g -кванты получаются на ускорителях.

д. Реакции под действием нейтронов в виду их большого значения для ядерной энергетики будут рассмотрены в следующем параграфе.