Рис.131
Единица мощности экспозиционной дозы в СИ кулон на килограмм в секунду.
Внесистемная единица – рентген в час. 1 Р ç ч = 7,17 Кл ç кг·с. Мощность экспозиционной дозы 1 Р ç ч соответствует мощности поглощённой дозы 8,77·10–3 Гр ç 3600 с = 2,44 · 10–-6 Гр ç с.
9. Биологическое действие радиоактивного излучения было обнаружено и стало изучаться уже в первые годы после открытия радиоактивности. С началом применения атомного оружия в 1945 г., а затем и мирного использования атомной энергии эти исследования стали особенно интенсивными. Основные особенности биологического действия радиации сводятся к следующему:
а. Глубокие нарушения жизнедеятельности вызываются ничтожно малыми количествами энергии. Так, энергия, поглощённая телом млекопитающего или человека при облучении смертельной дозой, в случае превращения её в тепловую привела бы к нагреву тела всего на 0,001°С.
б. Радиация повреждает наследственный аппарат, её действие сказывается не только на облучённом индивиде, но и на его последующем потомстве.
в. Радиационное поражение носит латентный (скрытый) характер. Оно проявляется не сразу, а спустя какое-то время.
Взаимодействие радиации с биологическим объектом характеризуют эквивалентной дозой D э = kD, где D – поглощённая доза, k – так называемый коэффициент качества. Величина k тем больше, чем опаснее данный вид излучения для живого организма. Для β - и
g -лучей k = 1, для медленных нейтронов k = 3, для быстрых нейтронов и протонов k = 10, для осколков деления ядер k = 20.
Единица измерения эквивалентной дозы в СИ зиверт (Зв), 1 Зв = 1 Дж ç кг.
До последнего времени эквивалентная доза измерялась в бэрах. Бэр – аббривиатура фразы биологический эквивалент рада. 1 бэр = 0,01 Зв, 1 Зв = 100 бэр.
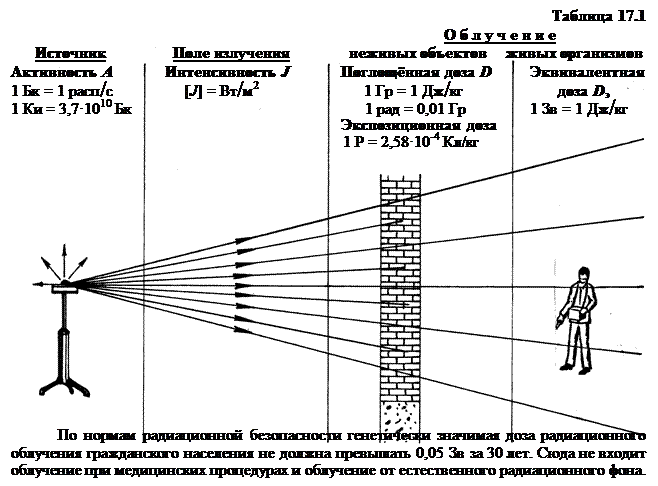
§18. Проблема строения атомного ядра
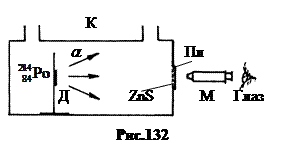 1. Открытие протона. В 1919 г. Эрнст Резерфорд впервые осуществил искусственное превращение ядер азота. Схема установки показана на рис.132. Альфа-активный препарат полоний
1. Открытие протона. В 1919 г. Эрнст Резерфорд впервые осуществил искусственное превращение ядер азота. Схема установки показана на рис.132. Альфа-активный препарат полоний 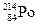 наносился на держатель Д внутри кюветы К. Сцинтилляции a -частиц могли наблюдаться на стеклянной пластинке Пл с порошком ZnS через микроскоп М. Альфа-частицы
наносился на держатель Д внутри кюветы К. Сцинтилляции a -частиц могли наблюдаться на стеклянной пластинке Пл с порошком ZnS через микроскоп М. Альфа-частицы 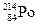 имеют энергию 7,58 МэВ и длину пробега в воздухе при нормальном давлении около 7 см. Держатель Д был установлен на таком расстоянии от пластинки Пл, что при пониженном давлении газа в кювете a -чаcтицы могли доходить до пластинки Пл и вызывать на ней сцинтилляции. При нормальном и повышенном давлении a -частицы до пластинки Пл не доходили.
имеют энергию 7,58 МэВ и длину пробега в воздухе при нормальном давлении около 7 см. Держатель Д был установлен на таком расстоянии от пластинки Пл, что при пониженном давлении газа в кювете a -чаcтицы могли доходить до пластинки Пл и вызывать на ней сцинтилляции. При нормальном и повышенном давлении a -частицы до пластинки Пл не доходили.
Кювета заполнялась разными газами, после чего наблюдались сцинтилляции a -частиц при малых давлениях и их исчезновение с ростом давления.
При заполнении кюветы азотом N2 на пластинке Пл наблюдались сцинтилляции и при давлениях, больших предельного. Поскольку a -частицы не могли дойти до люминофора, оставалось сделать предположение, что в процессе взаимодействия a -частиц с ядрами азота рождались какие-то другие ионизирующие частицы.
Наложение электрического и магнитного полей позволили установить, что рождающаяся новая частица имеет положительный заряд, равный по абсолютной величине заряду электрона, и массу, приблизительно равную массе водорода. Очевидно, это ядро атома водорода, как a -частица – ядро атома гелия.
Ещё в 1910-х годах была высказана идея, что ядра всех химических элементов состоят из ядер водорода – то есть ядер простейшего, первого в таблице элемента. Поэтому Резерфорд назвал новую частицу «протон», от греч. protos – первый. (Ещё раньше, в 1815 г., подобную идею в отношении состава химических элементов высказал химик Уильям Праут).
Патрик Блэкетт продолжил в 1925 г. опыты с азотом с помощью усовершенствованной им камеры Вильсона (см.с.132). Он автоматизировал съёмку туманных треков ионизирующих частиц двумя фотокамерами одновременно с разных направлений. Это позволило восстановить пространственную форму траекторий частиц. Просмотрев 23 000 снимков, он установил, что a -частица при столкновении поглощается ядром азота, после чего это новое ядро выбрасывает протон. С учётом сохранения заряда и массы ядерная реакция может быть записана так: 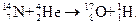 Резерфорд, 1919 г. Открытие протона (18.1)
Резерфорд, 1919 г. Открытие протона (18.1)
Энергия протонов в опытах Резерфорда составляла около 6 МэВ, а длина пробега 28 см.
2. Свойства протона. Протон в свободном состоянии – стабильная элементарная частица, ядро атома водорода. В ядерных реакциях обозначается часто символом 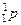 . Масса протона mp почти в 2000 раз превышает массу электрона me, mp = 1836 me = 1,67239 · 10–27 кг.
. Масса протона mp почти в 2000 раз превышает массу электрона me, mp = 1836 me = 1,67239 · 10–27 кг.
Спин, то есть собственный момент импульса протона такой же, как у электрона. Его проекция на физическую ось может принимать только два значения, Lsz =±ћ/ 2. Спиновое квантовое число s протона, как и у электрона, полуцелое, 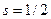 . Поэтому система протонов, как и система электронов, описывается статистикой Ферми-Дирака.
. Поэтому система протонов, как и система электронов, описывается статистикой Ферми-Дирака.
Магнитный спиновый момент протона. Как уже говорилось в §2, в теории атома водорода Бора орбитальный магнитный момент электрона в низшем энергетическом состоянии (n = 1) равен 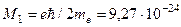 Дж ç Тл (см. ф. 2.18). На более высоком энергетическом уровне магнитный момент в n раз больше, где n – номер уровня, Mn = n·M 1. Минимальную величину магнитного момента
Дж ç Тл (см. ф. 2.18). На более высоком энергетическом уровне магнитный момент в n раз больше, где n – номер уровня, Mn = n·M 1. Минимальную величину магнитного момента 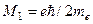 называют магнетоном Бора. Это минимальный магнитный момент в физике электронных оболочек атомов. Поэтому магнетон Бора используется в качестве единицы измерений магнитных моментов электронов.
называют магнетоном Бора. Это минимальный магнитный момент в физике электронных оболочек атомов. Поэтому магнетон Бора используется в качестве единицы измерений магнитных моментов электронов.
Из опытов Штерна и Герлаха по расщеплению атомных пучков в неоднородном магнитном поле следовало, что спиновый магнитный момент электрона равен магнетону Бора. Поэтому после открытия протона было естественным предположение, что спиновый магнитный момент протона определяется формулой магнетона Бора, в которой вместо массы электрона me должна стоять масса протона mp. 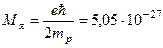 Дж ç Тл. (18.2)
Дж ç Тл. (18.2)
Величину М я называют ядерным магнетоном. Он в 1836 раз меньше магнетона Бора и используется в качестве единицы измерения магнитных моментов в ядерной физике.
Но измерения показали, что спиновый магнитный момент протона больше ядерного магнетона в 2,79 раз и составляет 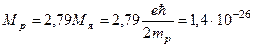 Дж ç Тл. (18.3)
Дж ç Тл. (18.3)
3. Ядерные реакции с испусканием протона наблюдались позднее при обстреле a -частицами бора 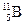 , фтора
, фтора 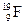 , натрия
, натрия 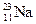 , алюминия
, алюминия 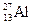 и фосфора
и фосфора 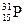 .
.
Заметим, что a -частицы могут результативно взаимодействовать лишь с лёгкими ядрами. Чтобы преодолеть электрическое отталкивание ядра, a -частица должна иметь кинетическую энергию Е, не меньшую потенциальной энергии необходимого для протекания реакции сближения с ядром. 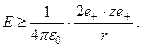 (18.4)
(18.4)
Отсюда можно найти максимальный номер Z элемента, ядро которого доступно для
a -частицы с энергией Е. 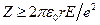 . (18.5)
. (18.5)
Радиус ядра 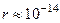 м. Для a -частиц с энергией Е ≈ 10 МэВ получаем
м. Для a -частиц с энергией Е ≈ 10 МэВ получаем
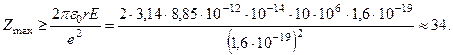
Это завышенное число. Как показывают опыты, эффективное взаимодействие
a -частиц с ядрами реально лишь для элементов с Z ≤ 20, то есть до кальция.
4. Открытие нейтрона. К 1930 г. выяснилось, что некоторые элементы, например, Be, Li, O2 при обстреле a -частицами протонов не испускают. Поэтому возник вопрос: что же происходит в тех случаях, когда обстреливаемое a -частицами ядро не выбрасывает протон?
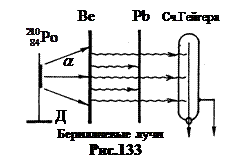
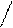
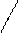 В 1930 г. Вальтер Боте и Ганс Бекер поставили опыт, схема которого показана на рис.133. На держателе Д помещался a -активный препарат
В 1930 г. Вальтер Боте и Ганс Бекер поставили опыт, схема которого показана на рис.133. На держателе Д помещался a -активный препарат  . Его особенность в том, что испытав a -распад ядро полония –210 превращается в ядро стабильного изотопа свинца
. Его особенность в том, что испытав a -распад ядро полония –210 превращается в ядро стабильного изотопа свинца 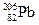 . Поэтому никаких других излучений препарат полония –210 не даёт. Энергия a -частиц у
. Поэтому никаких других излучений препарат полония –210 не даёт. Энергия a -частиц у  меньше, чем у
меньше, чем у 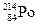 , она составляет 5,25 МэВ. Но для проникновения в ядра выбранного для опытов лёгкого бериллия, у которого Z = 4, этого было достаточно.
, она составляет 5,25 МэВ. Но для проникновения в ядра выбранного для опытов лёгкого бериллия, у которого Z = 4, этого было достаточно.
Было опасение, что ядра, не испускающие протоны, испускают другое излучение, не дающее вспышек в сернистом цинке ZnS. Поэтому экран из сернистого цинка был заменён счётчиком Гейгера. Его действие основано на том, что ядерная частица, влетающая внутрь счётчика, ионизирует находящийся в нём газ. В результате в цепи счётчика возникает импульс тока (подробнее о счётчике Гейгера см. с.130).
При облучении a -частицами пластинок из бериллия 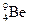 , бора
, бора 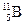 , лития
, лития 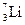 , как показал опыт, возникает какое-то излучение, вызывающее слабые разряды счётчика Гейгера. Особенно сильное излучение давал бериллий. Эти бериллиевые лучи обладали огромным проникающим действием: пластина свинца толщиной 2 см уменьшала их интенсивность всего на 14%.
, как показал опыт, возникает какое-то излучение, вызывающее слабые разряды счётчика Гейгера. Особенно сильное излучение давал бериллий. Эти бериллиевые лучи обладали огромным проникающим действием: пластина свинца толщиной 2 см уменьшала их интенсивность всего на 14%.
Боте и Бекер предположили, что бериллиевые лучи представляют собой очень жёсткие g -кванты. По поглощению в свинце было найдено, что их энергия составляет 7 МэВ. Но энергия  a -частиц составляла 5,25 МэВ. Откуда же взялся прирост энергии?
a -частиц составляла 5,25 МэВ. Откуда же взялся прирост энергии?
В 1931 г. к исследованиям бериллиевых лучей присоединились Ирен и Фредерик Жолио-Кюри. Помещая вместо свинцовых пластин листы парафина, они обнаружили, что из парафина под действием бериллиевых лучей исходили протоны, максимальный пробег в воздухе которых составлял 26 см. Такому пробегу соответствовала энергия протона 4,5 МэВ.
Парафины – это насыщенные углеводороды с общей формулой СnH2n+2. В них большое число атомов водорода. Появление протонов при облучении парафина бериллиевыми лучами супруги Кюри истолковали как результат комптоновского рассеяния g -квантов на протонах – ядрах атомов водорода. Протон отдачи уходит вперёд, когда рассеянный g -квант отражается назад, θ = π. Отсюда 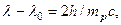 где mp – масса протона, λ 0 – длина волны бериллиевых g -квантов. Энергия Е выбитого протона должна быть равной убыли энергии g -кванта,
где mp – масса протона, λ 0 – длина волны бериллиевых g -квантов. Энергия Е выбитого протона должна быть равной убыли энергии g -кванта, 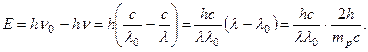 (18.6)
(18.6)
Допустим, что 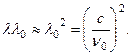 Тогда
Тогда 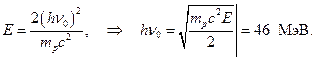
Итак, энергия бериллиевых g -квантов, вычисленная по поглощению в свинце, 7 МэВ, по энергии выбитых из парафина протонов – 46-48 МэВ. Кроме того получается, что α -частицы с энергией 5,25 МэВ выбивает g -квант с энергией 46-48 МэВ!
В 1932 г. в исследования природы бериллиевых лучей включается Джеймс Чедвик. Схема его установки практически ничем не отличалась от схемы Боте и Бекера, только вместо счётчика Гейгера он, как и Кюри, использовал ионизационную камеру. Чедвик исследовал рассеяние бериллиевых лучей не только парафином, но и другими веществами. Энергия g -квантов, измеренная по энергии ядер отдачи азота оказалась равной hν = 150 МэВ.
Итак, гипотеза, согласно которой бериллиевые лучи есть g -кванты, приводила к противоречивым результатам. В зависимости от метода измерения энергия g -квантов получалась разной и составляла 7, 48, 150 МэВ. Это доказывало неправильность данной гипотезы.
В том же 1932 г. Чедвик пришёл к выводу, что бериллиевое излучение есть поток нейтральных частиц, которые он назвал нейтронами. Обозначают нейтроны символом 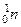 . Ядерную реакцию рождения нейтронов можно записать так:
. Ядерную реакцию рождения нейтронов можно записать так:
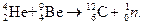 Реакция открытия нейтронов, 1930-32 г. (18.7)
Реакция открытия нейтронов, 1930-32 г. (18.7)
Чедвик выполнил и первые измерения массы нейтрона. Оказалось, что масса нейтрона близка к массе протона. Точное значение массы нейтрона было получено из баланса масс различных ядерных реакций с участием нейтронов.
5. Свойства нейтрона. Свободный нейтрон– нестабильная элементарная частица, распадающаяся на протон, электрон и электронное антинейтрино. 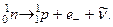 (18.8)
(18.8)
Среднее время жизни нейтрона τ ≈ 16 минут. Масса нейтрона несколько больше массы протона и составляет mn = 1838 me = 1,6760 · 10–27 кг. Спин нейтрона составляет ħç 2. Поэтому нейтроны, как электроны и протоны, описываются статистикой Ферми-Дирака.
Отношение спиновых магнитных моментов протона и нейтрона составляет
MpçMn = - 3 ç 2. «Минус» означает, что направления собственных механического и магнитного моментов нейтрона противоположны.
Высокая проникающая способность нейтронов объясняется отсутствием у них электрического заряда. Нейтроны практически не взаимодействуют с электронными оболочками атомов и в отличие от a -частиц и протонов не отталкиваются от ядер. Поэтому даже при малых энергиях нейтроны могут вплотную подходить к атомным ядрам и захватываться ими.
Для регистрации быстрых нейтронов используют их упругие столкновения с ядрами водорода. Благодаря практическому равенству масс протона и нейтрона при упругом ударе нейтрона с неподвижным протоном последнему передаётся большая часть кинетической энергии нейтрона. В результате нейтрон практически останавливается, а протон движется в том же направлении с энергией, близкой к первоначальной энергии нейтрона. По пути протон производит интенсивную ионизацию и потому может регистрироваться ионизационной камерой, счётчиком Гейгера или камерой Вильсона.
После нескольких последовательных столкновений с атомными ядрами быстрые нейтроны отдают свою избыточную энергию и в дальнейшем совершают хаотическое движение с тепловыми скоростями. Для таких тепловых нейтронов описанный выше метод регистрации путём рассеяния на ядрах атомов водорода непригоден. В этом случае используют ядерные реакции, при которых нейтрон, проникая в ядро, приводит к вылету из последнего a -частицы большой энергии. Например, 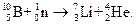 (18.10)
(18.10)
6. Проблема строения ядра. К началу 30-х годов XX в. были открыты следующие структурные элементы атома: электрон, 1897 г., Томсон; протон, 1919 г., Резерфорд;
нейтрон, 1932 г., Чедвик. Открытие радиоактивности и наблюдение первых ядерных реакций сделали актуальным вопрос: как устроено атомное ядро?
Прежде всего стало очевидно, что ядро атома нельзя представлять в виде шара, сложенного из неких неподвижных ядерных кирпичей. Ядро атома – это очень малый объём пространства, в котором движутся ядерные элементы. То есть это система ядерных объектов, движущихся и взаимодействующих по каким-то, пока ещё неизвестным законам.
В первую очередь надо было ответить на вопрос: из каких частиц состоит ядро. Исторически были рассмотрены два варианта: протон-электронное и протон-нейтронное ядро.
а. Протон-электронное ядро. Ещё до открытия нейтрона в 1930 г. Поль Дирак проанализировал идею Праута о том, что все химические элементы состоят из водорода. Применительно к проблеме строения ядра эта идея сводилась к тому, что все ядра элементов состоят из ядер атома водорода, то есть из протонов. (Изотоп водорода дейтерий 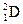 был открыт только через 2 года). Но это значит, что порядковый номер элемента в таблице Менделеева должен быть равен его массовому числу. Но таких элементов в таблице нет. Уже у гелия порядковый номер Z = 2, а массовое число А = 4. Как будто из 4-х протонов в ядре 2 нейтрализованы. Можно предположить, что ядро гелия содержит 4 протона и 2 электрона. Но в этом случае появляются противоречия с принципом неопределённости Гейзенберга. Действительно, неопределённость импульса в ядре, выраженная из соотношения неопределённостей для координаты-импульса
был открыт только через 2 года). Но это значит, что порядковый номер элемента в таблице Менделеева должен быть равен его массовому числу. Но таких элементов в таблице нет. Уже у гелия порядковый номер Z = 2, а массовое число А = 4. Как будто из 4-х протонов в ядре 2 нейтрализованы. Можно предположить, что ядро гелия содержит 4 протона и 2 электрона. Но в этом случае появляются противоречия с принципом неопределённости Гейзенберга. Действительно, неопределённость импульса в ядре, выраженная из соотношения неопределённостей для координаты-импульса 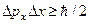 есть:
есть: 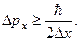 (18.11)
(18.11)
Но неопределённость координаты Δ х не может быть больше радиуса ядра, по крайней мере Δ х ≈ r 0. Из опытов Резерфорда 1909 г. r 0 ≈ 10–15 м. Импульс электрона в ядре не может быть меньше неопределённости импульса, 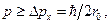 а его минимальная скорость движения из релятивистской формулы
а его минимальная скорость движения из релятивистской формулы 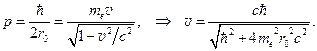 (18.12)
(18.12)
Здесь me – масса покоя электрона. После вычислений получаем v = 0,99998 c, где с – скорость света. Вычисленная по релятивистской формуле кинетическая энергия электрона в ядре составляет 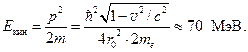
Но электроны, вылетающие из ядра при β -распаде, имеют энергию в пределах 10 МэВ. Столь разительному несоответствию очень трудно найти убедительное объяснение.
Вторая трудность протон-электронной модели ядра носит название азотной катастрофы. Суть её в следующем.
По величине сверхтонкого расщепления атомных спектров удалось вычислить магнитный момент атомных ядер. Он оказался примерно в 1000 раз меньше спинового магнитного момента электрона. Если в ядре чётное число электронов, то столь малый, магнитный момент ядра можно объяснить тем, что электроны в ядре образуют пары с противоположными спинами, поэтому магнитный момент ядра складывается из моментов протонов. А магнитный момент протона в 658 раз меньше момента электрона.
Но в ядре атома азота 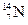 должно быть 14 протонов и 7 электронов. Если 6 электронов образуют пары с противоположными спинами, то один электрон остаётся неспаренным. Этот неспаренный электрон должен обеспечить ядру азота такой же магнитный момент, какой он имеет, то есть в 1000 раз больше, чем у ядер с чётным числом электронов. Но этого нет. Магнитный момент ядра азота того же порядка, что и у других ядер.
должно быть 14 протонов и 7 электронов. Если 6 электронов образуют пары с противоположными спинами, то один электрон остаётся неспаренным. Этот неспаренный электрон должен обеспечить ядру азота такой же магнитный момент, какой он имеет, то есть в 1000 раз больше, чем у ядер с чётным числом электронов. Но этого нет. Магнитный момент ядра азота того же порядка, что и у других ядер.
б. Протон-нейтронное ядро. Менее чем через полгода после открытия нейтрона практически одновременно и независимо друг от друга Дмитрий Иваненко и Вернер Гейзенберг предложили протон-нейтронный состав ядра. Разработанная позднее протон-нейтронная модель ядра прекрасно соответствует эксперименту и является сейчас общепринятой. Согласно этой модели ядро атома содержит Z протонов и A – Z нейтронов. Здесь Z – порядковый номер элемента в таблице Менделеева. Заряд ядра q = Ze+, поэтому номер Z называют часто зарядовым числом. Величину А называют массовым числом. Это целое число, равное атомной массе элемента, выраженной в углеродных единицах и округлённой до целого числа. Протоны и нейтроны, находящиеся в составе ядра, называют нуклонами (от лат. nucleus – ядро). Тем самым подчёркивается, что протон и нейтрон в составе ядра – это одна и та же частица в разных состояниях. Массовое число А есть число нуклонов в ядре. В зависимости от соотношения между количествами протонов и нейтронов в ядрах различают изотопы, изобары и изотоны.
Изотопы (от греч. isos – равный, topos –место) – ядра, содержащие одинаковое количество протонов, то есть имеющие одинаковый номер Z, и разное число нейтронов. Все изотопы помещаются в одной клетке таблицы Менделеева и являются разновидностями одного химического элемента. Различаются изотопы числом N нейтронов в ядре. Например, изотопы водорода:
Протий, 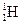 , ядро-протон, Z = 1, A = 1, N = A–Z = 0, нейтронов нет.
, ядро-протон, Z = 1, A = 1, N = A–Z = 0, нейтронов нет.
Дейтерий, 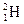 , ядро-дейтрон, Z = 1, A = 2, N = 1, один нейтрон.
, ядро-дейтрон, Z = 1, A = 2, N = 1, один нейтрон.
Тритий, 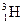 , ядро-тритон, Z = 1, A = 3, N = 2, два нейтрона.
, ядро-тритон, Z = 1, A = 3, N = 2, два нейтрона.
Изотопы гелия:
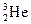 , Z = 2 (два протона), A = 3, N = 1 (один нейтрон), стабилен.
, Z = 2 (два протона), A = 3, N = 1 (один нейтрон), стабилен.
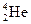 , Z = 2, A = 4, N = 2 (два нейтрона), стабилен.
, Z = 2, A = 4, N = 2 (два нейтрона), стабилен.
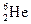 , Z = 2, A = 6, N = 4 (четыре нейтрона), нестабилен.
, Z = 2, A = 6, N = 4 (четыре нейтрона), нестабилен.
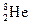 , Z = 2, A = 8, N = 6 (шесть нейтронов), нестабилен.
, Z = 2, A = 8, N = 6 (шесть нейтронов), нестабилен.
У известных ныне элементов число Z достигает примерно значения 105. На это число элементов приходится примерно 1500 известных изотопов. В среднем на один элемент –
14 изотопов. Из них 1 ç 5 – стабильных и 4 ç 5 – нестабильных.
Изотопы одного химического элемента имеют одинаковые химические и почти одинаковые физические свойства. Поэтому разделение изотопов – сложная физико-химическая задача. Наиболее заметно различаются изотопы водорода.
Изобары (от изос- и греч. baros – тяжесть) – ядра с одинаковым массовым числом А. Например, тритий 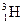 и гелий
и гелий 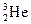 . У них по 3 нуклона, но соотношение между протонами и нейтронами разное. У трития Z = 1, N = 2, у гелия
. У них по 3 нуклона, но соотношение между протонами и нейтронами разное. У трития Z = 1, N = 2, у гелия 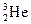 Z = 2, N = 1.
Z = 2, N = 1.
Изотоны – ядра с одинаковым числом нейтронов. Как и изобары, изотоны – это ядра разных химических элементов. Например, ядра 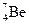 и
и 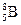 содержат по 3 нейтрона.
содержат по 3 нейтрона.
Слова изобары и изотоны используются много реже, чем слово изотопы.
1. Размеры ядер определяют тремя способами: рассеянием на ядрах быстрых электронов, исследованием спектров мезоатомов и дифракцией на ядрах нейтронов.
а. Рассеивание на ядрах быстрых электронов позволяет определить электрический радиус ядра R эл. Электроны, энергия которых должна быть не менее 100 МэВ, испытывают с ядром электромагнитное, но не ядерное взаимодействие. Поэтому по их рассеиванию можно судить фактически лишь о распределении протонов в ядре.
б. Спектры мезоатомов, то есть атомов, один из электронов в которых заменён мюоном. Мюон µ - элементарная частица, её заряд равен заряду электрона, а масса в 207 раз больше, mμ = 207 me. Как и электрон, мюон не участвует в ядерных взаимодействиях. Спектры мезоатомов дают больше информации о структуре ядра, чем спектры обычных атомов, поскольку мюон из-за своей большей массы движется в 207 раз ближе к ядру, чем электрон. Относительно заметное время мюон проводит даже внутри ядра.
в. Дифракция на ядрах нейтронов с энергией порядка 20 МэВ имеет то достоинство, что нейтроны испытывают ядерное взаимодействие с ядром. Радиус этого взаимодействия очень мал. Поэтому нейтроны заметно дифрагируют на ядре, то есть отклоняются от прямолинейного движения, лишь пролетая очень близко к ядру и внутри самого ядра. По ширине дифракционного максимума, который формируют нейтроны, прошедшие как вне, так и внутри ядра, можно оценить и размеры, и степень прозрачности ядра для нейтронов.
Дифракция нейтронов на ядрах позволяет определить радиус области, в которой действуют ядерные силы притяжения. Фактически это область, в которой сосредоточены нуклоны ядра. Из опытов следует, что радиус ядра пропорционален кубическому корню из числа A содержащихся в нём нуклонов, 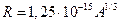 м. (19.1)
м. (19.1)
Вычислим концентрацию нуклонов в ядре. Для этого массовое число A надо разделить на объём ядра. 
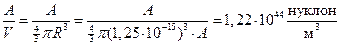 .
.
Умножив на массу одного нуклона mp = 1,67·10-27 кг, получаем среднюю плотность ρ ядерного вещества. 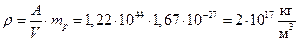 .
.
Плотность ядерного вещества не зависит от числа нуклонов в ядре. Она одинакова во всех ядрах и представляет собой гигантскую величину. Один кубический миллиметр такого вещества имел бы массу 200000 тонн. То, что плотность ρ ядерного вещества постоянна, свидетельствует о том, что нуклоны в ядре в смысле упаковки похожи на молекулы жидкости. Средний объём, приходящийся на один нуклон в ядре, не зависит от размера ядра, как средний объём, приходящийся на молекулу в жидкости, не зависит от размера капли.
2. Ядерные силы. Опыты Резерфорда 1909г. по рассеиванию a -частиц показали, что закон Кулона выполняется в микромире вплоть до размеров ядер. Но это значит, что между протонами в ядре должны действовать огромные силы отталкивания. Найдём величину этих сил для двух протонов в ядре гелия. Число нуклонов в ядре гелия 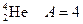 . Из формулы (19.1) радиус ядра гелия R = 1,25·10-15·41/3 = 2·10-15 м. Примем, что протоны находятся на концах диаметра ядра 2 R = 4·10-15 м. Тогда сила отталкивания между ними составляет:
. Из формулы (19.1) радиус ядра гелия R = 1,25·10-15·41/3 = 2·10-15 м. Примем, что протоны находятся на концах диаметра ядра 2 R = 4·10-15 м. Тогда сила отталкивания между ними составляет:
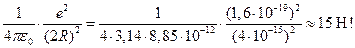 Почему же ядро, несмотря на столь большое взаимное отталкивание протонов, не разлетается на составлные части?
Почему же ядро, несмотря на столь большое взаимное отталкивание протонов, не разлетается на составлные части?
Наблюдаемая на опыте устойчивость ядер означает, что кроме электрических сил отталкивания между ядерными частицами действуют ещё силы притяжения. Это не могут быть силы гравитационного притяжения. Их потенциальная энергия
– Gmp /2 R = – 6,7·10-11·(1.7·10-27)2/4·10-15 = – 5·10-50 Дж, тогда как потенциальная энергия отталкивания протонов составляет (1/4 πε 0)/(e 2/2 R) ≈ 6·10-14 Дж! Это на 36 порядков больше.
Следовательно, в случае атомных ядер мы сталкиваемся с новым, особым видом взаимодействия. Это взаимодействие называется сильным, а отвечающие ему силы – ядерными. Полная теория ядерных сил не построена до сих пор, хотя достигла больших успехов в объяснении и прогнозировании многих опытных фактов. Основные современные представления о ядерных силах сводятся к следующему:
а. Существование ядерного поля. Подобно тому, как электрические силы обусловлены существованием материального электромагнитного поля, ядерные силы обусловленны существованием материального ядерного поля. Источниками ЭМ-поля являются любые электрически заряженные частицы вещества – электроны, протоны и др. Источниками ядерного поля являются нуклоны – протоны и нейтроны. Нуклоны обладают специфическим ядерным зарядом.
б. Зарядовая независимость ядерных сил. Ядерный заряд нуклонов одинаков по величине и знаку. Он не зависит от того, обладает нуклон электрическим зарядом (протон) или нет (нейтрон). С помощью ядерных сил нейтрон с нейтроном, нейтрон с протоном и два протона взаимодействуют одинаково.
в. Короткодействие ядерных сил. По сравнению с кулоновскими и гравитационными силами, которые убывают пропорционально квадрату расстояния между точечными источниками (зарядами, массами), ядерные силы убывают много быстрее. Они очень велики на расстояниях порядка поперечника ядра, но уже на расстоянии трёх поперечников практически незаметны. При сближении нуклонов притяжение сменяеться отталкиванием.
г. Ядерные силы не являются центральными. Электрическое поле вокруг точечного заряда и гравитационное поле вокруг точечных масс центрально симметричны. Ядерное поле отдельного нуклона не обладает центральной симметрией. Это связано с наличием у нуклонов спинового механического и магнитного моментов. Взаимодействие между нуклонами зависит от ориентации их спинов. Например, нейтрон и протон удерживаются вместе в ядре тяжёлого водорода – дейтрона только в случае, когда их мех.спины параллельны друг другу.
д. Свойство насыщения ядерных сил. Как известно, энергия взаимодействия двух электрических зарядов не зависит от наличия третьего (принцип суперпозиции). При внесении каждого последующего заряда энергия системы увеличивается пропорционально величине вносимого заряда. Каждый электрический заряд может взаимодействовать с неограниченным числом других зарядов. Насыщения электрических сил нет.
Насыщение ядерных сил состоит в том, что каждый нуклон в ядре может взаимодействовать с ограниченным числом нуклонов. Это чем-то похоже на химическую валентность элементов. Например, атом углерода C может объединяться с четырьмя атомами водорода H, образуя молекулу метана CH4, с двумя атомами кислорода (CO2) и т.д. Среди нуклонов нет такого разнообразия, как среди химических элементов. Поэтому насыщение ядерных сил проявляется в том, что удельная энергия связи (энергия, приходящаяся на один нуклон) в ядре при увеличении числа нуклонов в ядре не растёт, а остаётся примерно постоянной.
3. Масса ядра отличается от массы атома химического элементов лишь на величину массы электронной оболочки. В таблице Менделеева массы атомов выражаются в атомных единицах массы а.е.м. Одна а.е.м. равна 1 ç 12 массы атома углерода, 1 а.е.м. = 1,66·10-27 кг. Поскольку в ядре основного изотопа углерода 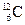 (99% на земле) 12 нуклонов, то понятно, что а.е.м. близка к массе одного нуклона.
(99% на земле) 12 нуклонов, то понятно, что а.е.м. близка к массе одного нуклона.
Масса одного электрона me = 5,5·10-4 а.е.м. Отношение массы электронной оболочки Zme к массе атома составляет у водорода me / m (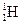 ) = 5,5·10-4 ç 1,008 = 0,0005, то есть 0,05%. У других атомов это отношение ещё меньше, поскольку число нуклонов в ядре растёт быстрее числа электронов в атоме. В атоме урана Zme / m (
) = 5,5·10-4 ç 1,008 = 0,0005, то есть 0,05%. У других атомов это отношение ещё меньше, поскольку число нуклонов в ядре растёт быстрее числа электронов в атоме. В атоме урана Zme / m (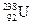 ) = 0,0002 (0,02%). Поэтому в тех случаях, когда вычисления требуют точности не более четырёх знаков, в качестве массы ядра можно брать массу атома химического элемента из таблицы Менделеева.
) = 0,0002 (0,02%). Поэтому в тех случаях, когда вычисления требуют точности не более четырёх знаков, в качестве массы ядра можно брать массу атома химического элемента из таблицы Менделеева.
По мере развития ядерной физики открывались и синтезировались посредством ядерных реакций ранее неизвестные изотопы, в том числе и не существовавшие в природе.
Химические методы измерения атомных масс искусственных изотопов оказались мало эффективными. В 1919 г. Френсис Астон конструирует массовый спектограф – прибор, способный разделять ионы по величинам их масс с высокой точностью.
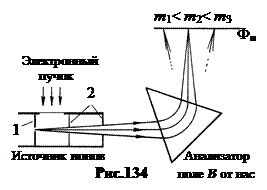 Любой масс спектограф включает в себя три основные части: ионный источник, анализатор и приёмное устройство. В ионном источнике образуются ионы и формируется слабо расходящийся пучок. В анализаторе пучок разделяется на несколько пучков, различающихся по массам ионов и фокусирующихся на поверхности приемного устройства – фотопластинки. На рис.134 показана схема одного из таких масс-спектрографов. Струя пара исследуемого элемента входит в отверстие 1 источника ионов и ионизируется простреливающим ее электронным пучком. Образующиеся ионы ускоряются и коллимируются диафрагмами 2.
Любой масс спектограф включает в себя три основные части: ионный источник, анализатор и приёмное устройство. В ионном источнике образуются ионы и формируется слабо расходящийся пучок. В анализаторе пучок разделяется на несколько пучков, различающихся по массам ионов и фокусирующихся на поверхности приемного устройства – фотопластинки. На рис.134 показана схема одного из таких масс-спектрографов. Струя пара исследуемого элемента входит в отверстие 1 источника ионов и ионизируется простреливающим ее электронным пучком. Образующиеся ионы ускоряются и коллимируются диафрагмами 2.
Анализатором служит секторное магнитное поле В, направленное перпендикулярно плоскости рисунка. В этом магнитном поле ионы, вылетающие из источника под несколько разными углами, отклоняются и фокусируются. Радиус окружности, по которой движется ион в секторе, тем больше, чем меньше его удельный заряд, 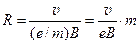 . (19.2)
. (19.2)
(См. Электричество, §14). Здесь v - скорость движения иона, e / m – его удельный заряд.
В результате ионы одного и того же изотопа попадают в одно и то же место фотопластинки Фп, образуя на ней узкую линию, перпендикулярную плоскости рисунка. Масс-спектрографы позволяют измерить массы изотопов с относительной ошибкой 10-5¸10-6.
Если заменить фотопластинку цилиндром Фарадея и измерять ионный ток, то можно определить интенсивность ионных пучков и находить относительное содержание изотопов в ионной смеси. Такой прибор называется масс-спектрометром.
4. Дефект массы и энергия связи ядра. Масса ядра m я всегда меньше масс входящих в него нуклонов Zmp + (A - Z) mn. Величина D m = Zmp + (A - Z) mn –m я (19.3)
 называется дефектом массы. Здесь mp, mn, m я – массы покоя протона, нейтрона и ядра.
называется дефектом массы. Здесь mp, mn, m я – массы покоя протона, нейтрона и ядра.
Дело в том, что при объединении свободных нуклонов выделяется энергия в виде квантов ЭМ-излучения, уносящих массу Δ m. Энергия связи E св нуклонов в ядре вычисляется по формуле E св = D mc 2, (19.4)
где c - скорость света в вакууме. Чтобы разрушить ядро, то есть разделить его на нуклоны, нужно сообщить энергию E, не меньшую энергии связи, E ≥ E св.
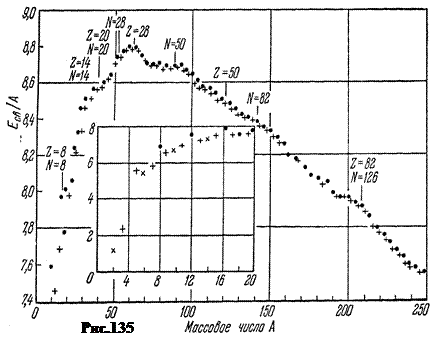
Показательна для оценки устойчивости ядер удельная энергия связи E св çA, то есть энергия, приходящаяся на 1 нуклон. На рис.135 показана опытная зависимость еёмодуля от массового числа A стабильных ядер в МэВ/нуклон. Чёрные точки относятся к чётно-чётным ядрам, у которых число протонов Z и число нейтронов A - Z – чётные числа. Прямые крестики - к ядрам с нечётным A. Косые крестики относятся к нечётно-нечётным ядрам.
На вставке показана удельная энергия связи для лёгких ядер, начиная с дейтерия (A = 2) и заканчивая неоном (A = 20).
В первом приближении удельная энергия связи изменяется в пределах от 7,4 Мэв ç нуклон у дейтерия до 8,8 Мэв ç нуклон у железа, то есть в пределах примерно 1,4 Мэв ê нуклон. Но характер изменения показателен. От дейтерия до железа велечина E св çA растёт, достигая максимума при A = 56, то есть в области ядер железа. После железа с ростом A удельная энергия связи падает до 7,5 Мэв ç нуклон в конце таблицы Менделеева.
Максимум кривой соответствует наиболее стабильным ядрам. К ним можно отнести ядра с E св çA > 8,6 Мэв ç нуклон начиная с чётно-чётного кальция 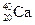 и заканчивая чётно-чётным свинцом
и заканчивая чётно-чётным свинцом 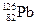 с E св çA = 7,9 Мэв ç нуклон. Легчайшим ядрам с A < 20 энергетически выгодно сливаться друг с другом в более тяжёлые с выделением термоядерной энергии. Для наиболее тяжёлых ядер с A > 207, наоборот, выгоден процесс деления на осколки, идущий с выделением энергии, которая называется атомной.
с E св çA = 7,9 Мэв ç нуклон. Легчайшим ядрам с A < 20 энергетически выгодно сливаться друг с другом в более тяжёлые с выделением термоядерной энергии. Для наиболее тяжёлых ядер с A > 207, наоборот, выгоден процесс деления на осколки, идущий с выделением энергии, которая называется атомной.
Интересно, что ядра некоторых элементов на рис.135 чуть выше хода кривой. Это ядра, в которых число протонов Z или число нейтронов N = A - Z равны так называемым магическим числам: 2, 8, 20, 28, 50, 82, 126. Эти ядра обладают повышенной по сравнению с соседями прочностью. Особенно большой прочностью отличаются дважды магические ядра 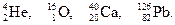 Из них ядро
Из них ядро 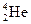 настолько прочно, что даже при распаде тяжёлых ядер вылетает целым (a -частица).
настолько прочно, что даже при распаде тяжёлых ядер вылетает целым (a -частица).
5. Спины ядер. Как уже говорилось в §18, протоны и нейтроны имеют спиновые механические моменты, такие же, как у электронов. В проекции на физическую ось спиновые механические моменты протона, нейтрона и электрона могут принимать значения Lsz = ± ћç 2.
Все методы опытного определения спиновых моментов Ls протонов, нейтронов и ядер основаны на связи механических спиновых моментов Ls с магнитными спиновыми моментами Ms. Зная соотношение между Ls и Ms для данных частиц, по величине и особенностям магнитного момента Ms можно установить механический Ls.
Самые ранние экспериментальные методы определения магнитных спиновых моментов M s были основаны на изучении сверхтонкой структуры оптических спектров водорода 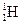 (спин протона), дейтерия
(спин протона), дейтерия 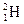 (спин ядра протон + нейтрон → спин нейтрона) и других атомов. Позднее стали изучать поведение ядер в магнитном поле методом радиоспектроскопии. Спины ядер короткоживущих изотопов определяют по ядерным реакциям на основе законов сохранения, спины возбуждённых ядер – по испускаемому ими g -излучению.
(спин ядра протон + нейтрон → спин нейтрона) и других атомов. Позднее стали изучать поведение ядер в магнитном поле методом радиоспектроскопии. Спины ядер короткоживущих изотопов определяют по ядерным реакциям на основе законов сохранения, спины возбуждённых ядер – по испускаемому ими g -излучению.
Опыты показывают, что спиновые моменты ядра (механический и магнитный, соответственно) равны геометрическим суммам моментов составляющих ядро нуклонов. При этом надо иметь в виду, что полный момент каждого нуклона является суммой спинового и орбитального (то есть связанного с движением нуклона по некой “орбите” в ядре) моментов. Орбитальный механический момент нуклона в ядре в отличие от спинового может принимать только целые значения. Если Lsz = ± ћç 2, то Llz =± nћ, где n - целое число. Перечислим основные опытные факты по ядерным спинам.
а. Спиновые механические моменты ядер с чётными A всегда целые, с нечётными A – полуцелые. Например, спин дейтрона Lsz = ± (ћç 2+ ћç 2) = ± ћ. Спины нейтрона и протона в ядре дейтерия параллельны.
б. Спиновые механические моменты всех чётно-чётных ядер в основных состояниях равны нулю. Поскольку в протон – нейтронной паре дейтерия спины параллельны, то остаётся сделать вывод, что антипараллельные спины могут быть лишь у одноимённых пар, то есть у протон-протонных и нейтрон-нейтронных.
в. Спиновые механические моменты остальных стабильных ядер не превышают 9 ћç 2, то есть очень малы по сравнению с суммой абсолютных величин спиновых и орбитальных моментов всех входящих в ядро частиц. Это говорит о том, что большинство нуклонов прочно связаны в замкнутых оболочках, имеющих нулевой суммарный момент и не участвующих в создании спина ядра.
6. Магнитные моменты ядер. Каждое ядро с ненулевым спином обладает магнитным моментом M, характеризующим взаимодействие ядра с однородным внешним магнитным полем B. Направление магнитного момента M микрочастицы совпадает с направлением спинового механического момента Ls с точностью до знака. Ms = g Ls (19.5)
Здесь g – гиромагнитное отношение. У протона оно положительно (векторы Ms и Ls совпадают, у нейтрона – отрицательно (векторы Ms и Ls противоположны). Существует много методов определения магнитных моментов ядер и нуклонов. Рассмотрим три из них.
а. Изучение сверхтонкой структуры оптических спектров. Этот метод упоминался уже в предыдущем пункте. Добавим лишь, что таким путём удалось установить, что ядерные магнитные моменты на три порядка меньше спинового магнитного момента электрона и имеют порядок ядерного магнетона Mя = eћç 2 mp = 5,05·10–27 Дж ç Тл. Поэтому сверхтонкое расщепление спектральных линий на три порядка меньше их тонкой структуры, обусловленного взаимодействием спинового момента электрона с орбитальным.
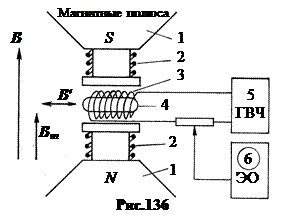 б. Метод ядерного магнитного резонанса состоит в том, что спин ядра, находящегося в сильном постоянном магнитном поле, может “опрокидываться” под действием слабого высокочастотного поля некоторой резонансной частоты. Схема установки показана на рис.136.
б. Метод ядерного магнитного резонанса состоит в том, что спин ядра, находящегося в сильном постоянном магнитном поле, может “опрокидываться” под действием слабого высокочастотного поля некоторой резонансной частоты. Схема установки показана на рис.136.
 На ядра исследуемого образца, находящегося в ампуле 4, действуют три магнитных поля. Во-первых, сильное постоянное магнитное поле B ≈ 1 Тл, создаваемое магнитами 1. Назначение магнитного поля B – разрыв связи ядерного магнитного момента с электронной оболочкой, создание сверхтонкого Зеемановского расщепления уровней ядра. Во-вторых, создаваемое катушкой 3 от генератора 5 высокочастотное поле B ', направленное перпендикулярно B. Частота поля B ' может изменяться. Назначение этого поля – резонансное опрокидывания спина ядра. В-третьих, создаваемое катушками 2 модулирующее переменное поле B m, направленное параллельно B и имеющее низкую постоянную частоту 50 Гц. Назначение этого поля – повторять опрокидывание спина ядра 50 раз в секунду для того, чтобы в резонансе получить на осциллографе 6 стационарную картинку. Измеряя поглощаемую в резонансе образцом энергию, индукцию сильного магнитного поля B и частоту генератора, можно определить магнитный момент ядер на современных установках с точностью до 6 знаков.
На ядра исследуемого образца, находящегося в ампуле 4, действуют три магнитных поля. Во-первых, сильное постоянное магнитное поле B ≈ 1 Тл, создаваемое магнитами 1. Назначение магнитного поля B – разрыв связи ядерного магнитного момента с электронной оболочкой, создание сверхтонкого Зеемановского расщепления уровней ядра. Во-вторых, создаваемое катушкой 3 от генератора 5 высокочастотное поле B ', направленное перпендикулярно B. Частота поля B ' может изменяться. Назначение этого поля – резонансное опрокидывания спина ядра. В-третьих, создаваемое катушками 2 модулирующее переменное поле B m, направленное параллельно B и имеющее низкую постоянную частоту 50 Гц. Назначение этого поля – повторять опрокидывание спина ядра 50 раз в секунду для того, чтобы в резонансе получить на осциллографе 6 стационарную картинку. Измеряя поглощаемую в резонансе образцом энергию, индукцию сильного магнитного поля B и частоту генератора, можно определить магнитный момент ядер на современных установках с точностью до 6 знаков.
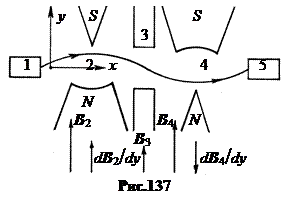
в. Метод Исидора Раби, 1937 г. Методом ядерного магнитного резонанса нельзя измерить магнитный момент нейтрона, поскольку нейтроны не удерживаются в ампуле, они существуют только в пучках. Схема метода Раби показана на рис.137. Пучок нейтронов из источника 1 последовательно проходит через два сильно неоднородных магнитных поля 2 и 4 с противоположно направленными градиентами dBçdy. В неоднородном магнитном поле траектория частицы, имеющей спиновый магнитный момент, искривляется по градиенту или против него в зависимости от ориентации магнитного момента. Первое магнитное поле 2 искривляет траекторию нейтронов, второе поле 4 фокусирует их на детектор 5. Если теперь в промежутке 3 между полями включить из предыдущей схемы комбинацию постоянного сильного однородного и слабого высокочастотного магнитных полей, то в резонансе спин нейтронов будет опрокидываться. В результате эти нейтроны не сфокусируются вторым неоднородным полем 4 и не попадут в детектор 5. Поэтому на графике интенсивности счета в детекторе в зависимости от частоты высокочастотного поля в резонансе будет резкий провал. Его положение и определит величину магнитного момента нейтрона.
В методе Раби могут использоваться так же молекулярные пучки и определяться магнитные моменты ядер.
Перечислим основные опытные факты по магнитным моментам нуклонов и атомных ядер.
а. Магнитные спиновые моменты протона Mp и нейтрона Mn составляют: Mp = 2,79 Mя, Mn = –1,91 Mя. Здесь Mя = ehç 2 mp = 5,05·10–27 Дж ç Тл – ядерный магнетон.
б. Магнитные моменты ядер с нулевым спином равны нулю.
в. Магнитные моменты ядер с ненулевым спином имеют порядок ядерного магнетона.
г. Спиновые магнитные моменты нуклонов не аддитивны. Например, дейтрон состоит из протона и нейтрона с параллельными спинами. Суммарный магнитный момент дейтрона должен быть Md = Mp + Mn = 2,79 Mя – 1,91 Mя = 0,88 Mя. Но опыт даёт Md = 0,86 Mя. Эта неаддитивность связана с нецентральностью сил, действующих мужду нуклонами.
7. Модели атомного ядра. Последовательная теория ядра не построена до сих пор из-за двух основных трудностей: недостаточного знания о силах, действующих между нуклонами, и громоздкости квантовой задачи многих тел. Ведь ядро с массовым числом A должно описываться системой, состоящей не менее чем из A уравнений. Эти трудности удаётся частично преодолеть путём создания ядерных моделей, позволяющих описывать с помощью простых уравнений некоторую совокупность свойств ядра.
Разработано около десятка моделей, каждая из которых описывает свою совокупность свойств ядра и свой круг явлений. Рассмотрим две из них.
а. Капельная модель. Её предложил Яков Френкель в 1937 г. Ядро в этой модели уподобляется капле жидкости, возбуждённое ядро - нагретой капле. Если E – энергия возбуждённого ядра с числом нуклонов A, то, приписав нуклонам 3 степени свободы, получаем:
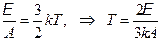 . (19.6)
. (19.6)
При E = 10 МэВ T ≈ 109 K. Испускание нейтронов, протонов и a -частиц в такой модели можно трактовать как испарение ядра капли.
Основанием для капельной модели послужило короткодействие ядерных сил и независимость плотности от массового числа A. Капельная модель позволила вывести полуэмпирическую формулу для энергии связи частиц в ядре и описать процесс деления тяжёлых ядер.
б. Оболочечная модель. Её предложила в 1951 г. Мария Гепперт-Майер. Основанием для оболочечной модели послужил факт существования особо устойчивых ядер, так называемых магических и дважды магических.
В этой модели нуклоны считаются движущимися независимо друг от друга в усреднённом центрально-симметричном поле. Полагается, что как и в атоме, в ядре имеются дискретные уровни, заполняемые нуклонами с учётом принципа Паули. Эти уровни группируются в оболочки, в каждой из которой может находиьтся определённое число нуклонов. Полностью заполненная оболочка образует устойчивое ядро.
Из опытного факта существования магических и дважды магических ядер следует, что заполненные оболочки содержат магическое число нуклонов 2, 8, 20, 28, 50, 82, 126. Многие магические ядра более распространены во Вселенной, чем их немагические соседи. Кроме дважды магических 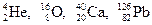 (за исключением
(за исключением 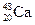 ) сюда относятся
) сюда относятся 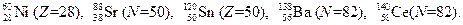
Оболочная модель хорошо разработана математически и позволяет объяснить свойства магических ядер и ядер-соседей, отличающихся на 1 нуклон (недостающий или избыточный). В этой модели реальные силы, действующий между нуклонами, заменяются самосогласованным полем, в котором независимо друг от друга движутся нуклоны. Схема выстраивания оболочек чем-то напоминает заполнение таблицы Менделеева, но уступает ей по строгости.
 2014-02-02
2014-02-02 2875
2875
