Для определения положения точек в геодезии применяют пространственные прямоугольные, геодезические и плоские прямоугольные координаты.
Пространственные прямоугольные координаты. Начало системы координат расположено в центре O земного эллипсоида (рис. 2.2).
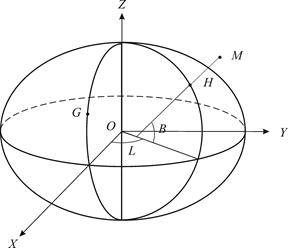 | Рис. 2.2. Земной эллипсоид и координаты: Х, Y, Z – пространственные прямоугольные; B, L, H - геодезические; G - Гринвич |
Ось Z направлена по оси вращения эллипсоида к северу. Ось Х лежит в пересечении плоскости экватора с начальным - гринвичским меридианом. Ось Y направлена перпендикулярно осям Z и X на восток.
Геодезические координаты. Геодезическими координатами точки являются ее широта, долгота и высота (рис. 2.2).
Геодезической широтой точки М называется угол В, образованный нормалью к поверхности эллипсоида, проходящей через данную точку, и плоскостью экватора.
Широта отсчитывается от экватора к северу и югу от 0° до 90° и называется северной или южной. Северную широту считают положительной, а южную - отрицательной.
Плоскости сечения эллипсоида, проходящие через ось OZ, называются геодезическими меридианами.
Геодезической долготой точки М называется двугранный угол L, образованный плоскостями начального (гринвичского) геодезического меридиана и геодезического меридиана данной точки.
Долготы отсчитывают от начального меридиана в пределах от 0° до 360° на восток, или от 0° до 180° на восток (положительные) и от 0° до 180° на запад (отрицательные).
Геодезической высотой точки М является ее высота Н над поверхностью земного эллипсоида.
Геодезические координаты с пространственными прямоугольными координатами связаны формулами
X = (N + H)cos B cos L,
Y = (N+H)cos B sin L,
Z = [(1 - e2) N+H ] sin B,
где e - первый эксцентриситет меридианного эллипса и N -радиус кривизны первого вертикала.При этом N=a/ (1 - e 2 sin2 B)1/2.
Геодезические и пространственные прямоугольные координаты точек определяют с помощью спутниковых измерений, а также путем их привязки геодезическими измерениями к точкам с известными координатами.
Отметим, что наряду с геодезическими существуют еще астрономические широта и долгота. Астрономическая широта j это - угол, составленный отвесной линией в данной точке с плоскостью экватора. Астрономическая долгота l – угол между плоскостями Гринвичского меридиана и проходящего через отвесную линию в данной точке астрономического меридиана. Астрономические координаты определяют на местности из астрономических наблюдений.
Астрономические координаты отличаются от геодезических потому, что направления отвесных линий не совпадают с направлениями нормалей к поверхности эллипсоида. Угол между направлением нормали к поверхности эллипсоида и отвесной линией в данной точке земной поверхности называется уклонением отвесной линии.
Обобщением геодезических и астрономических координат является термин – географические координаты.
Плоские прямоугольные координаты. Для решения задач инженерной геодезии от пространственных и геодезических координат переходят к более простым – плоским координатам, позволяющим изображать местность на плоскости и определять положение точек двумя координатами х и у.
Поскольку выпуклую поверхность Земли изобразить на плоскости без искажений нельзя, введение плоских координат возможно только на ограниченных участках, где искажения так малы, что ими можно пренебречь. В России принята система прямоугольных координат, основой которой является равноугольная поперечно–цилиндрическая проекция Гаусса. Поверхность эллипсоида изображается на плоскости по частям, называемым зонами. Зоны представляют собой сферические двуугольники, ограниченные меридианами, и простирающиеся от северного полюса до южного (рис. 2.3). Размер зоны по долготе равен 6°. Центральный меридиан каждой зоны называется осевым. Нумерация зон идет от Гринвича к востоку.
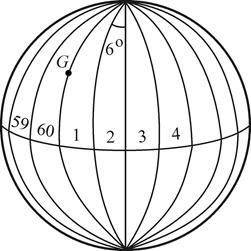 | Рис. 2.3. Деление поверхности Земли на координатные зоны: G – Гринвич |
Долгота осевого меридиана зоны с номером N равна:
l0 = 6°× N - 3°.
Осевой меридиан зоны и экватор изображаются на плоскости прямыми линиями (рис. 2.4). Осевой меридиан принимают за ось абсцисс x, а экватор - за ось ординат y. Их пересечение (точка O) служит началом координат данной зоны.
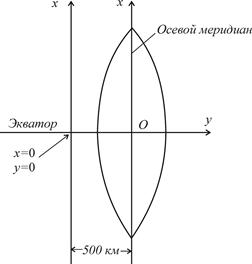 | Рис. 2.4. Изображение координатной зоны на плоскости: О – начало координат (х 0=0; у 0=500 км). |
Чтобы избежать отрицательных значений ординат, координаты пересечения принимают равными x 0 = 0, y 0 = 500 км, что равносильно смещению оси х к западу на 500 км.
Чтобы по прямоугольным координатам точки можно было судить, в какой зоне она расположена, к ординате y слева приписывают номер координатной зоны.
Пусть например, координаты точки А имеют вид:
xА = 6 276 427 м
yА = 12 428 566 м
Эти координаты указывают на то, что точка А находится на расстоянии 6276427 м от экватора, в западной части (y < 500 км) 12-ой координатной зоны, на расстоянии 500000 - 428566 = 71434 м от осевого меридиана.
Для пространственных прямоугольных, геодезических и плоских прямоугольных координат в России принята единая система координат СК-95, закрепленная на местности пунктами государственной геодезической сети и построенная по спутниковым и наземным измерениям по состоянию на эпоху 1995 г.
Местные системы прямоугольных координат. При строительстве различных объектовчасто используют местные (условные) системы координат, в которых направления осей и начало координат назначают, исходя из удобства их использования в ходе строительства и последующей эксплуатации объекта.
Так, при съемке железнодорожной станции ось у направляют по оси главного железнодорожного пути в направлении возрастания пикетажа, а ось х – по оси здания пассажирского вокзала.
При строительстве мостовых переходов ось х обычно совмещают с осью моста, а ось y идет в перпендикулярном направлении.
При строительстве крупных промышленных и гражданских объектов оси x и y направляют параллельно осям строящихся зданий.
 2014-02-02
2014-02-02 25203
25203
