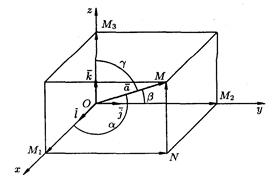
Системой прямоугольных (декартовых координат) называется совокупность точки O и базиса, обозначаемого 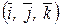 и удовлетворяющего условиям:
и удовлетворяющего условиям:
1) 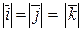 =1;
=1;
2) 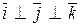 ,
,
3) тройка векторов 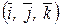 - правая.
- правая.
Любой вектор  можно представить в виде разложения по базису
можно представить в виде разложения по базису
 |
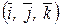 :
:
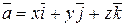 ,
,
числа х, у, z называются прямоугольными ( декартовыми ) координатами вектора  .
.
Геометрический смысл координат вектора – координаты вектора есть проекции этого вектора на координатные оси:
х= 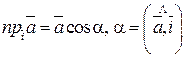 ;
;
у= 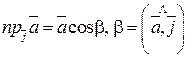 ;
;
z= 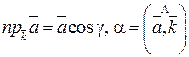 .
.
Cos a, cos b, cos g - называются направляющими косинусами вектора.
Пусть даны точка М1 (х1,у1,z1) и точка М2 (х2,у2,z2), тогда вектор 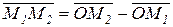 .
.
Координаты вектора 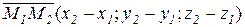 .
.
Модуль вектора 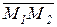 , равный расстоянию между точками М1 и М2, находится по формуле:
, равный расстоянию между точками М1 и М2, находится по формуле:
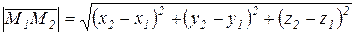 .
.
Рассмотрим векторы  (ха; уа; zа) и
(ха; уа; zа) и  (хb; уb; zb), тогда
(хb; уb; zb), тогда
- если 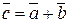 , то
, то 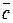 (ха+хb; уа+уb; zа+zb);
(ха+хb; уа+уb; zа+zb);
- если 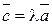 , то
, то 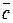 (l ха; l уа; l zа).
(l ха; l уа; l zа).
Условие коллинеарности векторов в координатной форме:
векторы  и
и  коллинеарны (
коллинеарны ( =l
=l  ) тогда и только тогда, когда
) тогда и только тогда, когда
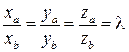 .
.
Координаты середины отрезка М1М2:
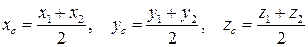 .
.
2.7. Скалярное произведение векторов
Скалярным произведением двух векторов называется число, равное произведению модулей этих векторов на косинус угла между ними:
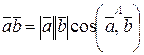 .
.
Алгебраические свойства скалярного произведения:
1) 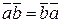 - свойство коммутативности;
- свойство коммутативности;
2) 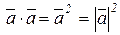 - скалярное произведение вектора на себя равно квадрату модуля вектора;
- скалярное произведение вектора на себя равно квадрату модуля вектора;
3) ( a  )= a (
)= a ( ) – свойство ассоциативности;
) – свойство ассоциативности;
4) ( +
+  )
) 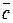 =
= 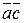 +
+ 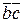 - свойство дистрибутивности.
- свойство дистрибутивности.
Геометрические свойства скалярного произведения:
1) 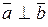 тогда и только тогда, когда
тогда и только тогда, когда 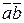 = 0 – условие ортогональности векторов;
= 0 – условие ортогональности векторов;
2) Два ненулевых вектора  и
и  составляют:
составляют:
- острый угол, если 
 >0;
>0;
- тупой угол, если 
 <0;
<0;
Скалярное произведение в координатах двух векторов  (ха; уа; zа) и
(ха; уа; zа) и  (хb; уb; zb) есть число, равное сумме произведений одноименных координат:
(хb; уb; zb) есть число, равное сумме произведений одноименных координат:
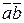 = xaxb+yayb+zazb.
= xaxb+yayb+zazb.
Из определения скалярного произведения вытекают следующие формулы:
- косинус угла между векторами 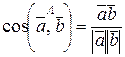 ;
;
- проекция вектора  на вектор
на вектор  равна
равна 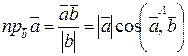 .
.
 2015-10-16
2015-10-16 2086
2086
