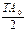Лекция 14 расчёт размерных цепей методом максимума и минимума. Основные зависимости. Пример решения

В предыдущей лекции мы рассмотрели основные идеи метода максимума и отметили, что в соответствии с данным методом величины составляющих звеньев в пределах их допусков могут принимать любые значения, в том числе и предельные.

Метод максимума и минимума обеспечивает полную взаимозаменяемость.

Рассмотрим основные соотношения метода максимума и минимума при решении обратной задачи.

Пусть размерная цепь содержит m – звеньев из которых n – увеличивающих звеньев и р – уменьшающих.

Номинальный размер замыкающего звена линейной размерной цепи определяется формулой

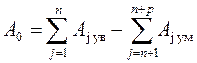Допуск замыкающего звена равен сумме допусков составляющих звеньев

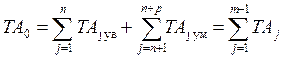Наибольшее и наименьшее предельные отклонения замыкающего звена определяются по формулам:

;

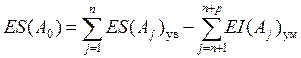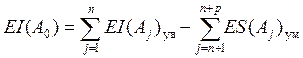Координата середины поля допуска замыкающего звена определяется по формуле

Предельные отклонения замыкающего звена связаны с координатой середины поля допуска замыкающего звена соотношениями

ТA₀

ES(A₀)

0 0

EI(A₀)

E_С(A₀)

;

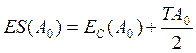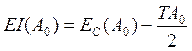На основе приведенных формул можно сделать некоторые выводы:

1. Чем больше количество составляющих звеньев, тем больше допуск замыкающего звена.

2. Чем больше допуски составляющих звеньев, тем больше допуск замыкающего звена.

3. Чтобы обеспечить наименьшую погрешность замыкающего звена нужно соблюдать принцип кратчайшей цепи с возможно меньшим числом звеньев.

4. Порядок обработки и сборки деталей надо строить так, чтобы замыкающим был менее ответственный размер, т.к. его погрешность будет наибольшей.

Рассмотрим пример.

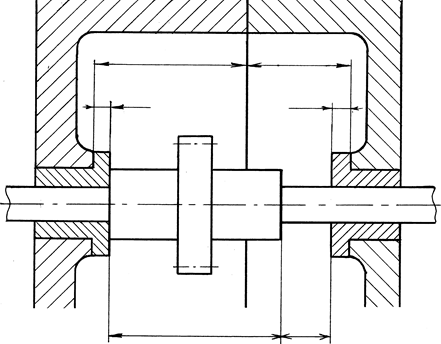
А₁ А₂

А₃ А₅

А₁ А₂

А₀

А₃ А₄ А₅

А₄ А₀

А₁ = 101^+0,14; А₂ = 50^+0,1; А₃ = А₅ = 5_-0,03; А₄ = 140_-0,1.

Величина замыкающего звена (номинальный размер) равна

А₀ = (101+50) – (5+140+50) = 1 мм.

Допуски составляющих звеньев

ТА_j = ЕS(А_j) – ЕI(А_j);

ТА₁ = 0,14 – 0 = 0,14; ТА₂ = 0,1 – 0 = 0,1;

ТА₃ = ТА₅ = 0 – (-0,03) = 0,03; ТА₄ = 0–(-0,1)=0,1.

Допуск замыкающего звена

ТА₀ = 0,14+0,1+0,03+0,03+0,1 = 0,4 мм.

Предельные отклонения замыкающего звена

ЕS(А₀) = 0,14+0,1 – (-0,03) – (-0,03) – (-0,1) = 0,4 мм.

ЕI(А₀) = 0 + 0 – 0 – 0 – 0 = 0.

А₀ = 1^+0,4; ТА₀ = 0,4 – 0 = 0,4 мм.

Как видно из результатов расчёта, допуск замыкающего звена получился наибольший по сравнению с допусками составляющих звеньев.

Предельные размеры замыкающего звена:

А_{0 max} = А₀ + ES(A₀) = 1 + 0,4 = 1,4 мм;

А_{0 min} = А₀ + EI(A₀) = 1 + 0= 1 мм.

Решение прямой задачи по методу максимума и минимума.

Прямая задача в конструкторской практике встречается наиболее часто. Основная цель при этом – назначить допуски на составляющие звенья так, чтобы обеспечить заданную точность исходного размера.

Прямая задача по методу max и min решается двумя способами:

- способ равных допусков;

- способ допусков одного квалитета.

Способ равных допусков применяют, если размеры звеньев, составляющих размерную цепь, являются величинами одного порядка, например, входят в один интервал и могут быть выполнены с примерно одинаковой экономической точностью.

В этом случае можно принять

ТА₁ = ТА₂ = … = ТА_j т.е. ТА₀ = (m – 1) · ТА_j, откуда ,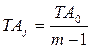

где m – общее количество звеньев размерной цепи, включая и исходное звено.

Полученный средний допуск корректирует в зависимости от величина составляющих размеров так, чтобы соблюдалось правило:

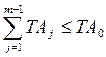т.е. чтобы сумма допусков составляющих звеньев не превышала допуск исходного звена.

Способ равных допусков прост, но имеет ограниченную область применения.

Способ допусков одного квалитета.

При использовании данного способа предполагают, что по известному допуску исходного звена допуски на остальные звенья могут быть назначены по одному квалитету с учётом величин этих звеньев.

Требуемый квалитет определяют следующим образом.

Как вы помните, допуск любого размера в интервале 1…500 мм определяется формулой

Т = а · i.

Т.к. мы приняли, что на составляющие звенья будем назначать допуски по одному квалитету, то количество единиц допуска а будет для всех звеньев одно и тоже.

А единица допуска i будет для каждого размера своя, в зависимости от того, в какой интервал попадёт этот размер.

Как вы помните .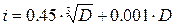

Запишем условие равенства допуска исходного звена сумме допусков остальных звеньев.

ТА₀ = а·i₁+ а·i₂+ … + а·i_j + … + а·i_{m – 1};

т.е. ,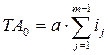

Откуда .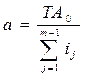

Полученное количество единиц допуска округляем до ближайшего стандартного и по нему в соответствии с СТ СЭВ 145-75 определяем квалитет.

По известному квалитету и номинальным размерам составляющих звеньев определяем их допуски.

Рекомендуется для охватывающих размеров допуски определять как для основного отверстия, а для охватываемых – как для основного вала.

Затем производится проверка на соблюдение условия.

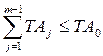Если это условие не соблюдается, на одно из звеньев размерной цепи допуск назначают по более точному квалитету.

Пример. Рассмотрим туже размерную цепь, но для решения прямой задачи методом допусков одного квалитета. Пусть заданы номинальные размеры всех звеньев и допуск исходного звена А₀.

А₁ А₂

А₀

А₃ А₄ А₅

А₁ = 101; А₂ = 50; А₃ = А₅ = 5; А₄ = 140; А₀ = 1^+0,75.

Допуск исходного звена

ТА₀ = ES – EI = 0,75 – 0 = 0,75 = 750 мкм.

Определим число единиц допуска

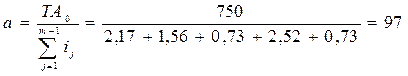По СТ СЭВ 145-75 10 ^му квалитету соответствует а=64, а 11 ^му а=100.

Принимаем а = 100, т.е. 11 ^й квалитет и определяем по таблицам допуски для составляющих звеньев.

ТА₁ = 0,22; ТА₂ = 0,16; ТА₃ = ТА₅ = 0,075; ТА₄ = 0,25 мм.

Проверяем условие равенства допуска исходного звена сумме допусков составляющих звеньев.

0,22 + 0,16 + 0,075 + 0,075 + 0,25 = 0,78 > 0,75,

т.е. условие не соблюдается.

На четвёртое звено назначаем допуск не по 11 ^му, а по 10 ^му квалитету ТА₄ = 0,16 мм.

При этом условие соблюдается

0,22 + 0,16 + 0,075 + 0,075 + 0,16 = 0,69 < 0,75.

В соответствии с рекомендациями по полученным допускам назначаем отклонения с учётом того, что размеры А₁ и А₂ – охватывающие, а А₃, А₄, А₅ – охватываемые.

А₁ = 101^+0,22; А₂ = 50^+0,16; А₃ = А₅ = 5_-0,075; А₄ = 140_-0,16.