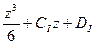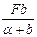Перемещения при изгибе.
При изгибе ось балки искривляется, а поперечные сечения перемещаются поступательно и поворачиваются вокруг нейтральных осей, оставаясь при этом перпендикулярными к изогнутой продольной оси (рис.6.23). Деформированная ось балки называется упругой линией, а поступательные перемещения сечений, равные перемещениям у(z) их центров тяжести сечений – прогибами балки. Прогибы у(z) и углы поворота сечений θ(z) связаны между собой. Из рис.6.22 видно, что угол поворота сечения θ равен углу φ наклона касательной к упругой линии, так как это углы с взаимно перпендикулярными сторонами. Согласно геометрическому смыслу первой производной у' =tgφ. Таким образом, tg θ = tgφ = у'.
В пределах упругих деформаций прогибы балок малы, а углы поворота не превышают 0,1рад, поэтому можно принять θ= у'.
Форма упругой линии балки определяется выражения кривизны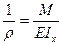 (α), полученной при выводе формулы нормальных напряжений.
(α), полученной при выводе формулы нормальных напряжений.
|
|

дифференциальное уравнение упругой линии балки 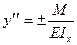 . (6.14)
. (6.14)
Выбор знака в правой части этого уравнения определяется направлением оси У, так как от этого направления зависит знак второй производной
При ЕIх=const, М=М(z) 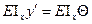 =
=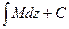 ,
,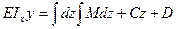 .
.
Постоянные интегрирования C и D определяются из граничных условий.
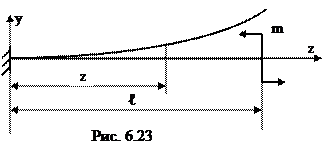
|
EI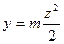 .
.
Полученное уравнение прогибов представляет квадратичную параболу, но по выра-жению 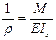 =
=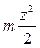 = const балка должна изогнуться по дуге окружности. В полученных результатах наглядно проявляется приближенный характер уравнения
= const балка должна изогнуться по дуге окружности. В полученных результатах наглядно проявляется приближенный характер уравнения 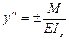 . Однако, в пределах длины балки ℓ указанные дуги параболы и окружности практически совпадают.
. Однако, в пределах длины балки ℓ указанные дуги параболы и окружности практически совпадают.
Если балка имеет несколько участков с различными аналитическими выражениями из-гибающих моментов, то дифференциальные уравнения упругой линии также будут различны. Интегрирование таких уравнений для n участков приводит к 2 n постоянных интегрирования. Для их определения к граничным условиям на опорах добавляются условия равенства проги-бов и углов поворота сечений на стыке смежных участков. Рассмотрим это на примере балки с двумя участками (рис.6.24).
I участок: 0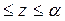 : EIx
: EIx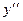 =
=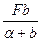 z,
z,
|
|
|
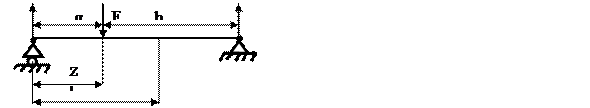
Рис.6.24
I I участок: α 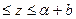 EIx
EIx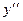 =
=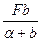 z – F(z-α),
z – F(z-α),
EIx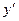 =
=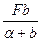
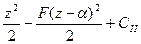 ,
,
EIx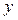 =
=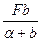
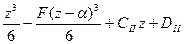 .
.
Здесь интегрирование идет без раскрытия скобок, т.е., переменной интегрирования является (z – α) а не z, что скажется только на величинах СI I , DI I
Граничные условия: 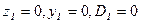 ;
;
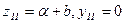 ,
, 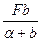
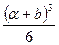
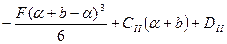 =0,
=0,
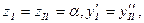
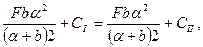



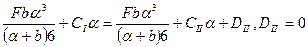 ,
,
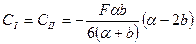 .
.
 2014-02-02
2014-02-02 8766
8766

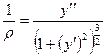 . (b)
. (b) 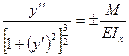 . Полученное уравнение называется
. Полученное уравнение называется 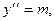 EI
EI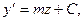 EI
EI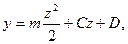 Из граничных условий при z = 0 следует:
Из граничных условий при z = 0 следует: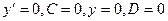 ,
, 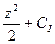 EIx
EIx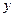 =
=