Балки переменного сечения и балки равного сопротивления

По конструктивным или иным причинам часто приходится выполнять балку с пере-менным сечением.

Формулы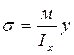, , 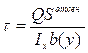,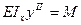полученные для балок с постоянным сечением на основании гипотезы плоских сечений, становятся неверными (как и сама гипот-еза). Однако, методами теории упругости показано, что если угол наклона образующей повер-хности стержня к его оси не превышает 15-20 градусов, то с достаточной для практики точ-ностью можно пользоваться обычным условием прочности 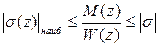. Формула Журавского в этом случае дает значительные погрешности.

Частным случаем балок с непрерывно изменяющимися размерами сечения по её длине являются балки равного сопротивления изгибу.

Балкой равного сопротивления называется балка, у которой во всех сечениях максимальное напряжение равно допускаемому: .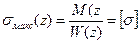

Отсюда получается уравнение для определения размеров балки равного сопротивления:

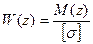(6.15)

Задавшись какой-либо формой сечения, размеры которого будут определяться только одним параметром, из уравнения (6.15) можно определить закон изменения этого параметра по длине балки.

Найдём закон изменения поперечного сечения балки равного сопротивления, изображённой на рис.6.25

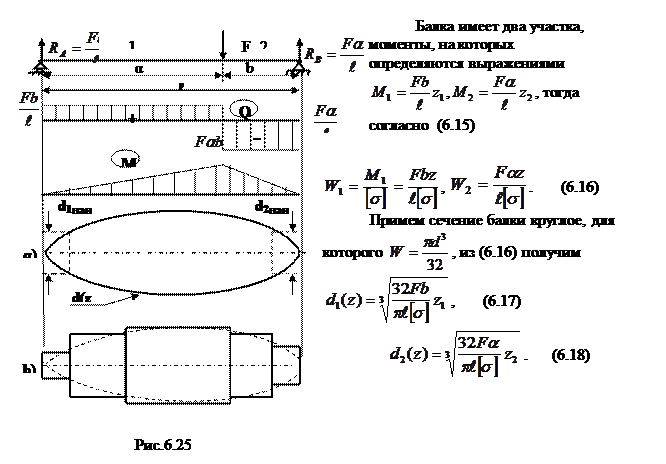
Возле опор напряжения в балке малы, а потому размеры сечения будут определяться касательными напряжениями: 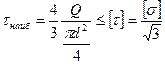. (6.19)

Подставляя в (6.17) значения Q для каждого участка, получим значения диаметров балки на её концах (6.25 α): ,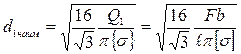

.

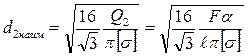Переход к балке равного сопротивления позволяет уменьшить её массу и увеличить податливость, т.е., при тех же силах увеличатся её прогибы, что ей позволяет воспринимать безопасно большие энергии. Поэтому балка равного сопротивления лучше сопротивляется ударным нагрузкам.

Согласно (6.17), (6.18) рассмотренная балка будет иметь параболические очертания. Изготовление такой балки связано с большими технологическим трудностями, поэтому на практике применяют не балки равного сопротивления, а близкие к ним ступенчатые балки

(6.25 b)

Примером балки равного сопротивления может служить автомобильная рессора, масса которой в два раза меньше, а податливость в 1,2-1,4 раза больше в сравнении с балкой постоянного сечения.