С учетом величины Fкр критические напряжения определятся выражением
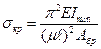 . Так как
. Так как 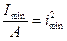 , то
, то 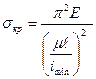
Выражение 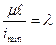 называется гибкостью стержня, тогда
называется гибкостью стержня, тогда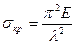 .
.
Формула Эйлера была выведена с использованием дифференциального уравнения изогнутой оси балки, которое справедливо в пределах упругих деформаций, поэтому критические напряжения не могут превышать предела пропорциональности, т.е.
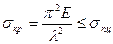 .
.
Из этого равенства определится гибкость стержня, соответствующая пределу пропорциональности
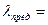
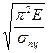 (8.4).
(8.4).
Таким образом, формула Эйлера для определения критической силы может быть использована для стержней большой гибкости, когда 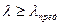 .
.
Критические напряжения в стержнях средней гибкости при 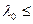
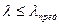 определяются по формуле Ясинского
определяются по формуле Ясинского 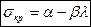 . Здесь λ0 - предельное значение гибкости стержня, при которой потеря устойчивости не наблюдается. Величины α, β, λ0, и λпред являются параметрами, зависящими от механических свойств материала. Например, для ст. 2, у которой
. Здесь λ0 - предельное значение гибкости стержня, при которой потеря устойчивости не наблюдается. Величины α, β, λ0, и λпред являются параметрами, зависящими от механических свойств материала. Например, для ст. 2, у которой 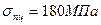 ,
, 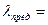
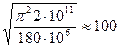 , λ0 =62, α =264 МПа, β=0,7 МПа. Стержни малой гибкости не теряют устойчивости (λ0 ≥λ), они разрушаются при достижении напряжениями предельных величин.
, λ0 =62, α =264 МПа, β=0,7 МПа. Стержни малой гибкости не теряют устойчивости (λ0 ≥λ), они разрушаются при достижении напряжениями предельных величин.
Полный график критических напряжений представлен на рисунке
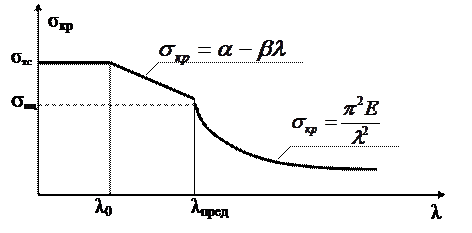 |
 2014-02-02
2014-02-02 2805
2805








