2014-02-02
971
Лекция N 4
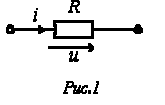1. Резистор
Идеальный резистивный элемент не обладает ни индуктивностью, ни емкостью. Если к нему приложить синусоидальное напряжение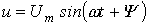 
(см. рис. 1), то ток i через него будет равен
 .
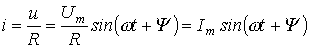| (1) |
Соотношение (1) показывает, что ток имеет ту же начальную фазу, что и напряжение. Таким образом, если на входе двухлучевого осциллографа подать сигналы u и i, то соответствующие им синусоиды на его экране будут проходить (см. рис. 2) через нуль одновременно, т.е. на резисторе напряжение и ток совпадают по фазе.
Из (1) вытекает:
;
.
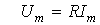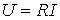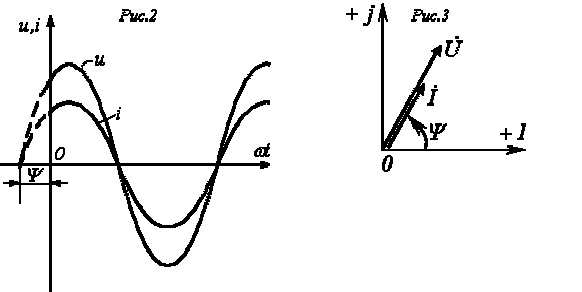
Переходя от синусоидальных функций напряжения и тока к соответствующим им комплексам:
;
,
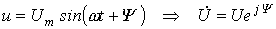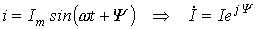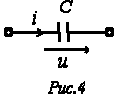- разделим первый из них на второй:
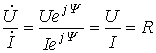
или
 .
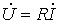| (2) |
Полученный результат показывает, что отношение двух комплексов есть вещественная константа. Следовательно, соответствующие им векторы напряжения и тока (см. рис. 3) совпадают по направлению.
2. Конденсатор
Идеальный емкостный элемент не обладает ни активным сопротивлением (проводимостью), ни индуктивностью. Если к нему приложить синусоидальное напряжение 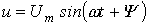(см. рис. 4), то ток i через него будет равен
|
|
|
 .
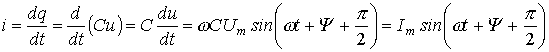| (3) |
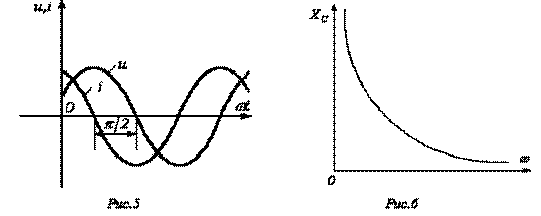
Полученный результат показывает, что напряжение на конденсаторе отстает по фазе от тока на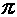 
/2. Таким образом, если на входы двухлучевого осциллографа подать сигналы u и i, то на его экране будет иметь место картинка, соответствующая рис. 5.
Из (3) вытекает:
;
.
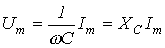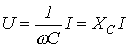Введенный параметр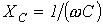 
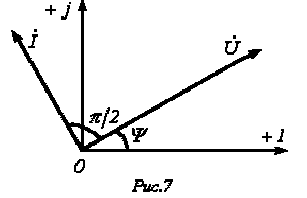
называют реактивным емкостным сопротивлением конденсатора. Как и резистивное сопротивление,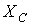 
имеет размерность Ом. Однако в отличие от R данный параметр является функцией частоты, что иллюстрирует рис. 6. Из рис. 6 вытекает, что при 
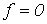конденсатор представляет разрыв для тока, а при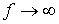 
.
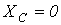Переходя от синусоидальных функций напряжения и тока к соответствующим им комплексам:
;
,
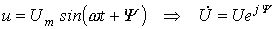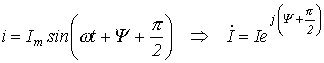- разделим первый из них на второй:
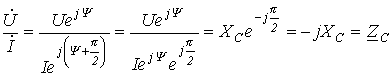
или
 .
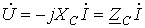| (4) |
В последнем соотношении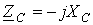 
- комплексное сопротивление конденсатора. Умножение на 
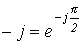соответствует повороту вектора на угол 
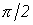по часовой стрелке. Следовательно, уравнению (4) соответствует векторная диаграмма, представленная на рис. 7.
