Режим двигателя
Рассмотрим два крайних режима двигателя:
а) холостой ход двигателя
При холостом ходе нет нагрузки на валу, ротор под действием вращающего магнитного поля статора разгонится до скорости близкой к синхронной, а ток статора равен току холостого хода. Мощность, потребляемая из сети пойдет на покрытие потерь, т.е.
Ро = Рэл1 + Рмг + Рмех + Рдоб
Разница между трансформатором и двигателем будет только конструктивная. В двигателе имеется воздушный зазор. Поэтому ток холостого хода двигателя равен 20 ¸ 30% от номинального.
б) режим короткого замыкания
При этом режиме ротор механически заторможен, а обмотка ротора закорочена. К статору подводится пониженное напряжение, при котором ток имеет значение близкое к номинальному. Мощность короткого замыкания пойдет на покрытие потерь в стали и обмотках. При номинальном напряжении пусковой ток
Iп = (5 ¸ 7)Iн.
Используя данные режима холостого хода и короткого замыкания можно построить круговую диаграмму, а по ней определить рабочие характеристики двигателя при нагрузке.
При рассмотрении этого вопроса увидим что частота ротора, ЭДС и индуктивное сопротивление с изменением скорости вращения ротора не остаются постоянными. Запишем выражение ЭДС неподвижного ротора.
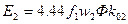
ЭДС для вращающегося ротора

где f2 – частота ЭДС ротора
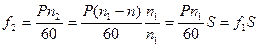
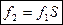
тогда E2s=4.44f1 w2 Ф k02 S = E2 S
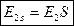
т.е. ЭДС для вращающего ротора равна ЭДС неподвижного ротора умноженной на скольжение.
Индуктивное сопротивление неподвижного ротора
X2=2 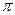 f1 L2, где L2 – индуктивность фазы ротора
f1 L2, где L2 – индуктивность фазы ротора
Индуктивное сопротивление вращающего ротора
X2=2 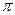 f2 L2 =2
f2 L2 =2 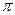 f1 L2S =X2S
f1 L2S =X2S

т.е. индуктивное сопротивление вращающего ротора равно индуктивному сопротивлению неподвижного ротора умноженное на скольжение. Таким образом видим, что частота, ЭДС и индуктивное сопротивление ротора зависят от скольжения. Теперь можно записать выражение для тока ротора 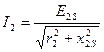 . Ток ротора будет создавать магнитное поле.
. Ток ротора будет создавать магнитное поле.
Из законов электромеханики следует, что передача энергии от одного звена к другому, для любой электрической машины, возможна лишь тогда, когда магнитные поля вращаются с одинаковой скоростью.
Докажем это для асинхронного двигателя:
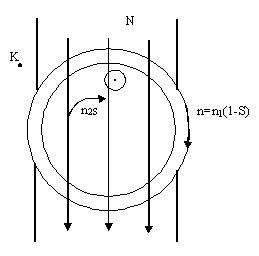 1. Определим скорость магнитного потока созданного током ротора I2 относительно ротора
1. Определим скорость магнитного потока созданного током ротора I2 относительно ротора
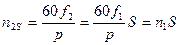
2. Определим скорость магнитного поля ротора относительно неподвижного статора (точка К)
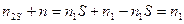 , рис. 107.
, рис. 107.
Видим, что поле ротора независимо от скольжения по отношению к неподвижному статору вращается с синхронной скоростью, а поле статора также вращается с синхронной скоростью по отношению к неподвижному статору. Поэтому в пространстве поле статора и ротора неподвижны между собой.
Рис. 107
Только при этом условии возможно взаимодействие и передача энергии от статора ротору. Ток ротора создает намагничивающую силу F2, по закону Ленца она направлена против намагничивающей силы статора.
При холостом ходе ток статора равен I0, но по мере нагрузки ЭДС Е2 растет, растет и ток I2, увеличивается F2 и поток ротора, который размагничивает поток статора, что приведет к уменьшению ЭДС Е1, и к увеличению тока статора I1, до такой величины, чтобы скомпенсировать размагничивающий поток ротора и обеспечить постоянство потока. Поэтому уравнение намагничивающих сил асинхронного двигателя будет аналогично трансформаторному 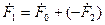
 2014-02-02
2014-02-02 1379
1379
