ПрограммированиеСБИС ПЛс использованием программатора
Программирование ПЛИС семейств МАХ9000, MAX7000S, МАХ7000А, МАХ7000 вне системы осуществляется с использованием программатора, выпускаемого фирмой Altera - Altera Stand Alone Programmer (ASAP2), который содержит:
1. логическую карту программатора - Logic Programmer card (LP6);
2. главный программирующий блок - Master Programming Unit (MPU);
3. адаптер, соответствующего типу корпуса СБИС.
Логическая карта программатора передает информацию о программировании и функциональном тестировании СБИС ПЛ из PC (MAX+PLUSII Programmer) в главный программирующий блок MPU. MPU совместно с адаптером, соответствующим типу корпуса, осуществляет тестирование и проверку запрограммированной микросхемы. Используемые при этом тестовые векторы могут быть созданы в редакторе временных диаграмм MAX+PLUSII Waveform Editor. Кроме того, MPU автоматически проверяет наличие электрических контактов между выводами микросхемы и разъемом адаптера, соответствующего типу корпуса ПЛИС.
Отметим, что СБИС семейств МАХ9000, MAX7000S, MAX 7000A, МАХ7000 обеспечивают внутреннее преобразование 5В питающего напряжения в 12В, требуемые для программирования (репрограммирования) EEPROM ячеек. Во время осуществления процедуры программирования (репрограммирования) выводы СБИС находятся в Z-состоянии.
Глава 5. Методы и средства функционального синтеза
Математические модели электронных схем. Анализ электронных схем на ЭВМ осуществляется с помощью математической модели, т.е. системы уравнений, описывающей работу исследуемой схемы. Математическая модель схемы (ММС) состоит из компонентных (макромодельных) и топологических уравнений. Компонентные уравнения — уравнения элементов или макромоделей. Топологические уравнения — уравнения связи элементов в узле или устройстве.
Переменные, характеризующие состояние элементов, принято называть фазовыми переменными. Обозначим: V — вектор фазовых переменных; E - подвектор, образованный фазовыми переменными вектора V, производные которых фигурируют в компонентных уравнениях. Для электронных схем V — вектор токов и напряжений всех ветвей схемы, E — индуктивные токи и емкостные напряжения.
При формировании ММС задается перечень элементов системы и имеется библиотека элементов или макромоделей, т.е. подсистема компонентных уравнений F(z,V,t)=0. После дискретизации уравнение будет иметь вид
Fk(zk, Vk, tk) =0, (2.1)
где zk=z(th), Vk=V(th), tk — значение независимой переменной t для k- гошага интегрирования. Выполнив разложение (2.1) в ряд Тейлора в окрестностях точки (z ki, V ki), являющейся i -м приближением к корню этой системы, и сохранив в разложении только линейные члены, получим
Аkizk,i+ 1 + BkiVk,i+1 = Q ki, (2.2)
где Aki =  Fk/
Fk/ zk , Bki =
zk , Bki =  Fk/
Fk/ Vk ивектор правых частей Qki определены в точках (zki, V ki), a (zk,i+1, Vk,i+1) — точки (i+1)-гo приближения к корню.
Vk ивектор правых частей Qki определены в точках (zki, V ki), a (zk,i+1, Vk,i+1) — точки (i+1)-гo приближения к корню.
Так как заданы межэлементные связи, то известна подсистема топологических уравнений
DVk,i+1 =0 (2.3)
где D — топологическая матрица.
Для полноты системы математической модели используется подсистема, выражающая формулу численного интегрирования:
F(zk,i+1,Vk,i+1)=0. (2.4)
Для большинства методов подсистема (2.4) линейна:
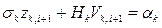 ,
,
и задача формирования ММС конкретизируется как задача формирования матриц 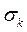 , Hk, D, Аki, Bki и векторов
, Hk, D, Аki, Bki и векторов 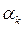 и Q ki.
и Q ki.
Общая система уравнения ММС:
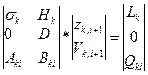
Подсистема линейных алгебраических уравнений (2.3) выражает законы Кирхгофа для токов и напряжений для выбранной совокупности независимых контуров и сечений в графе схемы замещения (эквивалентной схемы). Выбор совокупности эквивалентен выбору фундаментального дерева в графе схемы. Фундаментальным деревом связного графа называется суграф, в котором отсутствуют циклы. Для связного графа с а вершинами фундаментальное дерево состоит из 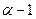 ребра. Нордами называются ребра, не вошедшие в фундаментальное дерево.
ребра. Нордами называются ребра, не вошедшие в фундаментальное дерево.
Система уравнений для первого закона Кирхгофа:
Jр + МJх = 0, (2.5)
Где Jp и Jx – векторы токов соответственно ребер и хорд фундаментального дерева; М — топологическая матрица контуров и сечений.
Система уравнений для второго закона Кирхгофа:
U x – MTU p = 0 (2.6)
где UX и Up — векторы напряжений соответственно хорд и ребер фундаментального дерева; Мт — транспонированная матрица М.
Следовательно, подсистема уравнений (2.3) с матрицей коэффициентов D принимает вид
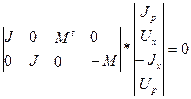
Операции выбора фундаментального дерева и формирования матрицы М формализованы.
В настоящее время для формирования системы уравнений применяются методы переменных состояния, метод узловых потенциалов, обобщенный метод и т.п. [16],
Метод переменных состояния (МПС). В методе переменных состояния в качестве переменных используются напряжения на емкостях и токи через индуктивности (переменные состояния). Метод основан на получении ММС в форме, удобной для применения явных методов численного интегрирования обыкновенных дифференциальных уравнений.
В МПС исходными являются уравнения:
J P + MJ X = 0;
UX - MUP = 0;
FK(zK,VK,tK) = 0;
где матрица М формируется на основе нормального дерева в графе схемы. Нормальным деревом графа схемы называется дерево, которое содержит все источники напряжения, максимально возможное число конденсаторов и резисторов, минимально возможное число индуктивностей.
В этом случае М-матрица имеет следующую структуру:
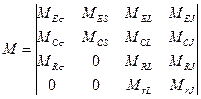
Здесь С, S — матрицы конденсаторов, попавших в дерево и хорды графа соответственно; R, 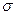 — матрицы резисторов, попавших в дерево и хорды графа соответственно; Г, L — матрицы индуктивностей, попавших в дерево и хорды графа соответственно. Зависимые и независимые источники напряжения Е, JE и источники тока J, UJ.
— матрицы резисторов, попавших в дерево и хорды графа соответственно; Г, L — матрицы индуктивностей, попавших в дерево и хорды графа соответственно. Зависимые и независимые источники напряжения Е, JE и источники тока J, UJ.
Тип ветви определяется видом соответствующего ей компонентного уравнения. В МПС предполагается, что компонентные уравнения резистивных ветвей связывают JR и UR, емкостных Ветвей Us и Js либо Uc и Jc, индуктивных ветвей JL и UL либо JГ и UГ; при этом в уравнениях связи могут фигурировать переменные состояния, к которым относятся Uc и JL. Источники напряжений Е и тока J могут быть независимыми или зависимыми только от переменных состояния и времени, т.е. компонентные уравнения имеют вид:
FR(UR,JR,UC,JL) = 0; (2.8)
Fr(Ur,Jr,UC,J L) = 0; (2.9)
FS(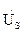 ,JS,UC J L) = 0; (2.10)
,JS,UC J L) = 0; (2.10)
FC(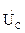 ,JC,UC J L) = 0; (2.11)
,JC,UC J L) = 0; (2.11)
FL(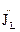 ,UL,UC J L) = 0 (2.12)
,UL,UC J L) = 0 (2.12)
Fr(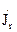 ,Ur,UC J L) = 0; (2.13)
,Ur,UC J L) = 0; (2.13)
FE(UE,Uc,J L, t) = 0; (2.14)
Fj(Jj,UC,J L, t) = 0. (2.15)
Математическая модель схемы ММС состоит из трех подсистем алгебраических уравнений и формул явного интегрирования обыкновенных дифференциальных уравнений. Первая подсистема формиру ется из линеаризованных уравнений (2.8), (2.9) и топологических уравнений, характеризующих резисторы:
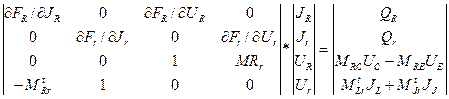
Вторая подсистема формируется из линеаризованных уравнений (2.11) и топологических уравнений, относящихся к матрице конденсаторов:
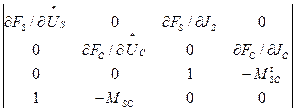 *
*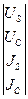 =
= 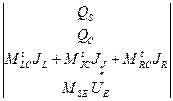
По аналогии формируется третья подсистема из линеаризованных уравнений (2.12), (2.13) и топологических уравнений, относящихся к индуктивностям:
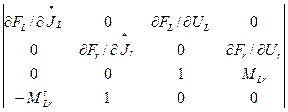 *
*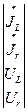 =
= 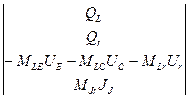
Здесь Qr, QR, Qs, Qc, QL, Qr — правые части линеаризованных компонентных уравнений, зависящие от переменных состояния:
Qr = -Fr(Ur,Jr,Uc,JL).+ ( Fr/
Fr/ Jr)J'r+(
Jr)J'r+( Fr/
Fr/ Ur)U'r;
Ur)U'r;
QR = -FR(U'R,J'R,UC,JL) + ( FR/
FR/ JR)J'R + (
JR)J'R + ( FR/
FR/ UR)U'R;
UR)U'R;
QS = - FS(U'SJ'S,UC,JL) + ( FS/
FS/ JS)U'S + (
JS)U'S + ( FS/
FS/ JS)J'S
JS)J'S
и т.д., где обозначение переменной со штрихом относит ее к предыдущей итерации вычислительного процесса,
Таким образом, на очередном шаге численного интегрирования обыкновенного дифференциального уравнения (ОДУ) явными методами выполняются следующие вычисления:
по известным от предыдущего шага значениям U c, JL и известному значению t вычисляются значения UE, JJ путем решения
компонентных уравнений (2.14) и (2.15) и значения их производных по времени;
вычисляются правые части и коэффициенты системы уравнений (2.16)...(2.18);
вычисляются векторы J R и U г по (2.16);
вычисляются векторы 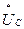 и
и 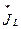 по (2.17);
по (2.17);
применяется одна из явных формул интегрирования, позволяющая по () U с и () J L вычислить значения 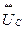 и
и 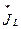 для нового шага интегрирования.
для нового шага интегрирования.
Метод позволяет использовать неявные методы интегрирования ОДУ. Рассмотренный метод переменных состояния отличается высо кой наглядностью, так как позволяет получить конечную форму математической модели схемы в виде дифференциального уравнения.
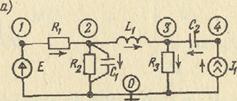
Пример. Построить ММС для схемы рис. 2.20, а, граф-схема которой приведен на рис. 2.20, б с помощью МПС в случае использования явных методов интегрирования.
|
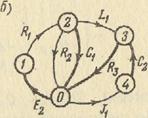
Рис. 2.20. Принципиальная (а) и граф-схема (б) устройства
Для рассматриваемого примера матрица М имеет вид
M = 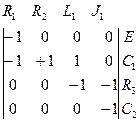
Математическая модель схемы представляется следующими тремя системами уравнений:
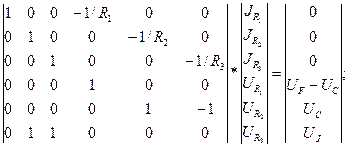
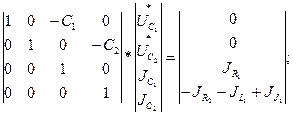
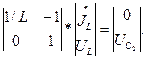
Реализация построенной ММС позволяет подобрать все значения компонентов схемы и провести оптимизацию исследуемой схемы.
Метод узловых потенциалов. В данном методе в качестве независимых переменных используются напряжения во внутренних узлах схемы относительно некоторого опорного узла, потенциал которого принимается равным нулю. Внутренним узлом называется узел, который не связан непосредственно с источником напряжения.
В основе метода лежит первый закон Кирхгофа. В методе узловых потенциалов (МУП) различают классический и модифицированный варианты. В классическом варианте вектор определенных переменных составляют узловые потенциалы, топологические уравнения которых представлены в виде
AJ -0, U + At 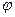 = 0, (2.19)
= 0, (2.19)
где J — вектор токов ветвей; 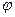 — вектор узловых потенциалов; А — матрица.
— вектор узловых потенциалов; А — матрица.
Для получения ММС используется процедура линеаризации и исключения небазисных координат. В результате ММС принимает
вид
Я V= Q, (2.20)
где Я — матрица узловых проводимостей, Q — вектор правых частей, V — вектор базисных координат.
Порядок системы равен 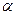 - 1, где
- 1, где 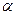 — количество узлов в схеме. Однако классический метод имеет ряд ограничений, в частности в нем недопустимы идеальные источники напряжения, индуктивности и т.п., поэтому в настоящее время используется модифицированный вариант МУП.
— количество узлов в схеме. Однако классический метод имеет ряд ограничений, в частности в нем недопустимы идеальные источники напряжения, индуктивности и т.п., поэтому в настоящее время используется модифицированный вариант МУП.
В этом методе ветви разделяются на особые и неособые. Особые ветви — ветви из идеальных источников напряжения, индуктивностей и ветви, токи которых являются управляющими у каких-либо других ветвей; все остальные ветви — неособые.
Вектор базисных координат состоит из вектора 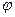 узловых потенциалов и вектора J 2 токов особых ветвей. Исходными являются уравнения (2.1) и (2.19), а также компонентные уравнения неособых ветвей
узловых потенциалов и вектора J 2 токов особых ветвей. Исходными являются уравнения (2.1) и (2.19), а также компонентные уравнения неособых ветвей
F1(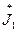 , J2,
, J2, 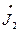 , U1,
, U1, 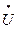 )=0
)=0
и особых ветвей
F2(J2, 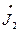 , U1,
, U1, 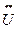 )=0,
)=0,
где 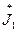 — вектор токов неособых ветвей.
— вектор токов неособых ветвей.
После линеаризации компонентных уравнений выполняется процедура исключения небазисных координат, в результате чего получается ММС
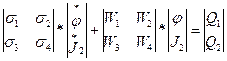 ,
,
где
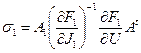 ,
, 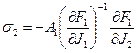 ,
,

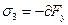 ;
;  ,
,  ;
;
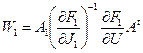 ,
, 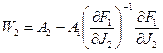 ;
;
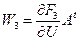 ,
, 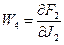 ;
;
A=[A1A2], A1 и A2 - матрицы инциденций узлов соответст венно с неособыми и особыми ветвями;
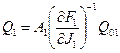 , Q2=Q02, Q01, Q02 - постоянные члены линеаризованных компонентных уравнений.
, Q2=Q02, Q01, Q02 - постоянные члены линеаризованных компонентных уравнений.
Модифицируемый метод предусматривает предварительную алгебраизацию дифференциальных уравнений на основе формул интегрирования Гира:
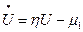 ,
, 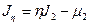 ,
,
где 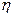 — коэффициент, зависящий от размера шага интегрирования, а векторы
— коэффициент, зависящий от размера шага интегрирования, а векторы 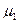 и
и 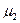 , кроме того, от значений фазовых координат U и J 2 на P -предшествующих шагах, где Р — порядок метода. Тогда ММС представляется как
, кроме того, от значений фазовых координат U и J 2 на P -предшествующих шагах, где Р — порядок метода. Тогда ММС представляется как
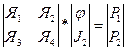 ,
,
где 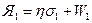 = A1D1At – матрица узловых проводимостей;
= A1D1At – матрица узловых проводимостей;
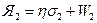 = A2-A1D2 –матрица безразмерных коэффициентов; Р1 =- A1D3, Я3,Я4 и Р 2 получаются на основании линеаризации компонентных уравнений:
= A2-A1D2 –матрица безразмерных коэффициентов; Р1 =- A1D3, Я3,Я4 и Р 2 получаются на основании линеаризации компонентных уравнений:
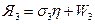 ;
; 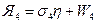 ;
;
P2 = -F2(J2, 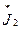 , U,
, U, 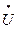 ) + (
) + ( F2/
F2/ J2)J2 + (
J2)J2 + ( F2/
F2/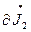 )
)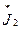 + (
+ ( F2/
F2/ U)U+(
U)U+( F2/
F2/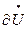 )
)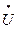 +(
+( F2/
F2/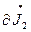 )
)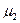 +(
+( F2/
F2/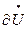 )
)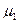 .
.
В определении матрицы Якоби участвуют матрицы D1, D2 и D3, которые определяются из выражений
D1 = ; D2 =
; D2 =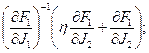
D3 = F1(J1J2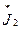 U1
U1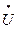 )+
)+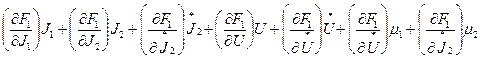 .
.
Все переменные Jl,J 2, U, 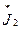 ,
,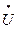 относятся к предыдущему шагу итерации.
относятся к предыдущему шагу итерации.
Алгоритм формирования матрицы  F /
F /  J и вектора J в общем случае включает последовательное обращение к математическим моделям всех компонентов схемы. Рассмотрим действия, которые производятся при обращении к модели k- гокомпонента, имеющего п выводов и подсоединенного к схеме с узлами j1...jn.
J и вектора J в общем случае включает последовательное обращение к математическим моделям всех компонентов схемы. Рассмотрим действия, которые производятся при обращении к модели k- гокомпонента, имеющего п выводов и подсоединенного к схеме с узлами j1...jn.
1. Вычисляются токи выводов компонента 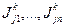 по аналитическим зависимостям, связывающим токи выводов и напряжений на выводах компонента.
по аналитическим зависимостям, связывающим токи выводов и напряжений на выводах компонента.
2. Токи выводов суммируются с соответствующими элементами вектора узловых токов:
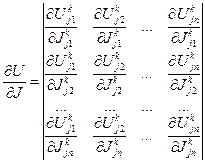 .
.
3. Вычисляются производные  на выводах компонента.
на выводах компонента.
4. Вычисленные производные суммируются с соответствующими элементами матрицы полных узловых проводимостей.
В результате реализации модели можно исследовать статические и динамические параметры схемы и определить коэффициенты чувствительности выходных параметров схемы к изменению ее входных параметров.
Метод многополюсных подсхем. Метод основан на разделении сложной схемы (или системы уравнений) на простые подсхемы (подсистемы) с учетом связей между ними.
Решение задачи высокой размерности сводится к последовательному или параллельному решению нескольких подзадач меньшей размерности.
Предполагается, что моделируемая схема разбита на k подсхем путем проведения сечений через схемные узлы. Каждый компонент схемы принадлежит одной подсхеме. Внутренние узлы пронумерованы в следующем порядке: внутренние узлы первой подсхемы {1,2,...,n}, внутренние узлы второй подсхемы { п 1+1, п 1+2,..., п 1+n2 } и т.д. Узлы межсвязей обозначим {N1+l, N1+2,..., Nl+m},где
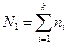 . Под узлами межсвязей подразумевается такие внутренние узлы схемы, которые образованы путем соединения компонентов схемы, принадлежащих разным подсхемам.
. Под узлами межсвязей подразумевается такие внутренние узлы схемы, которые образованы путем соединения компонентов схемы, принадлежащих разным подсхемам.
При такой нумерации узлов схемы структура матрицы проводимостей имеет вид
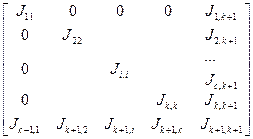 .
.
Подматрица Jii, имеющая размерность (ni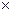 ni), является матрицей проводимостей i-й подсхемы, соответствующей внутренним узлам. Подматрицы Ji,k+1, Jk+1,i, Jk+1,k+1 размерностями (ni
ni), является матрицей проводимостей i-й подсхемы, соответствующей внутренним узлам. Подматрицы Ji,k+1, Jk+1,i, Jk+1,k+1 размерностями (ni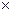 m), (m
m), (m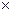 ni), (m
ni), (m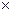
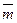 ) описывают взаимное соединение подсхем.
) описывают взаимное соединение подсхем.
Пусть U={ U1U2…Uk} — вектор потенциалов во внутренних узлах подсхем, V — вектор потенциалов узлов межсвязей.
ММС принимает следующий вид:
C1(U1,V) = 0;
C2(U2, V) = 0;
…
Ck(Uk,V) = 0;
F(U, V) = 0,
где С i = { gn i +1+1, g ni-1 +2,…, g n2} — вектор задающих токов для внутренних узлов i-й подсхемы; F= {f1,f2,…fm} — вектор задающих токов для узлов межсвязей. При этом переменные U1, U 2,…, UN являются функциями аргументов 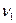 ,
,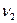 ,…,
,…,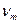 которые принимаются за независимые переменные:
которые принимаются за независимые переменные:
Uj = Uj( 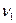 ,
,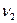 ,...,
,...,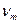 ), j=1,2,…N1.
), j=1,2,…N1.
Вектор задающих токов F представляется рядом Тейлора:
F=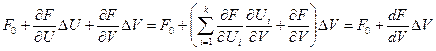 ,
,
Где 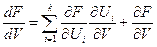 .
.
Таким образом, для вычисления 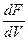 необходимо определить матрицы производных
необходимо определить матрицы производных 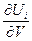 , i = 1,2,..., k.
, i = 1,2,..., k.
Рассматривая уравнения 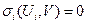 как неявное задание функции Ui, элементы матрицы
как неявное задание функции Ui, элементы матрицы 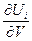 можно получить по правилу Крамера из системы линейных уравнений
можно получить по правилу Крамера из системы линейных уравнений
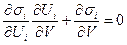 ,
,
откуда
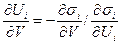 , i=1,2,…,k.
, i=1,2,…,k.
Вычислительный процесс строится таким образом, что решение системы трансцендентных уравнений высокого порядка, описывающей работу всей схемы, заменяется решением системы более низкого порядка, описывающей соединение подсхем в единую цепь. При этом на каждом шаге итерационного процесса для нахождения якобиана и вектора F0 необходимо решить k систем нелинейных уравнений соответствующих подсхем.
Метод диакоптики. В этом методе декомпозиция большой схемы на подсхемы производится путем проведения линий сечения через ветви, которые называют ветвями межсвязей. Под узлами межсвязей подразумеваются схемные узлы, к которым подключены ветви межсвязей.
Соотношения между узловыми напряжениями и узловыми токами описываются с помощью матриц проводимостей каждой подсхемы Ji,i; i = 1,2,,.,,k. Размерность матрицы Ji,i определяется суммарным количеством ni - внутренних узлов подсхемы и узлов межсвязей, принадлежащих данной подсхеме:
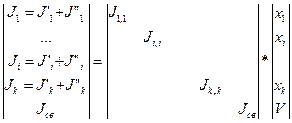 ,
,
где J'i - — вектор задающих токов i-й подсхемы без учета вектора J"i токов, обусловленного взаимным соединением подсхем; Jсв представляет собой матрицу проводимостей ветвей межсвязей размерностью (с 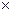 с); С — количество ветвей межсвязей; jсв — токи ветвей межсвязей; V — напряжения на ветвях межсвязей.
с); С — количество ветвей межсвязей; jсв — токи ветвей межсвязей; V — напряжения на ветвях межсвязей.
Вычислительный процесс по методу диакоптики строится по следующему алгоритму:
x0=J1-1J’; J”=-Cz4-1Cix0;
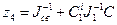 ; x(1)=
; x(1)=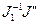 ;
;
x=x(0)+x(1).
В матрице С размерностью N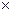 C строки соответствуют схемным узлам, а столбцы — ветвям межсвязей;
C строки соответствуют схемным узлам, а столбцы — ветвям межсвязей; 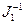 — обратная матрица.
— обратная матрица.
Диакоптические методы анализа больших интегральных систем (БИС) разделяются на две группы: раздельного итерирования и раздельного интегрирования.
Метод раздельного итерирования основан на использовании различной скорости сходимости итераций при решении нелинейных алгебраических уравнений для отдельных подсхем. Применение метода Ньютона на каждом шаге интегрирования системы приводит к одинаковому числу итераций для всех подсхем, которое определяется по подсхеме с наиболее медленной сходимостью итераций.
Метод раздельного интегрирования основан на различной инерционности отдельных подсхем, когда в одной подсхеме переходные процессы протекают быстро, а в другой — медленно. К методам раздельного интегрирования относятся методы учета латентности, вложенных шагов, однонаправленных реакций, прогнозируемых реакций [18, 19].
 2014-02-02
2014-02-02 625
625








